Download Neural Oscillations

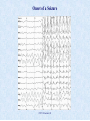
CN510: Principles and Methods of Cognitive and Neural
Modeling
Neural Oscillations
Lecture 24
Instructor: Anatoli Gorchetchnikov <[email protected]>
Teaching Fellow: Rob Law <[email protected]>
It Is Much Easier to Have Oscillations
CN 510 Lecture 24
Importance of Oscillating Models
It is much easier to have oscillations in the model than not to have
them:
– Delayed feedback inhibition is one of the main causes of
oscillations, and there is no instantaneous feedback in vivo
Oscillations allow to synchronize neurons across multiple brain
regions:
– Modulatory systems that set oscillatory patterns project to
many brain areas simultaneously
Oscillation-based models allow to consider individual spikes rather
than firing rates:
– Randomness is reduced or eliminated by synchronization
– Phase coding can be used in addition to rate coding
Last and most important: oscillations are present all over the brain,
we will not be able to model brain accurately without them
CN 510 Lecture 24
What Is Oscillation?
Neural network or neuron is said to be oscillatory if there is a
variable (membrane potential, Ca concentration, some current)
that is periodic with a well defined period
The system has to be stable to perturbations, meaning that it will
return to the original amplitude and frequency (period) with a
possible phase shift
The absence of this shift usually means that the perturbed network is
not the source of oscillation, but rather is driven by external
source
CN 510 Lecture 24
What Is Synchrony?
Neurons are essentially coincidence detectors
We talked about spatial and temporal summation of neuronal inputs:
signals have more effect on the membrane potential if they arrive
close in time
How close depends on the receptor we use: for AMPA simultaneous
means within 20ms, for NMDA within 300ms
Neurons below fire phase-locked to each other with 5ms delay, but
if our time resolution is 10ms, then they fire synchronously
CN 510 Lecture 12
Multiple Scales of Oscillations and Synchrony
Membrane potential oscillations in
individual cells (intracellular
recordings)
Local field potentials (extracellular
recordings,
EEG,
etc):
combined activity of many
cells, usually mixing individual
oscillations with network-driven
oscillations
CN 510 Lecture 24
Extracellular Recordings
What extracellular recordings actually record?
The current through the cell membrane consists of the capacitive
and resistive component
dV
Cm
  Ii
dt
i
dV
I m  Cm
 Ir
dt
From the extracellular point of view:
– If this current flow in the cell then it creates a current sink
– If it flows outside of the cell it creates the current source
in this particular part of the membrane
If the electrode is placed at a distance twice as large as the distance
between parts of the cell with major currents, then the field on
this electrode will be similar to the field generated by the current
dipole (Humphrey, 1979)
CN 510 Lecture 24
Extracellular Recordings
Assuming the extracellular fluid has constant conductance, the
potential on the electrode is
1  I m I m 
Ve 
  
4  r
r 
where
– I-s and r-s are currents and distances, respectively,
– + and – mark the attributes of source and sink, respectively,
– σ is the extracellular conductivity
Note, that currents have opposite signs: I+ is positive, while I- is
negative
Therefore, if r+ > r- then Ve < 0, and if r+ < r- then Ve > 0
CN 510 Lecture 24
Extracellular Recordings
In the case of more complex cell with many possible sources and
sinks
Ii
Ve 

4 i ri
1
Finally, for the continuous neuron the sum can be replaced with the
integral (Humphrey, 1979)
So extracellular recordings reflect the sum of all transmembrane
currents for all neurons in the vicinity of the electrode tip
weighted by the distances
CN 510 Lecture 24
Conditions for Simulation of LFP
Need to have sources and sinks: model neurons have to have at least
two compartments, otherwise by Kirchhoff's law the total current
is zero for each neuron
Need to have some spatial distribution of these neurons, otherwise
distances from the electrode are meaningless
How to measure a total current that goes across the membrane if
you have an arbitrary number of these currents?
dV
Cm
  I s   IV  I a  I g
dt
You can measure the currents that don’t go across: axial and gap
junctions only!
Note that both of these are computed from voltages:
g V i 1 (t )  V i (t )   g V i 1 (t )  V i (t ) 
so we can compute them off-line after the simulation is done!
CN 510 Lecture 24
SMART Diagram for LFP Simulation
CN 510 Lecture 23
Examples of Simulated LFP
CN 510 Lecture 24
Oscillations in Extracellular Recordings
CN 510 Lecture 24
EEG Frequency Bands
delta (1–4 Hz)
theta (4–8 Hz)
alpha (8–12 Hz)
beta (13–30 Hz)
gamma (30–70 Hz)
Note that these are human
frequencies, animals differ
slightly
CN 510 Lecture 12
Membrane Potential Oscillations
Many neurons produce rhythmic subthreshold membrane potential
oscillations
Intrinsic electrical properties of neurons, primarily voltage gated
channels lead to generation of these oscillations
The functional relevance of these oscillations is based on increased
and decreased excitability of the neuron and can lead to
noticeable firing changes:
– Giocomo et al (2008) found a gradient of properties of Ih
current in the entorhinal cells, which fit nicely into the
interference model of grid cells
Resonate-and-Fire neuronal model by Izhikevich is a simple
approach to modeling subthreshold oscillations
CN 510 Lecture 24
Membrane Potential Oscillations
Subthreshold oscillation frequency can vary, from few Hz to over
40Hz
They are often similar in frequency to LFP oscillations
Why is that?
CN 510 Lecture 24
Measuring Synchrony
Word of caution: certain number of synchronous events will always
happen by random coincidence
Need to compare to some non-zero baseline
– Calculate expected number of synchronous events based on
firing rates and interspike interval distributions, then calculate
the number of actual events and take the ratio as a measure of
synchrony
– Do spike shuffling: shuffle the spike train preserving firing
rates and interspike interval distributions and compare number
of events for unshuffled vs shuffled case
Advantage of this method comparing to correlation methods is that
synchronous events do not have to be reoccurring or periodic
CN 510 Lecture 23
Measuring Oscillations
Spike train autocorrelation:
– Align signal with itself, calculate correlation coefficient (gotta
get 1 here)
– Delay signal relative to itself by Δt, calculate correlation
coefficient again
– Repeat. You get a value for each Δt. Plot these values in a
histogram: autocorrelation histogram
Note that for autocorrelation the plot is symmetrical
White noise autocorrelation is flat
CN 510 Lecture 24
Measuring Oscillations
Similar technique can be used
for LFPs
You can also compare different
signals
by
building
crosscorrelation diagram
CN 510 Lecture 24
Measuring Oscillations and Synchrony
Two aperiodic and synchronous signals will have a single peak at
zero
Two aperiodic phase-locked signals will have single peak shifted
from zero
Two periodic synchronous signals will have wavy crosscorrelogram
if their frequencies are similar: the further away the frequencies
the faster the waviness will decay
Two periodic phase-locked signals will have wavy
crosscorrelogram with peak shifted from zero
CN 510 Lecture 12
What Causes Oscillations?
In the individual neuron any kind of delayed inhibitory feedback
will lead to oscillations:
– In Hodgkin-Huxley there is a fast Na and slow K currents
– Adding more currents with different time courses will
manipulate the frequency
Similar, in the network any kind of delayed interactions will also
lead to oscillations
– Delayed inhibition in RCF leads to oscillation
– Delayed excitation can also lead to oscillatory patterns, but
most of the time there is some form of inhibition that does the
job
Combining individually oscillating neurons into a feedback network
leads to most interesting oscillatory patterns
You can overlay neuromodulation on top to further regulate the
dynamics
CN 510 Lecture 24
Interactions Between Delay, Oscillations, and Synchrony
Conductance delays in the brain lead to oscillatory patterns
Cells within or across brain areas synchronize despite these delays
In the 90-es Nancy Kopell and Bard Ermentrout looked in detail on
how conductance delays interact with oscillations and can lead to
synchrony
Another group that looked at the similar issues were Eugene
Izhikevich and Frank Hoppensteadt
CN 510 Lecture 24
Neuronal Types
Type I:
– Based on saddle-node bifurcation
– All-or-none action potential
– Long latency to fire after transient stimulus
– Square root or linear FI curve (firing rate from input current)
– Arbitrary long oscillation period
Type II:
– Based on Hopf bifurcation
– Graded action potential amplitude
– Limited range of frequencies
– Short firing latencies
CN 510 Lecture 24
Weakly-coupled Systems
Only timing of firing is changed by inputs
Approximate the system (neuron) by a periodic function and
analyze interactions between these functions
Most of the analysis deals with phase shifts of the oscillators
For Type I neurons:
– If coupled with inhibition at low frequencies both
synchronous and anti-phase solutions are stable, at high
frequency only the synchronous one is stable
– If coupled with excitation – synchrony is stable at low
frequencies, anti-phase at high frequencies
More on these systems in Izhikevich (2006) and his references
CN 510 Lecture 24
Strongly-coupled Systems
Inputs can make neuron fire but do not influence the next oscillation
cycle
Reduction of the system to a map (Ermentrout and Kopell, 1998)
Example of a system:
E-I circuit is an oscillator:
– tonically active E cell drives I cell that
spikes only once
– I cell spikes sufficiently fast to prevent a
second E spike until the inhibition wears
off
– inhibition recovery time constant sets the
frequency of this oscillation (realistic
GABAA leads to γ frequencies)
CN 510 Lecture 24
Strongly-coupled Systems
Conductance delay in cross-circuit connections is
– slower than I recovery period, so I will fire one spike in
response to local excitation and another for remote excitation
if both E cells spike simultaneously
– faster than wearing off of the inhibition, so this second I spike
will arrive at local E cell before it recovers from the first spike
So basically the circuit can be fully symmetric
with E cells firing synchronously at a
frequency that is determined by four
inhibitory events:
–
–
–
–
Local I spike in response to local E spike
Local I spike in response to remote E spike
Remote I spike in response to remote E spike
Remote I spike in response to local E spike
CN 510 Lecture 24
Strongly-coupled Systems
From the circuit E&K proceed to map representation in terms of
spike timings and derive a map function F in terms of time
difference between two E spikes Δ and the conduction delay δ
This function was analyzed for stability of oscillations for a
complete system as well as for system with E-to-I or I-to-E cross
circuit projections removed
Network with both projections synchronizes over larger range of
conductance delays and does it faster than network with just Eto-I projections
CN 510 Lecture 24
Strongly-coupled Systems
There are two independent effects in the model
– The response of the inhibitory (I) cells to excitation from
more than one local circuit
– The response of the excitatory (E) cells to the multiple
inhibitory spikes they receive
Together, they give the network synchronization properties that are
not intuitively clear from the properties of either alone
– For the weaker cross-circuit E-I coupling the synchrony fails
if the delay in these projections is too small
– Reducing the I refractory periods or increasing cross-circuit
I-E coupling reduces the minimal delay needed for stability
CN 510 Lecture 24
Strongly-coupled Systems
In the network with no I-to-E cross-circuit projections: E cells
receive only local inhibition (two spikes instead of four)
– Here the timing of I spikes does not affect the range of delays
over which the synchrony is stable
– System in general is more tricky and can have some weird
aperiodic or high frequency solutions
– On the other hand non-homogeneous networks synchronize
faster and better with just E-to-I projections
Network with just I-to-E cross-circuit projections: I cells fire single
spikes rather then doublets, so E cells again receive two I spikes
– Synchrony is always stable
– Can also form stable anti-phase solution
To prove that map reduction works they also ran full scale
simulations with the same results
CN 510 Lecture 24
Slow Coupling
Coupling is strong and slow so that inputs can make neuron fire on
a different oscillation cycle
Coupled leaky integrate-and-fire behave similar to coupled
conductance based (HH-style) Type I neurons
– Slow inhibition or fast excitation is beneficial for
synchronizing neurons
– Fast inhibition or slow excitation is beneficial for locking
them in anti-phase
Izhikevich proved that for one parameter regime the system of
identical slow coupled oscillators converges to stable oscillations
independently of the sign of projections, but the convergence to
this state is oscillatory by itself:
– Phase difference oscillates on its way to 0
For a different parameter setting the phase difference can oscillate
indefinitely (converges to a limit cycle)
CN 510 Lecture 24
Example of Simple Cases
Two identical integrate-and-fire neurons will
– Synchronize when coupled through inhibitory connections
– Phase-lock in anti-phase when coupled with excitatory
connections
CN 510 Lecture 24
What Drives You?
Three regimes of network oscillations:
Tonic – when period of oscillation is small comparing to membrane
and synaptic time constants; here the oscillation is driven by
some fast network interactions and both membrane constant and
inhibition work like damping
Phasic – when membrane constant is short comparing to the period
of oscillation and synaptic constant; here synaptic activity drives
the frequency
Fast – when synaptic constant is short comparing to period and
membrane constant; here membrane properties drive the
frequency
It is especially important to know these when you attempt to
synchronize a heterogeneous network
CN 510 Lecture 24
What Is the Function of Oscillations?
Is there a function?
Some people believe that oscillations per se have a stabilizing
function
Others believe that interplay between different oscillations leads to
some interesting effects (interference model of grid cells)
Yet others believe that oscillations that we observe are just a
byproduct of neuronal activity, which also leads to all effects
attributed to oscillations
Suggestion:
If you model a structure that is a source of a certain oscillation then
make sure that these oscillations are created by your network in
the process of solving whatever task you model
CN 510 Lecture 24
Brief Summary
Research on oscillations and synchrony addresses two main
questions: function and mechanism
It is not clear to date if oscillations are a necessary byproduct of
neural interactions, or if they serve a specific function
More is known about how oscillations arise in neural circuits; in
fact, it seems quite difficult not to have oscillations to emerge
when neurons are connected together
Oscillations are not always a sign of healthy brain function, indeed,
when oscillations become dominant one can often see seizures
during which large areas of the brain oscillate together in an
undamped fashion
CN 510 Lecture 24
Onset of a Seizure
CN 510 Lecture 24
Next Time
Rob’s lecture
CN 510 Lecture 24