Download “Electrical Properties of Neuron”

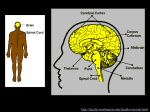
“Electrical Properties of Neuron”
Learning Objectives
At the end of the lecture,



Student should be able to understand the morphology of neuron and its basic
physical and electrical properties.
Students should also be able to appreciate the mechanics of action potential
initiation and measurements of action potentials.
The basics of patch-clamp technique should also be introduced.
Lecture Outline
Morphology of Nerve cells (The Neuron):
• Dendrites -- Input
• Cell body (soma) -- Integration
• Axon – Output.
Structure of neurons – Dendrites:
•
At dendrites, the neurons recieve input via axons of other neurons at synapses.
Structure of neurons – Soma:
In the soma of the cells, the cell nucleus is located (containing the DNA, i.e. genetic
code); the synthesis of the proteins (within ribosomes and endoplasmatic reticulum) as
well as energy production (mitochondria) are performed.
Structure of neurons – Axon:
The axon transmits the information electrically from the soma to the synapses –
It is surrounded by myelin that insulates the axon, provided by oligodendrocytes (glial
cells).
Electrical properties of neurons:
 Neurons are enclosed by a membrane separating interior from extra cellular space
 The concentration of ions inside is different (more –ve) to that in the surrounding
liquid.
 -ve ions therefore build up on the inside surface of the membrane and an equal
amount of +ve ions build up on the outside
 The difference in concentration generates an electrical potential (membrane
potential) which plays an important role in neuronal dynamics.
 Cell membrane: 2-3 nm thick and is impermeable to most charged molecules and
so acts as a capacitor by separating the charges lying on either side of the
membrane.
 NB Capacitors, store charge across an insulating medium. Don’t allow current to
flow across, but charge can be redistributed on each side leading to current flow.
 The ion channels are proteins in the membrane, which lower the effective
membrane resistance by a factor of 10,000 (depending on density, type etc)
Excitation and Conduction:
 Most biological neurons communicate by short electrical pulses called action
potentials or spikes or nerve impulses
 These action potentials are generated by means of influx and out flux of ions
through the ion channels embedded in membrane
 Suitable electrical probe (electrode) and measurement instrumentation (amplifier
and read-out) can measure these tiny potentials on the order of few milli-volts
 Nerve cells have a low threshold for excitation – may easily be excited by
electrical, chemical or mechanical stimuli
 Two types of physiochemical disturbances are produced as a result
 Local or Non-Propagated Potentials such as Synaptic, Generator or Electrotonic
Potentials.
 Propagated Disturbances such as Action Potentials or Nerve Impulses
The Patch-Clamp Technique:
 This is a novel technique (developed by Neher and Sakmann et al. for which they
were awarded with a Nobel prize) in which physiological currents flowing
through the cells can be detected without disrupting the cell or its contents
 A micropipette (diameter in microns) filled with a buffer solution and carrying a
metal electrode is gently touched to the cell membrane and the membrane
contents are sucked in, forming a giga-seal. This is called a patch-clamp. Because
of high resistance, very small currents (pico-Ampere, 10E-12A) corresponding to
ion channel movements can be measured, with the help of Ohm’s law.
Advanced Topics:




Membrane Capacitance, Membrane Current and Membrane Resistance
Biophysical Models of the Neuron
The Integrate-and-Fire Model
The Hodgkin-Huxley Model
Membrane Capacitance and Resistance:
 Most channels are highly selective for a particular type of ion
 Capacity of channels to conduct ions can be modified by eg membrane potential
(voltage dependent), internal concentration of intracellular messengers (Cadependent) or external conc. Of neurotransmitters/neuromodulators
 k Also have ion pumps which expend energy to maintain the differences in
concentrations inside and outside
 Exterior potential defined to be 0 (by convention). Because of excess –ve ions
inside, resting membrane potential V (when neuron is inactive) is –ve

 G Resting potential is the equilibrium point when ion flow into the cell is matched
by ion flow out of cell

 V will vary at different places within the neuron (eg soma and dendrite) due to the
different morphological properties (mainly the radius)
 Neurons without many long narrow cable segments have relatively uniform
membrane potentials: they are electrotonically compact
 Start by modelling these neurons with assumption that membrane potential is
constant: single compartment model
 Denoting membrane capacitance by Cm and the excess charge on the membrane
as Q we have:
Q = CmV and dQ/dt = CmdV/dt
 Shows how much current needed to change membrane potential at a given rate
 Membrane also has a resistance: Rm Determines size of potential difference
caused by input of current: IeRm
 Both Rm and Cm are dependent on surface area of membrane A.
 Therefore define size-independent versions, specific membrane conductance Cm
and specific membrane resistance Rm
 Membrane time constant tm = RmCm sets the basic time-scale for changes in the
membrane potential (typically between 10 and 100ms)
The Nernst Equation and Equilibrium Potential
 Potential difference between outside and inside attracts +ve ions in and repels –ve
ions out
 Difference in concentration between inside and outside mean ions diffuse through
channels (Na+ and Ca2+ come in while K+ goes out)
 Define equilibrium potential E for a channel as membrane potential at which
current flow due to electric forces cancels diffusive flow
 Eg Consider +ve ion and –ve membrane potential V: V opposes ion flow out, so
only those with enough thermal energy can cross the barrier so at equilibrium get:






[outside] = [inside] exp(zE/VT)
Z - is no. of extra protons of ion
VT - is a constant (from thermal energy of ions)
E - is equilibrium potential
Solve to get the Nernst Equation:
 From Nernst equation get equilibrium potentials of channels:EK is typically
between –70 and –90 mV, ENa is 50mV or higher, Eca is around 150mV while
Ecl is about 65mV (near resting potential of many neurons)
 A conductance with an equilibrium potential E tends to move membrane potential
V towards E eg if V > EK K ions will flow out of neuron and so hyper polarise it
 Conversely, as Na and Ca have +ve E’s normally V < E and so ions flow in and
depolarise neuron
Membrane current:
 The membrane current is total current flowing through all the ion channels
 We represent it by I m which is current/unit area of membrane
 Jj Amount of current flowing through each channel is equal to driving force (the
difference between equilibrium potential Ei and membrane potential) multiplied
by channel conductance gi
Therefore:
im = gi(V - Ei)
 Conductance change over time leading to complex neuronal dynamics.
 However have some constant factors (eg current from pumps) which are grouped
together as a leakage current.
 Over line on g shows that it is constant. Thus it is often called a passive
conductance while others termed active conductances
 Equilibrium current is not based on any specific ion but used as a free parameter
to make resting potential of the model neuron match the one being studied
 Similarly, conductance is adjusted to match the membrane conductance at rest
This leads to the prediction that the firing rate is a linear function of current (fig A
above).
However, while the model fits data from the inter-spike intervals from the first 2
spikes well, it cannot match the spike rate adaptation which occurs in real neurons
For this to occur, we need to add an active conductance (fig C)
Biophysical Models:
 Although many crucial properties of real neuron remain unknown, biophysical
model incorporate some known properties of neural tissue
 Like real, spiking neurons these models produce spikes rather than continuous
valued outputs
 Integrate – and – Fire Model
 The Hodgkin – Huxley Model
Integrate and Fire Model:
 Divides membrane behavior conceptually into two regimes.
 A prolonged period of linear “integration”
 A sudden “firing”
 Relaxes the requirements that a single set of continuous differential equations
describe the cell’s two very different regimes.
 Easily implement using simple electronic circuits.
The Hodgkin – Huxley Model:
 Biophysically much more accurate single cell models that can account for the
very complex, non stationary behavior of real neurons
 The dynamics are modeled by numerous coupled ,nonlinear differential equations
that describe the behavior of continuous currents that depend in a nonlinear
manner on the membrane potential
 Although this model is powerful, if suffers from the drawback that it requires
detail knowledge of a myriad of parameters. It is frequently difficult to properly
constrain all these degrees of freedom.