Download Cell Assemblies - CAAM @ Rice

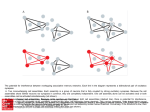
Understanding a Cell Assembly Down to its Core
Karina Aliaga, Department of Mathematical Sciences, New Jersey Institute of Technology
Tyler Young, Department of Bioengineering, Rice University
Dr. Steve Cox, Department of Computational and Applied Mathematics, Rice University
Dr. Illya Hicks, Department of Computational and Applied Mathematics, Rice University
Cell Assemblies and Graph Theory
Introduction
Ever since psychologists and neuroscientists began studying the
physiological inner workings of the brain, they have been puzzled by many
questions. How are concepts stored and recalled within our brains? How does
learning and memory occur? In 1949, D.O. Hebb tried to explain the answers to
these questions in terms of cell assemblies in his book The Organization of
Behavior. Hebb asserts that a cell assembly is a group of neurons wired in a
specific manner such that when a sufficient amount of neurons in this group are
excited, the entire group becomes excited in a synchronized manner. Hebb went
on to explain that these cell assemblies form via synaptic plasticity. He claims that
if neuron A repeatedly fires neuron B, some metabolic activity occurs increasing
the efficiency in which neuron A fires neuron B making it easier for neuron A to fire
neuron B. This phenomenon is more commonly known as “cells that fire together,
wire together.” Hebb postulates that the ignition of a series of these groups of
neurons, or cell assemblies, can explain how concepts are stored and recalled
within our brains, thus allowing learning and memory to occur.
-cores: a concept that many graph theorist have been
studying since the 1970’s. A -core can be defined as:
Given graph X, the subset X is a _-core if every
node in _ has at least _ neighbors in X _ .
Minimal _-core:
If no proper subset of the _-core is also a _-core,
then it is minimal.
Examples
2
Closure:
1
3
(1) Create : we will use the minimal 2-core found by
previous example
5
4
2
3
1
4
6
Cell Assemblies and k-cores
(2) Find
in the
5
:
One type of cell assembly, we will call a -assembly, is the closure of a minimal core. In order to find these -assemblies, we needed to develop a method for finding
minimal -cores and their closures in any given network of neurons.
Research Goal
Algorithms
Our research goal is to understand cell assemblies and to develop a method
for finding them within any given network of neurons. This will allow us to better
understand and explain the inner workings of our brains.
Finding minimal _-cores:
MATLAB has a built-in function (________) that finds an optimal solution to
binary integer programming problems of the following form:
Because
we must apply
again:
minimizes the objective function:
________ arguments:
: Coefficients of the variables of the objective function
:
Using the threshold inequality we can find _ _:
Applying
again will generate an invariant set because the whole
graph is excited, thus giving us the closure of , a - assembly.
Cell Assemblies: A Different Perspective
G. Palm: Towards a Theory of Cell Assemblies. Biological Cybernetics.181-193
(1981), was the first to give a mathematical definition of cell assemblies.
Let
be a graph with a set of vertices
Adjacency Matrix (
and edges
)
A matrix of binary elements representing the connectivity of a network of
neurons such that if_______ __ there exists a connection between neurons
and _ . Conversely, if
___then no connection between neurons _
and _ exists.
Finding _-assemblies:
______
minimizes __ constrained to ______. Because
satisfies the inequality, we must add an additional constraint.
_
Threshold ( )
The minimum number of inputs a neuron needs in order to become excited
Closure :The invariant set generated by
Let
be a subgraph in
.
.
Conclusion
Examples
is a binary vector representing the presence ( ) or absence ( ) of a neuron
2
3
1
4
6
A set is invariant if:
5
In this example,
finds the minimal 2-core
. There are, however,
many other minimal 2-cores in this set of neurons such as
,
and
`
. Our goal for the future is to find some method that enables ______ to find
all of the minimal -cores in a given network thus, allowing us to find all of the assemblies in that network.
Working on this project, we have extended Palm’s Mathematical definition of cell
assemblies to fit a binary integer programming problem. Also, we created a link
between the world of graph theory and cell assemblies: the closure of a minimal
_-core is a - assembly. Lastly, we created an algorithm that allows us to find at
least one cell assembly in any given network of neurons.
Acknowledgements
This work was supported by a NSF REU Grant DMS-0755294 and
NSF VIGRE Grant DMS-0240058. We would like to thank Dr. Cox and
Dr. Hicks for their guidance throughout this project. Lastly, we would
like to thank Diane Taylor and Shaunak Das, our research collaborators.