* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download IV. Model Application: the UAV Autonomous Learning in Unknown
Artificial neural network wikipedia , lookup
Cognitive neuroscience of music wikipedia , lookup
Neural coding wikipedia , lookup
Convolutional neural network wikipedia , lookup
Molecular neuroscience wikipedia , lookup
Clinical neurochemistry wikipedia , lookup
Brain Rules wikipedia , lookup
Biology and consumer behaviour wikipedia , lookup
Limbic system wikipedia , lookup
Neuropsychopharmacology wikipedia , lookup
Eyeblink conditioning wikipedia , lookup
Machine learning wikipedia , lookup
Embodied cognitive science wikipedia , lookup
Premovement neuronal activity wikipedia , lookup
Concept learning wikipedia , lookup
Catastrophic interference wikipedia , lookup
Mathematical model wikipedia , lookup
Neural modeling fields wikipedia , lookup
Orbitofrontal cortex wikipedia , lookup
Neuroeconomics wikipedia , lookup
Metastability in the brain wikipedia , lookup
Recurrent neural network wikipedia , lookup
Biological neuron model wikipedia , lookup
Holonomic brain theory wikipedia , lookup
Types of artificial neural networks wikipedia , lookup
Synaptic gating wikipedia , lookup
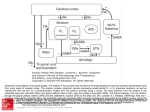
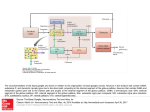
Cogn Comput 1 A Basal Ganglia Network Centric Autonomous Learning Model and Its Application in Unmanned Aerial Vehicle Author identifying information Conflict of Interest: Yi Zeng declares that he has no conflict of interest. Guixiang Wang declares that she has no conflict of interest. Bo Xu declares that he has no conflict of interest. Cogn Comput 2 A Basal Ganglia Network Centric Autonomous Learning Model and Its Application in Unmanned Aerial Vehicle Yi Zeng · Guixiang Wang · Bo Xu Abstract Autonomous learning paradigms bring flexibility and generality for machine learning, while most of them are mathematical optimization driven approaches, and lack of cognitive evidence. In order to provide a more cognitive driven foundation, in this paper, we develop a basal ganglia network centric autonomous learning model. Compared to existing work on modeling basal ganglia, the work in this paper is unique from the following perspective: (1) Our work takes the orbitofrontal cortex (OFC) into the consideration. The orbitofrontal cortex is critical in decision making because of its responsibility for reward representation and is critical in control of the learning process, while most of the basal ganglia models do not include the orbitofrontal cortex; (2) To compensate the inaccurate memory of numeric values, a method called precise encoding is proposed in this paper to help the working memory remember most of important values during the learning process. The method combines vector convolution and the idea of storage by digit bit and is efficient for accurate value storage; (3) In the information coding process, the Hodgkin-Huxley model is used to obtain a more biological plausible description of action potential with plenty of ionic activities. To validate the effectiveness of the proposed model, we apply our basal ganglia network centric autonomous learning model to the Unmanned Aerial Vehicle (UAV) autonomous learning process in a 3D environment. We build the state, action and reward space for the UAV in the environment. Experimental results show that our model is able to give the UAV the ability of free exploration in the environment after an average of 41 trainings. Keywords autonomous learning model · basal ganglia network · precise encoding · UAV autonomous learning · reinforcement learning · interactive environment. Yi Zeng(*) · Bo Xu Institute of Automation, Chinese Academy of Science, Beijing, 100190, China, and CAS Center for Excellence in Brain Science and Intelligence Technology, Chinese Academy of Sciences, Shanghai, 200031, China email: [email protected] Guixiang Wang Institute of Automation, Chinese Academy of Science, Beijing, 100190, China email: [email protected] The first and the second authors contributed equally to this work, and serve as co-first authors. I. Introduction Human brains are general information processing systems with high intelligence and creativity, and can deal with various and complex cognitive tasks. This is what traditional artificial intelligence lacks and should be inspired from. Brain-inspired neural networks have attracted more and more attention in recent years since they provide new opportunities to achieve the goal of General Intelligence. The neural network architecture of the brain supports the realization of cognitive behaviors at multiple scales. Although spiking neural networks have been adopted for cognitive behavior simulation and creating intelligent applications [7, 11, 20], they are generally considered to get inspirations from the brain at microscopic scale. While in most models, macroscopic inspiration, which emphasize on the coordination mechanisms of different brain regions are missing, especially for computational learning model. In this paper, we propose a basal ganglia centric computational model for autonomous learning, and we provide applications of the proposed model in the autonomous learning process of the Unmanned Aerial Vehicle (UAV). In hundreds of brain areas, the basal ganglia (BG) play a central role in cognition and are related to the realization of various cognitive functions such as action selection and reinforcement learning [1-4, 6]. The basal ganglia do not perform these cognitive tasks alone. When selecting actions or performing a reinforcement learning task, the basal ganglia need to work together with their main input from the cortex and main output to the thalamus [34]. Actually, the basal ganglia are associated with wide areas of the cortex [11], which receives output of the basal ganglia via thalamus [5, 8, 9, 11], forming the cortex-basal ganglia-thalamus loop. In this paper, we name this loop the basal ganglia circuitry. The Basal ganglia are a set of highly interconnected subcortical nuclei located in the midbrain, around the thalamus [4, 6]. Basal ganglia are implicated in diverse functions [5], among which, action selection and reward-based learning get more attention in recent years [1-4, 6, 17]. These two processes are closely related to reinforcement learning. In the learning process, the basal ganglia itself is a modulatory system, modulated by dopamine (DA). Dopamine dynamically modulates activity in the basal ganglia and controls learning process [4, 5]. Damaging to the basal ganglia will cause the reduction of releasing dopamine, which leads to cognitive Cogn Comput 3 deficits such as Parkinson’s disease (PD) [8, 10]. This indicates the key influence of basal ganglia on human cognition. The cognition study on the basal ganglia circuitry has produced a variety of models. The “box and arrow” model [18, 19] is an earlier and ordinary description of the basal ganglia based on anatomical data. Following this previous study, complicated basal ganglia models [8, 10, 12, 17, 19, 20] are developed, by adding additional connections among nuclei or more areas in the basal ganglia circuitry. They are built using artificial neural network [8, 12, 19], conductance-based biological neuron models [17] or spiking neural networks [20]. While there still need some improvements in these models. Most of the basal ganglia models are built using artificial neural network, which cannot give a good description on neural activities; ionic level neuron model is not used in these basal ganglia models; they usually do not take all the important brain regions into account, especially the orbitofrontal cortex (OFC); they do not have a real memory for precise value storage. Besides, the problem these models can handle is easier than the real situation. Based on the unsolved issues above, we propose our basal ganglia model with several major contributions listed below. Firstly, the Hodgkin-Huxley (H-H) model [28, 29] is applied in our model to build the basal ganglia network. It has more ionic dynamics than other models such as the leaky integrate-and-fire (LIF) model and can make better predictions on neural activity [30]. Changes in ionic conductance of sodium (Na+) and potassium (k+) will influence cognition process. Simulations about the ionic channel of the H-H model can provide a better explanation about the influence on cognition. Secondly, the orbitofrontal cortex (OFC) is taken into account while most of the basal ganglia models didn’t consider this. The orbitofrontal cortex (OFC) is a part of the prefrontal cortex (PFC) [34] and is associated with reward information representation [8, 21, 22] in decision-making and reinforcement learning. A more comprehensive basal ganglia model including the OFC and the amygdala is developed in this paper. The OFC in our model receives the relative magnitude of reinforcement values from amygdala [22] and represent gain-loss information in the memory, including positive reward and punishment. As the modulatory effect of the dopamine (DA), the OFC modulates both the basal ganglia and the PFC [22] and is a critical brain area in reinforcement learning. Thirdly, a precise encoding mechanism base on working memory is proposed in this paper. The PFC undertakes the task of working memory to store values and parameters in reinforcement learning process [3, 4, 8]. The working memory achieved in [4, 14] cannot remember precise values, while many values need to be remembered precisely like human does. Our method of precise encoding handles this problem well. Q-values, rewards, and other important values associated with reinforcement learning process are stored in memory using the precise encoding mechanism. Q-values in this paper are state-action matrix included from reinforcement learning [2, 34, 39]. The sate-action pairs are used for action-selection. An action is chosen when it has high Q-values than others in a given state. Last but not least, unlike most of the cognitive experiments, which deal with relatively simple decision-making task [1, 4, 8], our model’s application of UAV autonomous learning in 3D environment is more complicated and full of realistic significance. Intelligent agents are expected to help people with repeated or dangerous tasks [43, 44]. The latter is what we concern more about. In recent years, brain-inspired models are applied to decision-making process and many are associated with the basal ganglia [4, 8, 17, 39, 40]. The study in [17] developed a basal ganglia model to control a robot’s action selection on the ground. Another robotic basal ganglia model [41] for the simulation of rat food search is built, also in 2D ground. Different from simpler action selections in 2D space, we make our application in 3D environment with more complicated realistic task and the environment remains unknown to the UAV during the learning process. An unknown 3D environment’s complexity lies in several aspects. (1) Agents in a 3D environment have more freedom and also more action probabilities; it’s harder to train an agent in these scenes. (2) The environment is unknown means the UAV knows nothing about the terrain, the mountains and when and where the enemies come out. It only knows the distances to other nearby objects. (3) To get a better learning result, the number of states for UAVs to feel nearby objects is large (hundreds of states), and this means complex situation and long training process. The rest of this paper is organized as follows. Section II gives a detailed description of the basal ganglia from the anatomy perspective to the mathematical model perspective. Section III is our methods, including the Hodgkin-Huxley model for information coding; the precise encoding algorithm we propose; our model of basal ganglia network based autonomous learning model with the consideration of the orbitofrontal cortex and the working memory. The application of the UAV autonomous learning under the basal ganglia network is presented in Section IV. Section V presents our experimental validations. Finally, Section VI concludes the paper and discusses the future work. II. Problem Statement and Previous Work A. The Problem What we are concerned about is building a brain-inspired cognitive model, which achieves intellectual behavior using important brain structures and connections. Brain-inspired model is another way to reach human-like intelligence. With the brain as an anatomical instructor, this kind of model has several benefits for the intelligence research. (1) The brain is the source that generates the intelligence; and Cogn Comput 4 studying brain-structure-based model helps exploring the origin of the intelligence. One can develop the function of specific brain structures and validate them using computing algorithms or observed data from brain. This will benefit disease researches associated with the brain and also brain machine interface. (2) It will contribute to the study of biological mechanisms. There are many neural evolution and communicating rules in the brain, such as the spike timing-dependent plasticity (STDP) [2]. Experimental results on the brain-inspired models are much easier to observe than that from real brains. And this will help analyzing the relations between neuron activities and biological rules. (3) Brain-inspired models are built using spiking neural network, in which the spike is a strong information-coding unit. Information is also encoded by spikes within brains. This information coding way enables the comparability from the neural-activity level between brains and brain-inspired models; and will facilitate the fusion of information got from different sense organs to form the whole brain model. Biological brain is so magical and intelligent so that we can get some inspirations from its biological structures and mechanisms. The basal ganglia in the brain are critical in cognitive behaviors such as action selecting and reinforcement learning. Many computing models are put forward based on the structure and function of the basal ganglia as well as their associated brain regions [8, 10-13, 17, 19, 20]. Most of these models are not comprehensive in brain regions and can only deal with sample action-selecting tasks. Besides, they pay less attention on more real and ionic neuron model such as the Hodgkin-Huxley model. In this paper, we build a more brain like basal ganglia model, with more brain regions and more real neuron model. We will explain our basic idea in the following and finally use this model in a 3D unknown environment to train an unmanned aerial vehicle (UAV). Our work is related with a basal ganglia model with mathematical description for action selection [13] and its expanded rate neuron model [1, 11]. We develop our own basal ganglia model based on this rate model because of several advantages. (1) The rate neuron model has low computational complexity and keeps main biological characters about the basal ganglia. Different biological neural models are available for the model. (2) The model’s activities usually correlate well to the activities in rat’s basal ganglia. (3) Besides, the model can deal with wide range of inputs with hundreds of dimensions [1]. These advantages facilitate the implementation of complex reinforcement learning process with spiking neural network. The application for UAV behavioral learning in this article needs hundreds of states, and the range of Q-values may vary in a wide range. Before the description of our model, we should introduce some basic models we used. B. The Neuroanatomy of the Basal Ganglia Fig. 2. Mathematical computing model of the basal ganglia (the cortex is not Fig. 1. The of the ganglia [9]. Note that the the thalamus and shown) [1]. neuroanatomy The input vector of basal the basal ganglia is from cortex (more the prefrontalthe cortex (PFC)cortex). are not the thevbasal ganglia. and D2 are specifically prefrontal x, y,parts z, uofand denote vectorD1 outputs from two receptors in The the striatum. = the globus GPi eachdopamine nucleus respectively. values inGPe the equations arepallidus from theexternal, mathematic = the internal globus pallidus, the subthalamic nucleus, SNc = the the model of the basal ganglia [1]. STN These=values in the equations make sure substantia nigra pars compacta, SNr = the substantia nigra pars reticulate. basal ganglia’s behavior is consistent with biological function. The basic components of the basal ganglia include striatum, the subthalamic nucleus (STN), the globus pallidus external (GPe), two output nuclei (the substantia nigra pars reticulata (SNr) and the internal globus pallidus (GPi) [4, 8-11]. Other nuclei, namely the substantia nigra pars compacta (SNc) and the ventral tegmental area (VTA), are also seen as part of the basal ganglia. The SNc and VTA release important modulatory signals named dopamine (DA), which are critical for several cognitive behaviors [5, 8, 10]. Major anatomical structures and components of the basal ganglia are provided in Fig. 1. The striatum is comprised of two nuclei, the caudate and putamen, which are functionally similar and often seen as two independent regions. Anatomically and functionally, these two components have connections with different basal ganglia regions, forming the direct pathway and indirect pathway. Striatum receives direct input from cortical areas and modulatory afferents (DA) from SNc. There are two types of DA receptors in striatum, D1 and D2. D1 receptor may enhance response of striatum neurons in the direct pathway, while D2 has the opposite function in the indirect pathway [8, 34]. The STN is also an input nucleus as it receives input from the cortex. It also receives inhibitory afferents from the GPe and projects excitatory efferent back to it. In addition, the STN also projects to the GPe and SNr, and excites both of them. The globus pallidus (GP) is composed of two nuclei, GPe and GPi. The GPe receives inhibitory afferent from the striatum, excitatory afferent from the STN, and has inhibitory connections with the STN and the GPi. The GPi is the output nuclei of basal ganglia. It receives inhibitory input from the striatum, the GPe and excitatory input from the STN. The GPi provides inhibitory output to the thalamus and the brainstem [10]. SNc and VTA are regions that release dopamine (DA) to control response intensity of striatum. As is mentioned before, Cogn Comput 5 the D1 and D2 receptor receive DA and have opposite effects on the striatum neurons. The basal ganglia are associated with wide areas of cortex [11]. In cognition process, the basal ganglia circuitry includes the cortex and the thalamus. The basal ganglia receive input from the prefrontal cortex and send their output to the thalamus [34], which project output of the basal ganglia back to the cortex [5, 8, 9, 11]. The basal ganglia circuitry has two different pathways, the direct pathway and the indirect pathway. In the direct pathway, excitatory input goes from the cortex to the D1 receptor and is projected to the GPi/SNc directly, while the indirect pathway goes from the D2 receptor to the GPi/SNc via relays in the GPe and STN [4, 10, 11]. C. The Rate Coding Model of the Basal Ganglia Before description of our basal ganglia model, we firstly introduce the mathematical model of basal ganglia proposed by Gurney et al [1, 4, 13]. The selection mechanism of each nucleus in the basal ganglia can be described as a linear equation [13]: ì 0 ï f (xi ) = í m(xi - ei ) ï 1 î xi < ei ei £ xi < 1 / m + ei (1) xi > 1 / m + ei where f (xi ) is the output of a nucleus with xi the input and 0 £ xi £ 1 a suitable value interval. The equation takes excited and inhibitory connection into account and distinguishes them with positive and negative moduli respectively. The exact equations for all five nuclei are shown in Fig. 2. The D1 and D2 receptor in the striatum receive inputs from the cortex and scale them with respective coefficients. Since D1 excites input from the cortex and D2 has an inhibitory effect on it, D1 has a scaling factor greater than 1 and D2 has a scaling factor less than 1. The input of the basal ganglia is usually a vector. Each value in the vector represents an action, and the basal ganglia should select one action according to these values. Every region in the basal ganglia is a group of neurons. Each group of neuron represents a vector. x, y, z, u and v denote vector outputs from each nucleus respectively. Note that these vectors have the same dimension with the input vector. The mathematical equations in Fig. 2 are from the model proposed in by Gurney [13]. The basic mission of the basal ganglia is to select an action according to a set of input values. The output of the basal ganglia should be close to zero for the action selected and positive for other actions [1, 11, 13]. Here, larger value is more likely to be selected. Given an input of [0.4,0.6,0.1] (the value’s interval is [0, 1]), the second value is much larger than Fig. 3. Firing rate curve of the Hodgkin-Huxley model under the various of current inputs. In our experiments, the neuron starts to have stable regular spikes when the current input is more than 7.5uA/cm2. The resting potential is set to 0 and the initial values of V, m, n, and h are set to 0. The time constant is 0.01ms. Simulation period is 1s. others and will be picked up by the basal ganglia. Since the output of the basal ganglia is inhibitory, the selected action will have value close to zero, and an output of [0.2,0,0.4] may be the response of the basal ganglia. In the following, we will show how this mathematical model be simulated by neuron spike coding mechanism. It is generally believed that biological neurons carry information by producing complex spike sequences [1, 14, 26]. These spikes encode input stimulus as firing rates, which gives a glance of neuron activities [23, 26]. The firing frequency increases as the enhancement of the input stimulus. With its robustness against noise especially ‘ISI’ noise, firing rate coding is applied in many biological neural studies [1, 4, 8, 11, 24, 26]. Suppose that J(x) is the current input, a function of x(t) , and G(x) is a neuron model (more specifically, we use here the H-H model). The membrane action potential of the neuron i can be written as: vi (t) = Gi (Ji (x(t))) (2) where vi (t) is the action potential of a neuron. The action potential of is pushed higher by the current input over time, and fires when reach the threshold. The spiking output of neuron i is denoted by: d (t) = Gi (Ji (x(t))) (3) and its firing rate is written as [14, 16]: ri ( x) hi (t )* i (t t j ) (4) j where hi (t) is the post-synaptic currents function with a time constant denoted by t PSC , and written as [1, 16]: hi (t) = e-t/t PSC (5) Cogn Comput 6 Equation (5) indicates that the effect of a neuron decays over time. After the encoding process, we need a decoding operation to get what we estimate, according to the given function f (x(t)). We can estimate the decoding output using the least-squared-error method [1, 11, 16] or other linear decoders such as Kalman filter [25]. Here we use the least-squared-error calculation. The estimated output can be expressed as: cognition. The Changes on the ionic conductance in sodium or potassium channel may affect the decision making or learning process, thus gives us an opportunity to investigate on our intelligence deep into the ion level. Thirdly, H-H model may give a more biological plausible simulation and prediction on neuron activity due to its predictive power and reproduction of all the critical biophysical properties of the action potential. The H-H model is represented as four equations [29]: N f ( x) ri ( x)di (10) (6) i where d i denotes the linear decoders and N denotes the number of neurons used to encode the input stimulus. The deviation between the estimated value and the input can be written as E [( f ( x) f ( x))]2 dx (7) Through minimizing the deviation E, we obtain the least-squared version estimation of the decoder di : N arg min [( f ( x) ri ( x)di )]2 dx di (8) i For a continuous input x, it is given by [1, 11]: d = G -1¡ G ij = ò ri rj dx ¡ i = ò ri f (x)dx (9) In our basal ganglia computational model, the Hodgkin-Huxley model is used for information coding in the algorithm provided above. The decoders d and the firing rate ri are composed of the weights between two groups of neurons. Learning is a process that updates these synaptic weights using error signal, which will be explained in Section IV. III. Methods A. The Hodgkin-Huxley Model The Hodgkin-Huxley (H-H) model provides a good description of action potential for neurons in the ionic level [28, 29]. It is used to substitute G(x) in Equation (2). There are three reasons for using H-H model [28, 29] in this paper. Firstly, H-H equations give more description in the ionic level of the action potential using a coupled set of differential equations, which explains experimental results accurately and enables quantitatively voltage analysis on the nerve cell. Secondly, sodium and potassium are associated to human In the H-H model, V is the membrane potential, C is the membrane capacitance with a value C 1 F / cm 2 and I is the externally current input. The ionic current consists of three components, the sodium (Na+) current with three activation gates and one inactivation gate, the potassium (K+) with four activation gates, and the leak current carried primarily by chlorine (Cl-) [27, 30]. n , m and h in the equations represent the open probability of different ionic gates respectively [30], with n for potassium (K+), m and h for sodium (Na+). The transition rates of the gate between open and closed state are denoted by a (V ) and b (V ) , which are voltage-dependent [27, 30] and named rate constant. The transition rate functions are fitted by the voltage clamp experiments [29, 30]: 10 - V 10 - V exp( ) -1 10 25 - V a m (V ) = 0.1 25 - V exp( )-1 10 -V a h (V ) = 0.07 exp( ) 20 a n (V ) = 0.01 b n (V ) = 0.125 exp( b m (V ) = 4 exp( b h (V ) = -V ) 80 -V ) 18 (11) 1 30 - V exp( )+1 10 Note that the coefficients (0.01, 0.1, 0.007, etc.) in equation 11 are obtained by data fitting according to the H-H model experiments [29, 30]. They take these values because these values can give the best-fit curves. In order to set the resting potential V = Vrest = 0 , other potential and conductance values have been shifted and given the values [27, 31, 33]: EK 12 mV g K 36 mS / cm ENa 120 mV 2 g Na 120 mS / cm EL 10.6 mV 2 g L 0.3 mS / cm 2 Cogn Comput 7 where the three potentials are the equilibrium potential when the applied current I = 0 m A / cm2 and result in the resting potential V Vrest 0 . When the input current is larger than a specific value Iq , which is about 6 - 7 m A / cm2 in our simulations, regular spiking activity is observed [31]. If the spike interval is T , the average firing rate can be expressed as f = 1/ T , and it increases as the stimulus enhanced [31-33], but nonlinear, as shown in Fig. 3. Neurons in a group may have different firing or refractory times. Because the H-H model generates spikes regularly when the input current is large enough, we add an action potential resetting to it to control its firing process. The peak potential is about 80-100 mV when H-H fires, so we count a spike if the potential exceeds 60 mV and set the voltage to zero to let it restart right now or wait for a while before the finishing of the refractory. B. The Orbitofrontal Cortex in the Autonomous Learning Model The orbitofrontal cortex (OFC) is part of the prefrontal cortex (PFC) (see Fig. 4) and also participates in the reinforcement learning process [8, 21, 22]. It represents the reward information received from the amygdala [22] and gives a control on the basal ganglia model in the learning process. The OFC has connections with both the prefrontal cortex (PFC) and the striatum [22, 42] of the basal ganglia. The OFC modulates the striatum as the dopamine (DA) does. We suggest that this kind of modulation can be modeled by the synaptic weights between the PFC and the striatum. The OFC represents both positive and negative rewards in two separate sub-areas with functional distinction. These two sub-areas are the medial and lateral OFC respectively [21, 22]. Studies in [21, 22] show that the medial OFC tends to respond to positive reward of reinforcement values, whereas the lateral OFC is more active when representing negative rewards. That means, in our basal ganglia model, the medial OFC output a big respond value when a positive reward is received, and the lateral OFC gives a strong response when gets a negative reward. Note that strong response means large output value. Before modeling the contribution of the OFC, we need to explain general learning process in the basal ganglia network. Learning in our basal ganglia model is achieved by the updating of the synaptic connections between the basal ganglia and prefrontal cortex [1, 2]. As discussed above, the SNc/VTA area modulates the striatum (both StrD1 and StrD2) by releasing dopamine (DA), controlling the learning process. The response of striatum to the prefrontal cortex is modeled by the synaptic connections between them and is modulated by the learning errors (DA). Driven by learning errors, the synaptic weight change is written as [16]: Fig. 4. The basal ganglia circuitry after the consideration of the orbitofrontal cortex (OFC) and the amygdala. The prefrontal cortex (PFC) includes the OFC, which receives reward information from the amygdala. The thalamus here projects the output result of the basal ganglia back to the PFC, which is the working memory. Both the OFC and the SNc have the function of learning control for the basal ganglia. wij j di e j Eerr (12) where k is the learning rate. The influence of the OFC can be modeled in the synaptic learning rule (equation (12)). Rewrite the rule after taking the effect of the OFC: wij j di e j Eerr (1 ( p n )) (13) where m p is the medial OFC response and mn is the lateral OFC response with the value interval 0 £ m p , mn £ 1. Eerr is the error obtained from the Q-learning process and is given by [38, 40]: (14) Eerr = Rt (st ,at ) + g max Qt-1 (st ,a) - Qt-1 (st-1,at-1 ) a where g is discount rate and Rt (st ,at ) is the reward. The Q value function is updated by [38]: Qt (st ,at ) = Qt-1 (st ,at ) + r Eerr (15) where r is the learning rate in reinforcement learning. The incorporation of the OFC and the amygdala produces a more comprehensive basal ganglia circuitry. Also, The PFC is used as working memory. When performing reinforcement learning, the basal ganglia take the Q-values as input from the prefrontal cortex (PFC), and then output a selected action. A new precise coding method based on the working memory is proposed in the following to store accurate numeric values. Cogn Comput 8 Fig. 5. The target vector list and the key vector list for precise encoding. The target vectors represent elements including 10 Arabic numbers and one decimal point. There are 7 key vectors, representing 7 positions. The x-axis denotes serial number of every value in a vector. The y-axis represents value’s range (0,1). C. Precise Encoding for the Working Memory The problem In the reinforcement learning process, there are some state-action values ( Q(s,a) ), reward scores, parameters and errors have to be stored and updated while necessary. It is widely recognized that the prefrontal cortex (PFC) works as a working memory [3, 4, 8, 14, 15]. It stores values and parameters during learning process and updates them while necessary. When the environment’s current state is determined, the Q values of that state are extracted from the working memory and sent into the basal ganglia. Working memory mechanism can be achieved by integration, which connects the output of a population of neurons back to themselves to keep the information. Details about the integration implementation will not described here. With the help of the bind and unbind process [4, 14], which encode cognition process into vector-based descriptions using convolution, information at different times or with different meanings can be stored in one group of neurons together. If we want to remember a target in the memory, we need to assign a key to that target, and remember the convolution of the target and the key. When extracting the target from the memory, the key is used to distinguish which target is the right one, also by convolution. Binding (denoted by Ä ) is the storing process and unbinding (also Ä ) is the extracting process. They are all convolution process. Given two vectors A and B , the binding can be written as [4, 14]: (16) Fig. 8. The basal ganglia network built in this paper. When performing reinforcement learning, both the SNc and the OFC receives the reward information and control the synaptic weights updating between the striatum and the The OFC isofalso usedcoding as a working for value andthe reward Fig.PFC. 6. An example precise processmemory for the value ‘3.12’. final storing. result is sent into the working memory (the PFC). When given the binding position sequence in order, the number for every position is extracted. where FA e FB calculates the element wise product of the two vectors, and F is the discrete Fourier transform matrix. Unbinding process extracts the target input vector from the output (which is an approximate inverse of binding [14]). Given vector B, unbinding will get A by the equation [4, 14]: A » (A Ä B)Ä B¢ (17) where Bi¢ = B(N-i)mod N and it’s a permutation, knowing that the unbinding result is just a approximation of the original input. Note that the dimension of the vectors for both binding and unbinding must be the same. Because of the inaccuracy of the unbinding process, we cannot extract a value in the working memory without any deviation. This kind of memory is not good for accurate values (such as value of 3.12). The reason is that the coding and decoding process of the convolution will result in a not accurate reconstruction of the input. The error makes accurate representations of a value impossible. While we human can usually remember a value exactly without any deviation. And we do need this ability in many cases. Basic idea To improve this inaccurate memory, we develop an information encoding method called precise encoding, which is able to store accurate values in the working memory. The main idea of our method is dividing a value into units and remembering every unit. In the memory, if we want to get the target vector A , we need the key vector B . However, it is not possible to assign a key vector for every numerical value. Fortunately, the Arabic numbers are finite and only ten, if include the decimal point, that’s eleven. We assign a random target vector for every Cogn Comput 9 product [14] give matching scores between the extracted vector (take two for example) and those target vectors, and tell us what target (here include 10 numbers and one decimal point) it actually represents. Note that the dot product of two vectors is normalized by their length, written as: (a,b) (20) sv = ab And the larger score is the better. D. The Basal Ganglia Autonomous Learning Model Fig. 7. The function of working memory in the OFC. the working memory supports all the parameter storing during the learning process of the basal ganglia network. The working memory is achieved using the precise encoding method proposed in this paper. Arabic numbers including the decimal point, making sure that the dimension of the vector should not be too low (low dimension has less distinction and will cause confusion when calculate the similarity, for example, 32 is an available choice). Six significant digits will be reserved in our calculation, and that means seven positions (include the position of the decimal point) will be used. The target vector and key vector list is shown in Fig. 5. Note that the position numbers are in ascending order, from 0 for the least significant digit to 6 for the most significant digit. Seven randomly generated key vectors represent these positions respectively. That means for any given numeric value, we keep it in the working memory using six digits and one decimal point (if necessary). If a value has more than six digits, it will be cut off and kept the six top digits. While if less than six digits, the top digits will be zeros until a non-zero digit appears. Fig. 6 shows the encoding process of our method. Let’s take the value of 3.12 for example. It only has three significant digits and changing it into 0003.12 is the first step. After that, its binding result can be expressed as: M = two Ä P0 + one Ä P1 + dot Ä P2 + three Ä P3 + zero Ä P4 + zero Ä P5 + zero Ä P6 (18) and is sent into the working memory. When extracting the value from the memory, we should calculate the unbinding result from position P0 to P6 . For example, if we want the value in position P0 , we execute the unbinding process by the equation: (19) where P0¢ is the permutation of P0 , and P0 Ä P0¢ » 1 . After extracting the target vector, the similarities calculated by dot Our basal ganglia network model is shown in Fig. 8 and it is more comprehensive. (1) Our model includes the orbitofrontal cortex (OFC) for rewards response. The OFC is considered in our model to describe the reinforcement influence on the learning process. The OFC receives the reward information from the amygdala, controls the basal ganglia activities at the same time. (2) The model stores values and parameters using a working memory built by precise encoding algorithm we proposed. During the learning process, the basal ganglia and other brain regions interact with the PFC to store or take values when needed, as shown in Fig. 7. Every part in the model takes its own responsibility. The PFC is the working memory, storing all the parameters, function values, errors and rewards using precise coding algorithm. Every step, the PFC sends the value function to the basal ganglia according to current state. The basal ganglia are responsible for action selecting and sent its selection to the thalamus. The thalamus is a relay for signals in decision-making task, and sends the basal ganglia’s output back to the PFC. The SNc/VTA receives the error and rewards information and modulates the synaptic weights between basal ganglia and the PFC and learning begins, as shown in Fig. 8. Our basal ganglia network is built using H-H model. The whole model is a learning loop. Learning will not finish until the basal ganglia getting good action selections. There are two pathways in the circuitry (direct and indirect pathways). IV. Model Application: the UAV Autonomous Learning in Unknown 3D Environment A. The UAV’s Coordinate System and Distance Measurement The UAV (unmanned aerial vehicle) learns and behaves in an unknown 3D environment, so it is much important to give a brief and efficient description of the environment. Distance to other object is one of the most important information. The UAV should avoid collision without manual control when flying among mountains or buildings. With the help of distance Cogn Comput 10 Fig. 10. The staring points (red dots) and the probing directions in the horizontal plane. Here degree of 10 is just a typical value. sensors, which measure the distance between UAV and Fig. Theworld process of statessystem generation. horizontal and vertical state Fig.12. 9. The coordinate and theA:UAV body coordinate system. division. state examples for the UAV in an Note thatB:the moving direction is opposite to 3D the environment. z axis. through the UAV from head to tail and is in the opposite direction of flight (see Fig. 9). The horizontal plane determined by the x and z axes is divided into different directions by the detecting rays every f Fig. 11. A: Starting points for collision detection. B: The starting points (red dots) and probing directions in the vertical plane. obstacles from different directions, the UAV has the ability to perform auto avoidance. Precise distance is not a critical requirement for obstacle avoidance, so distance sensors such as lasers or ultrasonic sensors are available for the UAV [35, 37]. Distance within a few hundred meters is what we care about. We also need to know the UAV’s altitude, position and posture angles, which can be obtained using altimeter, GPS and gyroscope respectively. Two coordinate systems are considered in a 3D environment, the world coordinate system (wcs) and the UAV body coordinate system, as shown in Fig. 9. The world coordinate system is seen as a global coordinate system and defines the coordinates of every object in the environment, including the centroid position of the UAV. The body coordinate system is fixed on the UAV with the origin at its centroid and used to represent the orientation (posture angles) of the UAV body. In the body coordinate system, the vertical axis is y with positive direction going upward; the longitudinal axis (positive direction is from the head to the tail) is z; the lateral axis is x with positive direction pointing to the right, as shown in Fig. 9. The UAV is free to rotate in three dimensions. They are, pitch, head up or down about axis x, yaw, body left or right about axis y, and roll, body rotation about axis z. The z-axis passes degree around the UAV body ( is a typical value, same in the vertical plane, as shown in Fig. 10 and Fig. 11). These detecting rays are used to obtain distances from the UAV to the environment from different directions. The starting points of the rays are at the edges around the UAV body, as shown in red dots in Fig. 10 and Fig. 11. The positions of the starting point (the position of sensors) will be changed as the moving of the UAV. And there will be new probing directions as the posture changing of the UAV. All these changes have to be updated in order to get correct distance detection. Equations (21) and (22) do the adaption every time if there is a changing in position or posture of the UAV. æ cosq ( x ¢p , z ¢p , y ¢p ) = (cx ,cz ,cy ) + (x, z, y) ç sin q ç è 0 æ cosq ( xd¢ , zd¢ , yd¢ ) = (x, z, y) ç sinq ç è 0 - sinq cosq 0 - sinq cosq 0 0 0 1 0 0 1 ö ÷ ÷ ø ö ÷ (21) ÷ ø (22) Equation (21) updates the position of a starting point and equation (22) updates the probing direction of a starting point, so that every time the UAV changes its position or direction, new positions and probing direction of starting points will be calculated. B. The State and Action Space Taking for example, the horizontal and vertical planes are divided into 36 different directions by detecting rays. Distances got from these directions have different importance Cogn Comput 11 TABLE 1. TYPICAL REWARD VALUES FOR STATE CONVERSIONS State Conversion Reward Values for Reference ‘NoDange’ to ‘avoiding’ ‘NoDange’ to ‘NoDange’ -0.5 0.0 ‘avoiding’ to ‘NoDanger’ ‘avoiding’ less danger to ‘avoiding more danger ‘avoiding’ more danger to ‘avoiding’ less danger ‘avoiding’ to ‘avoiding’, same state ‘avoiding’ to ‘collision’ 1.0 -0.5 0.5 -0.5 -10 according to the angles between these detecting rays and also the flight direction. The state space, including both horizontal and vertical states, is obtained according to the degree of detecting ray in horizontal and vertical plane respectively. Supposing the state amount for the horizontal and vertical plane is N h and N v respectively, it means the horizontal plane can be divided into N h states with every state in a range of 360/ N h degrees, and it’s the same with the vertical plane. This kind of state generation is shown in Fig. 12. If the UAV is in state or , it means that there are obstacles in that direction. Given two thresholds D L and D S for the distance, take horizontal plane for example, when distances reported by all states are above D L , the UAV is in the state of ‘NoDanger’ , and given the state sh = 0 ; when distances reported by one or several states are below D L and none is below D S , the UAV is in the ‘avoiding’ state , and needs to take actions to avoid collision. When the distances from one or several states are below D S , the UAV is in the state of ‘collision’ and given sh = -1 . For the vertical plane, it’s the same. Knowing that there is a ‘NoDanger’ state for the horizontal and vertical plane respectively, and the UAV is in the ‘collision’ state if sh = -1 or sv = -1 , so we totally have the environment in order to get reward and update the basal ganglia model. C. The Reward Space The reward space is determined by a set of discrete values (typical values are shown in Table 1). Being no target point to reach, the purpose of UAV training is to avoid collisions while randomly wandering in the environment and the heading direction is random. Staying always in the state of ‘NoDanger’ will not get more positive reward, while a conversion from ‘avoiding’ state to ‘NoDanger’ state dose. The ‘NoDanger’ state is no harm to the UAV, and staying in it will get a reward value of 0. An action makes the state of the UAV change from ‘NoDanger’ to ‘avoiding’ will get a negative value and from ‘avoiding’ to ‘collision’ will get a larger negative reward. The amount of ‘avoiding’ states for the horizontal and vertical plane are N h and N v respectively. These states have different degrees of danger. The state whose direction is closer to the flight direction has a higher risk to collide and is more dangerous. This means the conversion from a state with lower risk to the one with higher risk gets a negative reward, on the contrary, positive reward. Table I is a typical value for reward in our training process. We give discrete reward values for state conversions in stable 1, while values that reflect these differences in state conversions are also appropriate (for example, linear function of those discrete values in table 1). The conversion from ‘avoiding’ to ‘avoiding’ is divided into three different cases. From state of ‘avoiding’ with less danger to ‘avoiding’ with more danger will get a negative reward value, in the opposite case, positive value. If the UAV stays in the same state of ‘avoiding’, a negative reward will be given (see table 1). Whenever the UAV collides an obstacle, it will get a larger negative reward value, because collision is much worse than other states. NS = (Nh +1)*(Nv +1) +1 states. V. Experiments Every time, every state reports a distance from the UAV to the environment. The state generation process (Fig. 12) may takes several detecting rays as a state if the range of degree (such as 36) of a state is larger than the range (such as 10) of a detecting ray. The distance reported by a state is the smallest one got from all the detecting rays belonging to that state. There is no kinematic and dynamic model in the UAV’s training process. Controlling a mathematical model of the UAV is not the purpose of this paper. Therefore, the action space of the UAV is simplified into 5 actions. They are (1) forward, (2) left and forward, (3) right and forward, (4) upward, (5) downward. We define l s as a linear moving step (include Based on the unknown 3D environment built in section IV, we apply our basal ganglia network for the UAV training process. In the environment, the UAV should wander around (random moving direction) and learn to avoid both static and moving obstacles. Important values (such as Q-values, rewards) for the learning process are stored in the working memory using the precise encoding. Every step, the environment is evaluated and its state is identified. The basal ganglia circuitry takes Q-values as input and selects one action as its output. And the UAV will perform the action just selected. According to the reward got from the OFC and state-action pairs just visited, the error and reward information are sent into the SNc. The Dopamine will control the learning process and help updating the synaptic weights. This is the learning process. forward, upward and downward) and J s as a rotating angle step (such as turn left or right, usually 30 degrees). Every time, the UAV chooses an action before moving a step, and detects Cogn Comput 12 Fig. 13. The experiment of precise encoding process. A: the input vector and memory result. The vector in the memory is a temporal addition result. B: the output vector and extracted value. The key vector comes at time of 180ms and the extraction begins at that time. Note that the extracted target vector is not exactly the former input vector but an approximating result. The decimal point is represented by the value of ‘-1’ here. Fig. 14. The accuracy experiments of precise encoding. 20 experiments are carried out in order to test the accuracy of the method. In every experiment, 100 values are generated randomly in range of (0, 100000), and are stored and extracted using the precise encoding method. The results show that the accuracies are above 0.9 and the average accuracy is around 0.95. A. The Precise Encoding Fig. 13 shows the precise encoding result of the value of 3.12 and the simulation lasts for 400 milliseconds (ms). The dimension of the target and key vectors is 100 here. In the experiments, a vector with 100 dimensions gets a good distinction among vectors that represent different elements (Arabic numbers or positions), as shown in Fig. 13. As explained in the precise encoding in section IV, ‘3.12’ is first changed into ‘0003.12’. Remember that the encoding Fig. 15. The action selection experiment on the basal ganglia. The top figure is the input action list. There are five actions and their value will change every 100 ms. The basal ganglia need to select the action with biggest value. Note that the output of the basal ganglia is negative. The basal ganglia select an action by outputting it’s value closed to zero. begins with the least significant digit (‘2’) until the most significant digit (‘0’) and there is 7 positions totally including the decimal point. The memory will remember a number with right position within 20ms. Part A in Fig. 13 shows the target and key vector inputs and the memory result when remembering ‘3.12’. After the value encoding is finished at time of 140ms, the memory will remember the value for a long time to wait for the extraction. Figure B shows the extraction process of ‘3.12’ from the memory. The extracting signal comes at time of 180ms and the extraction begins with also the least significant digit (‘2’). In order to identify the decimal point, we assign a value of -1 for it. As shown in B (Fig. 13), the extraction goes position by position. As a result of similarity calculation (equation (20)), Cogn Comput 13 Fig. 18. Attempt accounts before the success of the learning. 21 experimtns are included; and 1000 steps without collision indicates the finishing of learning. Fig. 16. 3D environment for the UAV autonomous learning. The environment is unknown to the UAV. Fig. 17. The simulation of the enemy UAV. The enemy can emerge at any direction and a certain distance from the UAV. the value ‘3.12’ is recognized (‘-1’ for the decimal point) correctly. Note that the extraction should begin after the finishing of the memory process. B. H-H Based Basal Ganglia Action Selection In this paper, we use the Hodgkin-Huxley (H-H) model for basal ganglia network implementation. Fig. 15 is a simulation of basal ganglia action selecting using the H-H model. It should be noted that the output of the basal ganglia is inhibitory. The basal ganglia select one action by output a nearly zero response. In Fig. 14, there are five actions. Each time period (about 100 millisecond), the basal ganglia should select one from them. As explained in section II, a action which has big value is better. So, the basal ganglia take five actions with different values as inputs and select the one with big value by output an nearly zero value. C. UAV Autonomous Learning We develop our 3D UAV training environment using jMonkeyEngine [36], which is a 3D game development kit written in Java. After the basic scene construction (such as the 3D environment, the UAV model), we define available actions for the UAV and abstract states according to the distances between UAV and environment objects, as analyzed in section V. With proper reward scores (table I), under the control of the basal ganglia network, the UAV can learn how to wander in the environment without collision with other objects. The learning environment developed by us is shown in Fig. 16, with a main view of first-person and four small views from other perspectives (third-person view, left view, right view and rear view). The mountain and terrain are unknown to the UAV and what we get is the distance from the UAV to the environment from many directions. Five actions are available here for the UAV and Every time, if no obstacles, the UAV will choose moving directions randomly. There are also moving obstacles in the environment as the enemy UAV. Fig. 17 shows the emergency of the enemy from different directions. Actually, the moving direction of the enemy can be any one from the circle around the UAV. In this kind of 3D unknown environment with static and moving obstacles, the UAV’s ‘inner brain’ learns how to interact with the environment to avoid collisions. Connection weights of neurons update as learning going on. After dozens of attempts, the UAV knows which action to take and seldom collides with the obstacles. Supposing that, if the UAV is able to fly in the environment without collisions for more than 1000 steps, we suggest that the training is done and the UAV has the ability to wander in an environment. Fig. 18 is the experiment of 21 trails. It shows attempt accounts before the success of trainings and the average attempt accounts (41 times). This means that, in most of the cases, the uav will finish its learning within 50 collisions. VI. Conclusion This paper presents a basal ganglia network centric computational model for autonomous learning (more specifically reinforcement learning). Compared to other related work, our model includes more cognitive evidence and biological details. For example, the Orbitofrontal Cortex (OFC) is considered as a learning control brain area. The Hodgkin-Huxley (H-H) model is used in our model to perform information coding process. In order to store accurate values in the memory, we propose a precise encoding method to send Cogn Comput 14 important values in the learning process into the working memory. In the experiment validations, we apply our basal ganglia network based models on UAV learning in unknown 3D environment. The results given by simulations indicate good autonomous learning ability of the UAV. We suggest that the UAV trained in an environment could be able to perform free exploration in another unknown environment without re-training. That is because the environment modeling has the distances between the UAV and the obstacles as the main information for environment evaluation. These kinds of distances have general suitability in most kinds of environment. The training for the UAV can be once and for all. Although from the application perspective, the UAV has a “built-in brain” and has good performance on autonomous learning based free exploration, there are several future work that could be done for improvement. Firstly, the Premotor Cortex (PMC) is associated with action selection [4, 8] and should be included in the next version of our model. Secondly, action space for the UAV is currently simple and the UAV’s posture angles are not fully considered (just the yaw angle, indicating turning degrees in horizontal plane) in the experiments. Including more posture angles will make the UAV more flexible but more hard to control. [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] COMPLIANCE WITH ETHICAL STANDARDS Funding: This study was funded by the Strategic Priority Research Program of the Chinese Academy of Sciences, and Beijing Municipal Science and Technology Commission. Ethical approval: This article does not contain any studies with human participants performed by any of the authors. [20] [21] [22] [23] REFERENCES [24] [1] [2] [3] [4] [5] [6] [7] [8] Stewart TC, Bekolay, Eliasmith C. Learning to select actions with spiking neurons in the basal ganglia. Frontiers in Neuroscience. 2012 Jan; 6(2): 1-14. Bekolay T, Eliasmith C. A general error-modulated STDP learning rule applied to reinforcement learning in the basal ganglia. Computational and Systems Neuroscience conference. 2011 Feb 24-27; Salt Lake City, Utah. Eliasmith C, Stewart TC, Choo X, Bekolay T, DeWolf T, Tang Y, et al. A large-scale model of the functioning brain. Science. 2012 Dec; 338(6111): 1202-5. Eliasmith C. How to build a brain. Reprint edition. New York: Oxford; 2013: 121-171. Chakravarthy VS, Joseph D, Bapi RS. What do the basal ganglia do? A modeling perspective. Biological Cybernetics. 2010 Sep; 103(3): 237-253. Stocco A, Lebiere C, Anderson JR. Conditional Routing of Information to the Cortex: A Model of the Basal Ganglia’s Role in Cognitive Coordination. Psychological Review. 2010 Apr; 117(2): 541–574. Maass W. Networks of spiking neurons: the third generation of neural network models. Neural Networks. 1997 Dec; 10(9): 1659-1671. Frank MJ. Dynamic dopamine modulation in the Basal Ganglia: a neuro computational account of cognitive deficits in medicated and nonmedicated parkinsonism. Journal of Cognitive Neuroscience. 2005 [25] [26] [27] [28] [29] [30] [31] [32] [33] Jan; 17(1): 51-72. Utter AA, Basso MA. The basal ganglia: an overview of circuits and function. Neuroscience & Biobehavioral Reviews. 2008 Jan; 32(3): 333-342. Redgrave P, Rodriguez M, Smith Y, Rodriguez-Oroz MC, Lehericy S, Bergman H, et al. Goal-directed and habitual control in the basal ganglia: implications for Parkinson’s disease. Nature Reviews Neuroscience. 2010 Nov; 11: 760-772. Stewart TC, Choo X, Eliasmith C. Dynamic behavior of a spiking model of action selection in the basal ganglia, Proceedings of the 10th International Conference on Cognitive Modeling. 2010 Aug 5-8; Philadelphia, PA. Frank MJ. Hold your horses: a dynamic computational role for the subthalamic nucleus in decision making. Neural Networks. 2006 Qct; 19(8): 1120-1136. Gurney K, Prescott TJ, Redgrave P. A computational model of action selection in the basal ganglia. Biological Cybernetics. 2001 Jun; 84(6): 401-410. Stewart TC, Eliasmith C. Large-scale synthesis of functional spiking neural circuits. Proceedings of IEEE. 2014 May; 102(5): 881-898. Frith C, Dolan R. The role of the prefrontal cortex in higher cognitive functions. Cognitive Brain Research. 1996 Dec; 5(1): 175-181. MacNeil D, Eliasmith C. Fine-tuning and the stability of recurrent neural networks. Public Library of Science (PLoS One). 2011 Sep; 6(9): 1-16. Gurney K, Prescott TJ, Wickens JR, Redgrave P. Computational models of the basal ganglia: from robots to membranes. Trends in Neuroscience. 2004 Aug; 27(8): 453-459. Albin RL, Young AB, Penney JB. The functional anatomy of basal ganglia disorders. Trends in Neuroscience. 1989 Qct; 12(10): 366-375. Bar-Gad I, Bergman H. Stepping out of the box: information processing in the neural networks of the basal ganglia. Current Opinion in Neurobiology. 2001 Dec; 11(6): 689-695. Iqarashi J, Shouno O, Fukai T, Tsujino H. Real-time simulation of a spiking neural network model of the basal ganglia circuitry using general purpose computing on graphics processing units. Neural Networks. 2011 Nov; 24(9): 950-960. Kringelbach ML. The human orbitofrontal cortex: linking reward to hedonic experience. Nature Reviews Neuroscience. 2005 Sep; 6(9): 691-702. Frank MJ, Claus ED. Anatomy of a decision: striato-orbitofrontal interactions in reinforcement learning, decision making, and reversal. Psychological Review. 2006 Apr; 113(2): 300-326. Cessac B, Paugam-Moisy H, Viéville T. Overview of facts and issues about neural coding by spikes. Journal of Physiology-Paris. Nov; 104(1): 5-18. Eliasmith C, Anderson CH. Neural Engineering. Computation Representation, and Dynamics in Neurobiological Systems. Cambridge, Massachusetts London, England: The MIT Press; 2003. Dethier J, Gilja V, Nuyujukian P, Elassaad SA, Shenoy KV. Spiking neural network decoder for brain-machine interfaces. IEEE conference on Neural Engineering. 2011 Apr 27-May 1; Cancun. Dayan P, Abbott LF. Computational and mathematical modeling of neural systems: Model Neurons I: Neuroelectronic. Cambridge: MIT Press; 2003. Izhikevich EM. Dynamical systems in neuroscience: the geometry of excitability and bursting. Cambridge, MA: MIT Press; 2004 Dec. Wang J, Chen LQ, Fei XY. Analysis and control of the bifurcation of Hodgkin-Huxley model. chaos, solitons and Fractals. 2007 Jan; 31(1): 247-256. Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology. 1952 Aug; 117(4): 500-544. Nelson ME. Electrophysiological Models In: databasing the brain: from Data to Knowledge. Wiley, New York; 2004. Gerstner W and Kistler WM. Spiking neuron models. Single Neurons, Populations, Plasticity. Cambridge: Cambridge University Press; 2002. Wells RB. Introduction to Biological signal processing and computational Neuroscience. Moscow, ID, USA; 2010. Long LN, Fang GL. A review of biologically plausible neuron models for Cogn Comput 15 [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] spiking neural networks. AIAA InfoTech Aerospace Conference. 2010 Apr. 20-22; Atlanta, GA. Weber C, Elshaw M, Wermter S, Triesch J, Willmot C. Reinforcement Learning: Theory and Applications: Reinforcement learning embedded in brains and robots. Vienna, Austria; 2008 Jan. Chee KY, Zhong ZW. Control, navigation and collision avoidance for an unmanned aerial vehicle. Sensors and Actuators. 2013 Feb; 190: 66-76. Kusterer R. jMonkeyEngine 3.0: Beginner’s Guide [Internet]. 2013 June [cited 2015 June 29]; Available from: https://www.packtpub.com/sites/default/files/9781849516464_Chapter _02_0.pdf. Vásárhelyi G, Virágh C, Somorjai G, Tarcai N, Szörényi T, Nepusz T, et al. Outdoor flocking and formation flight with autonomous aerial robots. IEEE Conference on Intelligent Robots and Systems. 2014 Sep. 14-18; Chicago, IL, USA. Szepesv´ari C. Algorithms for reinforcement learning. 1 ed. Morgan and Claypool; 2010. Ito M, Doya K. Multiple representations and algorithms for reinforcement learning in the cortico-basal ganglia circuit. Current Opinion in Neurobiology. 2011 June; 21(3): 368-373. Maia TV. Reinforcement learning, conditioning, and the brain: Successes and challenges. Cognitive, Affective, & Behavioral Neuroscience. 2009 Dec; 9(4): 343-364. Prescott TJ, Montes González FM, Gurney K, Humphries MD, Redgrave P. A robot model of the basal ganglia: behavior and intrinsic processing. Neural Networks. 2006 Jan; 19(1): 31-61. Takahashi YK1, Roesch MR, Stalnaker TA, Haney RZ, Calu DJ, Taylor AR, et al. The orbitofrontal cortex and ventral tegmental area are necessary for learning from unexpected outcomes. Neuron. 2009 Apr; 62(2): 269-280. Yang S, Yu Y, Zhou Z, Ying JH, Liu WX, Wang MX. HKUST IARC Team Progress Report [Internet]. International Aerial Robotics Competition. 2014 [cited 2015 Jun 30]; Available from: http://www.aerialroboticscompetition.org/2014SymposiumPapers/Hon gKongUniversityofScienceandTechnology.pdf. IARC. Official Rules for the International Aerial Robotics Competition [Internet]. International Aerial Robotics Competition. 2015 [cited 2015 June 30]; Available from: http://www.aerialroboticscompetition.org/rules.php.