querying description logic knowledge bases
... its instances, e.g., the concept EU can be defined as an enumeration of its member countries. Different DLs may have different computational properties. The time needed ...
... its instances, e.g., the concept EU can be defined as an enumeration of its member countries. Different DLs may have different computational properties. The time needed ...
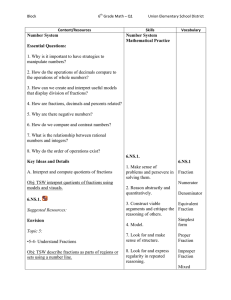
Number and Operations – Fractions
... 3. Miguel is making an obstacle course for field day. At the end of every sixth of the course, there is a tire. At the end of every third of the course, there is a cone. At the end of every half of the course, there is a hurdle. At which locations of the course will people need to go through more th ...
... 3. Miguel is making an obstacle course for field day. At the end of every sixth of the course, there is a tire. At the end of every third of the course, there is a cone. At the end of every half of the course, there is a hurdle. At which locations of the course will people need to go through more th ...
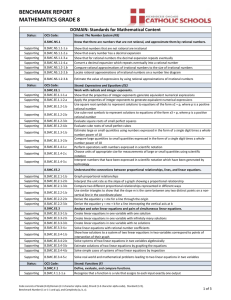
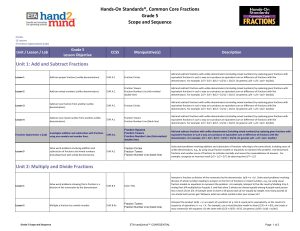
Common Core State Standards (CCSS) for Mathematics
... To perform this task, the staff of the Southeast Comprehensive Center (SECC) recognized the following situations: ...
... To perform this task, the staff of the Southeast Comprehensive Center (SECC) recognized the following situations: ...
g1020_ww9_aap
... The transmission of speech and other voiceband applications over packet networks brings with it new, sometimes unique forms of quality degradation. There are many existing definitions for packet network performance parameters, yet the desire to control the quality of non-elastic isochronous applicat ...
... The transmission of speech and other voiceband applications over packet networks brings with it new, sometimes unique forms of quality degradation. There are many existing definitions for packet network performance parameters, yet the desire to control the quality of non-elastic isochronous applicat ...
Document
... LEMMA: For all n, fn < 2n Proof. Base cases (both needed as can’t apply induction step on f1 since f-1 is undefined) n = 0: f0 = 0 < 1 = 20 n = 1: f1 = 1 < 2 = 21 Induction n > 0: fn = fn-1+fn-2 < 2n-1 + 2n-2 applying both P (n-1) and P (n-2) which can be assumed by strong induction hypothesis. ...
... LEMMA: For all n, fn < 2n Proof. Base cases (both needed as can’t apply induction step on f1 since f-1 is undefined) n = 0: f0 = 0 < 1 = 20 n = 1: f1 = 1 < 2 = 21 Induction n > 0: fn = fn-1+fn-2 < 2n-1 + 2n-2 applying both P (n-1) and P (n-2) which can be assumed by strong induction hypothesis. ...
Does machine learning need fuzzy logic?
... Without denying the potential usefulness of fuzzy logic in constructing interpretable models in general, the author is quite convinced that current fuzzy machine learning methods produce models that are not at all more interpretable than any other types of model, and often even less. There are sever ...
... Without denying the potential usefulness of fuzzy logic in constructing interpretable models in general, the author is quite convinced that current fuzzy machine learning methods produce models that are not at all more interpretable than any other types of model, and often even less. There are sever ...