Download mathematical induction

Kontraktbaseret Programmering 1
Induction and Recursion
Jens Bennedsen
Agenda
 Syllabus for this week
• Recursive definitions of sets
• Recursive definitions of algorithms
• Mathematical Induction – First Principle
• Mathematical Induction – Second Principle
Slide 2
Ingeniørhøjskolen i Århus
Syllabus for this week
• Discrete Structures Web Course Material
– Section 5A: Recursive Definitions
– Section 5D: Proof by Induction
– But these web pages also contain material about
•
•
•
•
•
Propositional logic
Predicate logic
Sets
Relations and
Functions
– Including on-line interactive exercises
– May be handy for repetition before exam
Slide 3
Ingeniørhøjskolen i Århus
Agenda
 Syllabus for this week
 Recursive definitions of sets
• Recursive definitions of algorithms
• Mathematical Induction – First Principle
• Mathematical Induction – Second Principle
Slide 4
Ingeniørhøjskolen i Århus
Recursive Definition of a set
• The basis clause:
– What are the basic starting elements of the set.
• The inductive clause:
– In which ways can existing elements be combined to
produce new elements.
• The extremal clause:
– Unless an object can be shown to be a member of the
set by applying the first two clauses it is not a member
of the set.
Slide 5
Ingeniørhøjskolen i Århus
Example: The natural numbers
• The set of the natural numbers can be defined as:
– Basis clause: 0  N.
– Inductive clause: For any element x in N, x + 1 is in N.
– Extremal clause: Nothing is in N unless it is obtained
from either the basis or the inductive clauses.
• The “x + 1” is also called “succ(x)” in the literature
• This was formalized by the mathematician Peano
Slide 6
Ingeniørhøjskolen i Århus
How to define the even natural numbers?
• The set of the even natural numbers (NE) can be
defined as:
– Basis clause: 0  NE.
– Inductive clause: For any element x in NE, x + 2 is in
NE.
– Extremal clause: Nothing is in NE unless it is obtained
from either the basis or the inductive clauses.
Slide 7
Ingeniørhøjskolen i Århus
How to define the even integers?
• The set of the even integers (EI) can be defined
as:
– Basis clause: 0  EI.
– Inductive clause: For any element x in EI, x + 2 and x -2
are in EI.
– Extremal clause: Nothing is in EI unless it is obtained
from either the basis or the inductive clauses.
Slide 8
Ingeniørhøjskolen i Århus
How to define propositional forms?
• Let V = {p,q,r,…} be a set of propositional
variables, where V does not contain any of the
following symbols: (, ), , , , , , T and F.
Then the set of the propositional forms can be
defined as:
– Basis clause: T and F are propositional forms and if x V
then x is a propositional form.
– Inductive clause: If E1 and E2 are propositional forms
then (E1), (E1  E2), (E1  E2), (E1  E2), (E1  E2)
are all propositional forms.
– Extremal clause: Nothing is a propositional form unless it
is obtained from either the basis or the inductive clauses.
Slide 9
Ingeniørhøjskolen i Århus
Agenda
 Syllabus for this week
 Recursive definitions of sets
 Recursive definitions of algorithms
• Mathematical Induction – First Principle
• Mathematical Induction – Second Principle
Slide 10
Ingeniørhøjskolen i Århus
Recursive Thinking
• Recursion is a problem-solving approach that can
be used to generate simple solutions to certain
kinds of problems that would be difficult to solve in
other ways
• Recursion splits a problem into one or more
simpler versions of itself
Slide 11
Ingeniørhøjskolen i Århus
Recursion in practice
Slide 12
Ingeniørhøjskolen i Århus
Recursion Recipe
1. Handle the “base case”, where a recursive call is not
made.
2. For the other cases, make a recursive call (the recursive
“leap of faith”), which must make progress towards a
goal (towards the base case)
3. Typically no need for an extremal clause
If the base case is not handled,
or the recursive call does not progress towards the base case,
then the method will call itself infinitely
(it will “diverge”).
Slide 13
Ingeniørhøjskolen i Århus
Recursive Definitions of Algorithms
• The factorial N!, for any positive integer N, is
defined to be the product of all integers between 1
and N inclusive
• This definition can be expressed recursively as:
1!
N!
=
=
1
N * (N-1)!
• A factorial is defined in terms of another factorial
• Eventually, the base case of 1! is reached
Slide 14
Ingeniørhøjskolen i Århus
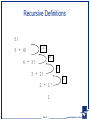
Recursive Definitions
5!
120
5 * 4!
24
4 * 3!
6
3 * 2!
2
2 * 1!
1
Slide 15
Ingeniørhøjskolen i Århus
A recursive C++ algorithm for factorial
// Precondition n >= 1
// Postcondition result is n!
int recursiveFac(int n)
Base case
{
if(n==1) return 1;
else return n*recursiveFac(n-1);
}
Recursive case
Slide 16
Ingeniørhøjskolen i Århus
Fibonacci numbers
• Developed by Leonardo Pisano in 1202.
– Investigating how fast rabbits could breed under
idealized circumstances.
– Assumptions
• A pair of male and female rabbits always breed and produce
another pair of male and female rabbits.
• A rabbit becomes sexually mature after one month, and that the
gestation period is also one month.
– Pisano wanted to know the answer to the question how
many rabbits would there be after one year?
Slide 17
Ingeniørhøjskolen i Århus
Fibonacci Numbers
• The Fibonacci Numbers are defined by
– The first two numbers are 1 and 1.
– Each subsequent number is the sum of the preceding 2
numbers.
• 1,1,2,3,5,8,13,21,34,55,etc.
• Recursively it is defined as:
•
•
•
•
Fibonachi(n) = 1
if n = 0
Fibonachi(n) = 1
if n = 1
Fibonachi(n) = Fibonachi(n-2) + Fibonachi(n-1) otherwise
Non-recursively:
n
n
1 5  1 5
F ( n) 
5  2n

 
Slide 18

Ingeniørhøjskolen i Århus
The fibonacci Method
// Precondition: n >= 0
// Postcondition: The corresponding fibonachi number is
//
returned
long fibonacci(long n){
int fib;
if (n <= 1)
return 1;
Base case
else
return fibonacci(n-1) + fibonacci(n-2);
}
Recursive case
Slide 19
Ingeniørhøjskolen i Århus
Execution Trace (decomposition)
fibonacci(3)
fibonacci(1)
fibonacci(2)
Slide 20
Ingeniørhøjskolen i Århus
Execution Trace (decomposition)
fibonacci(3)
fibonacci(1)
fibonacci(2)
fibonacci(1)
fibonacci(0)
Slide 21
Ingeniørhøjskolen i Århus
Execution Trace (composition)
fibonacci(3)
+
fibonacci(1)
fibonacci(2)
+
fibonacci(1)->1
fibonacci(0)->1
Slide 22
Ingeniørhøjskolen i Århus
Execution Trace (composition)
fibonacci(3)
+
fibonacci(2)->2
Slide 23
fibonacci(1)->1
Ingeniørhøjskolen i Århus
Execution Trace (composition)
fibonacci(3)->3
Slide 24
Ingeniørhøjskolen i Århus
Towers of Hanoi
In the great temple of Brahma in Benares, on a brass
plate under the dome that marks the center of the world,
there are 64 disks of pure gold that the priests carry one at a
time between these diamond needles according to Brahma's
immutable law: No disk may be placed on a smaller disk. In
the beginning of the world all 64 disks formed the Tower of
Brahma on one needle. Now, however, the process of
transfer of the tower from one needle to another is in mid
course. When the last disk is finally in place, once again
forming the Tower of Brahma but on a different needle, then
will come the end of the world and all will turn to dust.
R. Douglas Hofstadter. Metamagical themas. Scientific American,
248(2):16-22, March 1983.
Slide 25
Ingeniørhøjskolen i Århus
Towers of Hanoi Problem with Three Disks
Slide 26
Ingeniørhøjskolen i Århus
Towers of Hanoi: Three Disk Solution
Slide 27
Ingeniørhøjskolen i Århus
Towers of Hanoi: Three Disk Solution
Slide 28
Ingeniørhøjskolen i Århus
Towers of Hanoi: Recursive Function
The general algorithm to solve this problem is
1. Move the top n-1 disks from needle 1 to
needle 2 using needle 3 as the
intermediate needle
2. Move disk number n from needle 1 to
needle 3
3. Move the top n-1 disks from needle 2 to
needle 3 using needle 1 as the
intermediate needle
Slide 29
Ingeniørhøjskolen i Århus
Recursive Towers of Hanoi in C++
// Precondition: count >= 0
// Postcondition: count disks are moved from from_needle
//
to to_needle using via_needle for help
void moveDisks(int count, int from_needle, int to_needle,
int via_needle)
{
if(count > 0)
Recursive call
{
moveDisks(count - 1, from_needle, via_needle, to_needle);
cout<<"Move disk "<<count<<“ from "<<from_needle
<<“ to "<<to_needle<<"."<<endl;
moveDisks(count - 1, via_needle, to_needle, from_needle);
}
}
Recursive call
Slide 30
Ingeniørhøjskolen i Århus
General problem solving strategy
• Divide and conquer
solve(p: Problem) {
if <p is a simple problem>
solution = <solve it directly>
else
<split p in two disjoint problems p1 and p2>
res1 = solve(p1)
res2 = solve(p2)
solution = join(p1, p2)
Slide 31
Ingeniørhøjskolen i Århus
Example: search
private bool search(int m, List<int> p)
{
if (p.Count == 0)
return false;
else if (p.Count == 1)
return p[0] == m;
else
{
List<int> p1 = new List<int>();
List<int> p2 = new List<int>();
for (int i = 0; i < p.Count / 2; i++)
p1[i] = p[i];
for (int j = (p.Count / 2) + 1; j < p.Count; j++)
p2[j - ((p.Count / 2) + 1)] = p[j];
return search(m, p1) || search(m, p2);
}
}
Slide 32
Ingeniørhøjskolen i Århus
Agenda
 Syllabus for this week
 Recursive definitions of sets
 Recursive definitions of algorithms
 Mathematical Induction – First Principle
• Mathematical Induction – Second Principle
Slide 33
Ingeniørhøjskolen i Århus
Mathematical Induction
• In the mathematical induction we have the law
already formulated. We must prove that it holds
generally
• The basis for mathematical induction is the
property of the well-ordering principle for the
natural numbers
Slide 34
Ingeniørhøjskolen i Århus
1. principle of Mathematical Induction
•
•
•
Also called weak induction
Suppose P(n) is a statement involving an integer n
Then to prove that P(n) is true for every n ≥ n0 it is
sufficient to show that these two things hold:
1. P(n0) is true
2. For any k ≥ n0, if P(k) is true, then P(k+1) is true
– In general we have a basis step
– Followed by an inductive step.
Slide 35
Ingeniørhøjskolen i Århus
Example Induction Proof
• Prove that for any natural number n it holds that:
0+1+…+n = n(n + 1)/2
– Basis step: If n = 0 then LHS = 0 and RHS = 0(0+1)/2=0
– Induction step: Let the induction hypothesis be:
For an arbitrary k it holds that 0+1+…+k = k(k + 1)/2
Let us try to express LHS for (k+1). Using the induction
hypothesis the LHS = k(k+1)/2 + (k+1)
If we factor out (k+1) we can rewrite this to: (k+1)(k+2)/2
This is identical to the RHS for (k+1)
QED.
Slide 36
Ingeniørhøjskolen i Århus
Example Induction Proof
• Prove that for any natural number n it holds that:
1+3+…+(2n+1) = (n + 1)2
– Check for n = 0: 2*0 + 1 = (0 + 1)2
– Assume that:
For an arbitrary k it holds that 1+3+…+(2k+1) = (k + 1)2
Then for k+1 we need to prove:
1+3+…+(2k+1)+(2(k+1)+1) = ((k+1)+1)2
Using the induction hypothesis we get:
1+3+…+(2k+1)+(2(k+1)+1) = (k+1)2 + (2(k+1) +1)
Since (k+1)2 + 2(k+1)+1 = (k+1+1)2 we have proved our
objective.
QED.
Slide 37
Ingeniørhøjskolen i Århus
More on Inductive Proofs
General strategy:
Clarify on which variable you are going to do the
induction
Calculate some small cases n=0,1,2,3,…
(Come up with your conjecture)
Make clear what the induction step nn+1 is
Prove it, and say that you proved it.
Slide 38
Ingeniørhøjskolen i Århus
Agenda
 Syllabus for this week
 Recursive definitions of sets
 Recursive definitions of algorithms
 Mathematical Induction – First Principle
 Mathematical Induction – Second Principle
Slide 39
Ingeniørhøjskolen i Århus
2. principle of Mathematical Induction
•
•
•
Also called strong induction
Suppose P(n) is a statement involving an integer n
Then to prove that P(n) is true for every n ≥ n0 it is
sufficient to show that this holds:
1. P(n0) is true
2. For any k ≥ n0, if P(x) is true for all x smaller than k, then
P(k) is true
Slide 40
Ingeniørhøjskolen i Århus
Strong induction
• Weak mathematical induction assumes P(k) is
true, and uses that (and only that!) to show P(k+1)
is true
• Strong mathematical induction assumes P(1),
P(2), …, P(k) are all true, and uses that to show
that P(k+1) is true.
P(1)  P(2)  P(3)  ...  P(k )  P(k 1)
Slide 41
Ingeniørhøjskolen i Århus
Strong induction example
• Show that any number > 1 can be written as the
product of primes
• Base case: P(2)
– 2 is the product of 2 (remember that 1 is not prime!)
• Inductive hypothesis: P(1), P(2), P(3), …, P(k) are
all true
• Inductive step: Show that P(k+1) is true
Slide 42
Ingeniørhøjskolen i Århus
Strong induction example
• Inductive step: Show that P(k+1) is true
• There are two cases:
– k+1 is prime
• It can then be written as the product of k+1
– k+1 is composite
• It can be written as the product of two composites, a and b,
where 2 ≤ a ≤ b < k+1
• By the inductive hypothesis, both P(a) and P(b) are true
– QED

Slide 43
Ingeniørhøjskolen i Århus
Induction in Computer Science
Inductive proofs play an important role in computer
science because of their similarity with recursive
algorithms.
Analyzing recursive algorithms often require the
use of recurrent equations, which require inductive
proofs.
Also, recursive algorithms are constructive such
that we often get a solution “for free”.
Slide 44
Ingeniørhøjskolen i Århus
Summary
• The notion of Recursion and Induction
– Recursive definitions of sets
– Recursive definitions of algorithms
– Mathematical Induction
• Read Section 5A: Recursive Definitions and
Section 5D: Proof by Induction from the web
pages on slide 3
• Carry out as many exercises as possible from the
web pages
Slide 45
Ingeniørhøjskolen i Århus