Math
... horse and rider. The horse stepped on her basket and crushed the eggs in her basket. The rider offered to pay for the broken eggs and asked how many eggs were in the basket. She did not remember the exact number, but when she had taken them out two at a time, there was one egg left. The same happene ...
... horse and rider. The horse stepped on her basket and crushed the eggs in her basket. The rider offered to pay for the broken eggs and asked how many eggs were in the basket. She did not remember the exact number, but when she had taken them out two at a time, there was one egg left. The same happene ...
List of available projects - HTTrack Website Copier
... Step. 16 : Divide 8 by 2 i.e.,, 0.0526315789473684 ( 4 times, No remainder ) Step. 17 : Divide 4 by 2 i.e.,, 0.05263157894736842 ( 2 times, No remainder ) Step. 18 : Divide 2 by 2 i.e.,, 0.052631578947368421 ( 1 time, No remainder ) Now from step 19, i.e.,, dividing 1 by 2, Step 2 to Step. 18 repeat ...
... Step. 16 : Divide 8 by 2 i.e.,, 0.0526315789473684 ( 4 times, No remainder ) Step. 17 : Divide 4 by 2 i.e.,, 0.05263157894736842 ( 2 times, No remainder ) Step. 18 : Divide 2 by 2 i.e.,, 0.052631578947368421 ( 1 time, No remainder ) Now from step 19, i.e.,, dividing 1 by 2, Step 2 to Step. 18 repeat ...
GRADE 8 STAAR Format Mini-Assessments And Periodic
... Results can and should be recorded in the Class Profile to reflect the entire class performance and on the Student Profile for the student’s performance. An answer key is provided for the Mini-Assessments and Periodic Assessments. Teachers should consider creating a personal Solution Manual to bec ...
... Results can and should be recorded in the Class Profile to reflect the entire class performance and on the Student Profile for the student’s performance. An answer key is provided for the Mini-Assessments and Periodic Assessments. Teachers should consider creating a personal Solution Manual to bec ...
5-CON TRIANGLES - Antonella Perucca
... Two triangles are said to be 5-Con or almost congruent if they are not congruent triangles but they are similar triangles and share two side lengths (of non-corresponding sides). The 5-Con triangles are important examples for understanding the solution of triangles. Indeed, knowing three angles and ...
... Two triangles are said to be 5-Con or almost congruent if they are not congruent triangles but they are similar triangles and share two side lengths (of non-corresponding sides). The 5-Con triangles are important examples for understanding the solution of triangles. Indeed, knowing three angles and ...
mathematics 2º eso - IES Andrés de Vandelvira
... 1. Count the number of negative numbers in the product. 2. Take the product of their absolute values. If the number of negative integers counted in step 1 is even, the product is just the product from step 2 (positive). If the number of negative integers is odd, the product is the opposite of the pr ...
... 1. Count the number of negative numbers in the product. 2. Take the product of their absolute values. If the number of negative integers counted in step 1 is even, the product is just the product from step 2 (positive). If the number of negative integers is odd, the product is the opposite of the pr ...
Grade 6 Alternate Eligible Math Content
... Example 2: “We paid $75 for 15 hamburgers, which is a rate of $5 per hamburger.” M06.A-R.1.1.3 Construct tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and/or plot the pairs of values on the coordinate plane. Use tables to compare r ...
... Example 2: “We paid $75 for 15 hamburgers, which is a rate of $5 per hamburger.” M06.A-R.1.1.3 Construct tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and/or plot the pairs of values on the coordinate plane. Use tables to compare r ...
Common Core State Standards (CCSS) for Mathematics
... groups, area models, and equal-sized moves on the number line. (DOK 2) ...
... groups, area models, and equal-sized moves on the number line. (DOK 2) ...
Document
... Induction n > 1: Consider n horses. Removing last horse we have a group of n-1 horses. By induction, me may assume P (n-1) true, so the first n -1 horses are color consistent. By a similar argument, the last n-1 horses are consistent also. But since the first n-1 horses and last n-1 horses are consi ...
... Induction n > 1: Consider n horses. Removing last horse we have a group of n-1 horses. By induction, me may assume P (n-1) true, so the first n -1 horses are color consistent. By a similar argument, the last n-1 horses are consistent also. But since the first n-1 horses and last n-1 horses are consi ...
Chapter 6
... else if (key > a[mid]) /* recursive call */ return binsearch (a, mid + 1, high, key); else /* if (key == a[mid]) */ return mid; ...
... else if (key > a[mid]) /* recursive call */ return binsearch (a, mid + 1, high, key); else /* if (key == a[mid]) */ return mid; ...
Mathematical Olympiad in China : Problems and Solutions
... The first time China sent a team to IMO was in 1985. At that time, two students were sent to take part in the 26th IMO. Since 1986, China has always sent a team of 6 students to IMO except in 1998 when it was held in %wan. So far (up to 2006) , China has achieved the number one ranking in team effor ...
... The first time China sent a team to IMO was in 1985. At that time, two students were sent to take part in the 26th IMO. Since 1986, China has always sent a team of 6 students to IMO except in 1998 when it was held in %wan. So far (up to 2006) , China has achieved the number one ranking in team effor ...
picture_as_pdf Mathematics Grades 10–12
... individual interests, abilities, needs and career goals. They come to school with varying knowledge, life experiences, expectations and backgrounds. A key component in developing mathematical literacy in students is making connections to these backgrounds, experiences, goals and aspirations. Student ...
... individual interests, abilities, needs and career goals. They come to school with varying knowledge, life experiences, expectations and backgrounds. A key component in developing mathematical literacy in students is making connections to these backgrounds, experiences, goals and aspirations. Student ...
historical notes - Indian National Science Academy
... his mathematical work, has come under his wondrous spell. One cannot think about ‘Ramanujan’s life without some appreciation of Mathematics that he lived for and loved’. Profundity and richness in his works has been manifest even at the elementary level of mathematics. Here is a humble attempt to na ...
... his mathematical work, has come under his wondrous spell. One cannot think about ‘Ramanujan’s life without some appreciation of Mathematics that he lived for and loved’. Profundity and richness in his works has been manifest even at the elementary level of mathematics. Here is a humble attempt to na ...
Number systems - The Open University
... can be represented as points in the plane and state the Fundamental Theorem of Algebra: that any polynomial equation with complex coefficients has a solution which is a complex number. We will also define the function exp of a complex variable. Earlier we mentioned several sets of numbers, including ...
... can be represented as points in the plane and state the Fundamental Theorem of Algebra: that any polynomial equation with complex coefficients has a solution which is a complex number. We will also define the function exp of a complex variable. Earlier we mentioned several sets of numbers, including ...
Introduction to Writing Proofs in Mathematics
... must be able to discover and construct proofs. In addition, once the discovery has been made, the mathematician must be able to communicate this discovery to others who speak the language of mathematics. We will be dealing with these ideas throughout the text. For now, we want to focus on what happe ...
... must be able to discover and construct proofs. In addition, once the discovery has been made, the mathematician must be able to communicate this discovery to others who speak the language of mathematics. We will be dealing with these ideas throughout the text. For now, we want to focus on what happe ...
- ScholarWorks@GVSU
... must be able to discover and construct proofs. In addition, once the discovery has been made, the mathematician must be able to communicate this discovery to others who speak the language of mathematics. We will be dealing with these ideas throughout the text. For now, we want to focus on what happe ...
... must be able to discover and construct proofs. In addition, once the discovery has been made, the mathematician must be able to communicate this discovery to others who speak the language of mathematics. We will be dealing with these ideas throughout the text. For now, we want to focus on what happe ...
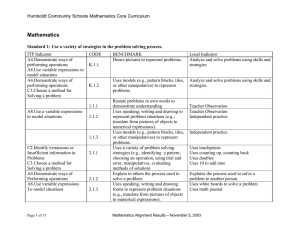
Math - Humboldt Community School District
... Using logical reasoning arguments Predict or estimate Justify answers in verbal and written form Understand that some ways of State problems in own works to increase representing a problem are more understanding helpful than others. Distinguish between pertinent and irrelevant ...
... Using logical reasoning arguments Predict or estimate Justify answers in verbal and written form Understand that some ways of State problems in own works to increase representing a problem are more understanding helpful than others. Distinguish between pertinent and irrelevant ...
4Fractions - IES Andrés de Vandelvira
... 1. To compare fractions with the same denominator, look at their numerators. The largest fraction is the one with the largest numerator. 2. To compare fractions with different denominators, take the cross product. Compare the cross products. a. If the cross-products are equal, the fractions are equi ...
... 1. To compare fractions with the same denominator, look at their numerators. The largest fraction is the one with the largest numerator. 2. To compare fractions with different denominators, take the cross product. Compare the cross products. a. If the cross-products are equal, the fractions are equi ...
mathematical induction
... • In the mathematical induction we have the law already formulated. We must prove that it holds generally • The basis for mathematical induction is the property of the well-ordering principle for the natural numbers ...
... • In the mathematical induction we have the law already formulated. We must prove that it holds generally • The basis for mathematical induction is the property of the well-ordering principle for the natural numbers ...
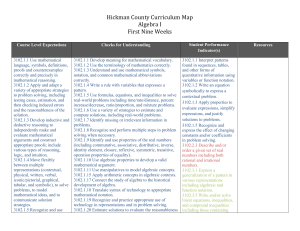
Algebra I - Hickman County Schools
... 3102.2.2 Apply the order of operations to simplify and evaluate algebraic expressions. 3102.2.7 Identify the subsets in the real number system and understand their relationships. 3102.2.8 Use multiple strategies to approximate the value of an irrational number including irrational square roots and i ...
... 3102.2.2 Apply the order of operations to simplify and evaluate algebraic expressions. 3102.2.7 Identify the subsets in the real number system and understand their relationships. 3102.2.8 Use multiple strategies to approximate the value of an irrational number including irrational square roots and i ...
History of Mathematics
... restraints. Richard Dedekind, for example, proved the existence of an infinite set by referring to the set of his possible thoughts. This set is infinite because, given any thought S0 , there is also the thought S1 that he is having thought S0 , the thought S2 that he is having thought S1 , etc. Dedek ...
... restraints. Richard Dedekind, for example, proved the existence of an infinite set by referring to the set of his possible thoughts. This set is infinite because, given any thought S0 , there is also the thought S1 that he is having thought S0 , the thought S2 that he is having thought S1 , etc. Dedek ...
Logic and discrete mathematics (HKGAB4) http://www.ida.liu.se
... {John, M ary, P aul, Eve} ∪ {P aul, Eve, Chris} = = {John, M ary, P aul, Eve, Chris} ...
... {John, M ary, P aul, Eve} ∪ {P aul, Eve, Chris} = = {John, M ary, P aul, Eve, Chris} ...
Fibonacci Identities as Binomial Sums
... Finding the exact value of Fn from (2) requires multiple steps of busy and messy algebraic calculations which is not desirable. So, our goal in this note is to present Fn as a binomial sum for quick numerical calculations. Likewise, we use this binomial sum to write some well-known and fundamental i ...
... Finding the exact value of Fn from (2) requires multiple steps of busy and messy algebraic calculations which is not desirable. So, our goal in this note is to present Fn as a binomial sum for quick numerical calculations. Likewise, we use this binomial sum to write some well-known and fundamental i ...
On Cantor`s diagonal argument
... mathematicians and philosophers such as Kronecker, Poincaré, Brouwer and Wittgenstein. As an Intuitionist, Brouwer said: “The … point of view that there are no non-experienced truths and that logic is not an absolutely reliable instrument to discover truths, has found acceptance with regard to mathe ...
... mathematicians and philosophers such as Kronecker, Poincaré, Brouwer and Wittgenstein. As an Intuitionist, Brouwer said: “The … point of view that there are no non-experienced truths and that logic is not an absolutely reliable instrument to discover truths, has found acceptance with regard to mathe ...
Running Time of Euclidean Algorithm
... Strong Induction Completing Example So now can complete stuck proof: LEMMA: For all n, fn < 2n Proof. Base cases (both needed as can’t apply induction step on f1 since f-1 is undefined) n = 0: f0 = 0 < 1 = 20 n = 1: f1 = 1 < 2 = 21 Induction n > 0: fn = fn-1+fn-2 < 2n-1 + 2n-2 applying both P ( ...
... Strong Induction Completing Example So now can complete stuck proof: LEMMA: For all n, fn < 2n Proof. Base cases (both needed as can’t apply induction step on f1 since f-1 is undefined) n = 0: f0 = 0 < 1 = 20 n = 1: f1 = 1 < 2 = 21 Induction n > 0: fn = fn-1+fn-2 < 2n-1 + 2n-2 applying both P ( ...