Elementary Problems and Solutions
... Edited by S.L. Basin To:Fibonacci and Lucas identities, 1.1(1963)76 So: Lucas Analogues, 2.1(1964)78 To:Fibonacci product and sum identities, 1.1(1963)76 So: Telescoping Products and Sums, 2.1(1964)78 So: Recursive Polynomial Sequences, 2.4(1964)325 To:Fibonacci matrix, 1.4(1963)73 So: Lambda Functi ...
... Edited by S.L. Basin To:Fibonacci and Lucas identities, 1.1(1963)76 So: Lucas Analogues, 2.1(1964)78 To:Fibonacci product and sum identities, 1.1(1963)76 So: Telescoping Products and Sums, 2.1(1964)78 So: Recursive Polynomial Sequences, 2.4(1964)325 To:Fibonacci matrix, 1.4(1963)73 So: Lambda Functi ...
TRAPEZOIDAL APPROXIMATION OF FUZZY NUMBERS
... most cases, it is considered a new Mathematics, very useful in solving problems expressed through a vague language. The promoter of the fuzzy sets theory, professor L. Zadeh, states that fuzzy Mathematics is a useful instrument in moulding problems which are either ungradable or too complex to be ad ...
... most cases, it is considered a new Mathematics, very useful in solving problems expressed through a vague language. The promoter of the fuzzy sets theory, professor L. Zadeh, states that fuzzy Mathematics is a useful instrument in moulding problems which are either ungradable or too complex to be ad ...
- Information Age Education
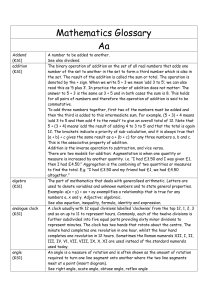
... no type number a natural number that is not a deficient number, abundant number, or perfect number. The one-and-only ‘no type’ number is 1. 1 has no proper factors. A deficient number is not a number with a personality defect. Deficient numbers can be very mathemagical. For example, ALL prime number ...
... no type number a natural number that is not a deficient number, abundant number, or perfect number. The one-and-only ‘no type’ number is 1. 1 has no proper factors. A deficient number is not a number with a personality defect. Deficient numbers can be very mathemagical. For example, ALL prime number ...
Student_Solution_Chap_09
... 1. A positive integer is a prime if and only if it is exactly divisible by two integers, 1 and itself. A composite is a positive integer with more than two divisors. ...
... 1. A positive integer is a prime if and only if it is exactly divisible by two integers, 1 and itself. A composite is a positive integer with more than two divisors. ...
Primetime
... a. If each rectangle is made with an even number of tiles that is greater than 40 but less than 60, how many tiles does it take to make each rectangle? Explain your reasoning. b. What is the length of each of Kyong’s rectangles? Explain your reasoning. c. Without changing the number of tiles used to ...
... a. If each rectangle is made with an even number of tiles that is greater than 40 but less than 60, how many tiles does it take to make each rectangle? Explain your reasoning. b. What is the length of each of Kyong’s rectangles? Explain your reasoning. c. Without changing the number of tiles used to ...