* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture7
Long non-coding RNA wikipedia , lookup
Short interspersed nuclear elements (SINEs) wikipedia , lookup
Expanded genetic code wikipedia , lookup
Public health genomics wikipedia , lookup
Ridge (biology) wikipedia , lookup
Biology and consumer behaviour wikipedia , lookup
Epigenetics of neurodegenerative diseases wikipedia , lookup
Vectors in gene therapy wikipedia , lookup
No-SCAR (Scarless Cas9 Assisted Recombineering) Genome Editing wikipedia , lookup
Primary transcript wikipedia , lookup
Transposable element wikipedia , lookup
History of genetic engineering wikipedia , lookup
Gene desert wikipedia , lookup
Genomic library wikipedia , lookup
Gene expression programming wikipedia , lookup
Gene nomenclature wikipedia , lookup
Genomic imprinting wikipedia , lookup
Nutriepigenomics wikipedia , lookup
Minimal genome wikipedia , lookup
Metagenomics wikipedia , lookup
Non-coding DNA wikipedia , lookup
Genome (book) wikipedia , lookup
Frameshift mutation wikipedia , lookup
Epigenetics of human development wikipedia , lookup
Human genome wikipedia , lookup
Pathogenomics wikipedia , lookup
Microevolution wikipedia , lookup
Gene expression profiling wikipedia , lookup
Point mutation wikipedia , lookup
Site-specific recombinase technology wikipedia , lookup
Designer baby wikipedia , lookup
Genome evolution wikipedia , lookup
Smith–Waterman algorithm wikipedia , lookup
Genome editing wikipedia , lookup
Genetic code wikipedia , lookup
Therapeutic gene modulation wikipedia , lookup
Dynamic Programming
(cont’d)
CS 466
Saurabh Sinha
Affine Gap Penalties
• In nature, a series of k indels often come as a single
event rather than a series of k single nucleotide
events:
ATA__GGC
ATGATCGC
This is more
likely.
ATA_G_GC
ATGATCGC
Normal scoring would
give the same score This is less
for both alignments
likely.
Accounting for Gaps
• Gaps- contiguous sequence of spaces in one of the rows
• Score for a gap of length x is:
-(ρ + σx)
where ρ >0 is the penalty for introducing a gap:
gap opening penalty
ρ will be large relative to σ:
gap extension penalty
because you do not want to add too much of a penalty for
extending the gap.
Affine gap penalty in DP
• When computing si,j, need to look at si,j-1,
si,j-2, si,j-3,…. and si-1,j, si-2,j, …
• Each cell needs O(n) time for update
• O(n2) cells
• Therefore, O(n3) algorithm
• We can still do this in O(n2) time
Affine Gap Penalty
Recurrences
si,j =
max
s i-1,j - σ
s i-1,j –(ρ+σ)
Continue Gap in w (deletion)
Start Gap in w (deletion): from middle
si,j =
max
s i,j-1 - σ
s i,j-1 –(ρ+σ)
Continue Gap in v (insertion)
si,j =
max
si-1,j-1 + δ (vi, wj) Match or Mismatch
End deletion: from top
s i,j
End insertion: from bottom
s i,j
Start Gap in v (insertion):from middle
Optional Reading
Section 6.10 (J & P)
Multiple Alignment
Gene Prediction
Gene Prediction: Computational Challenge
• Gene: A sequence of nucleotides coding
for protein
• Gene Prediction Problem: Determine the
beginning and end positions of genes in a
genome
SOURCE:
http://www.bioscience.org/atlases/genecode/genecode.htm
Codons
• In 1961 Sydney Brenner and Francis Crick
discovered frameshift mutations
• Systematically deleted nucleotides from
DNA
– Single and double deletions dramatically
altered protein product
– Effects of triple deletions were minor
– Conclusion: every triplet of nucleotides,
each codon, codes for exactly one
amino acid in a protein
Great Discovery Provoking Wrong Assumption
• In 1964, Charles Yanofsky and Sydney Brenner
proved colinearity in the order of codons with
respect to amino acids in proteins
• As a result, it was incorrectly assumed that the
triplets encoding for amino acid sequences form
contiguous strips of information.
Exons and Introns
• In eukaryotes, the gene is a combination of
coding segments (exons) that are interrupted by
non-coding segments (introns)
• This makes computational gene prediction in
eukaryotes even more difficult
• Prokaryotes don’t have introns - Genes in
prokaryotes are continuous
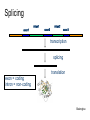
Splicing
exon1
intron1
exon2
intron2
exon3
transcription
splicing
exon = coding
intron = non-coding
translation
Batzoglou
Gene prediction
• More difficult in eukaryotes than in
prokaryotes (due to introns).
• In human genome, ~3% of DNA
sequence is genes
• Lot of “junk” DNA between genes, and
even inside genes (between exons).
• Gene prediction must deal with this.
Gene prediction: broadly
speaking
• Statistical approaches:
look for features than appear frequently in
genes and infrequently elsewhere
• Similarity based approaches: a newly
sequenced gene may be similar to a known
gene.
– even this is not so simple. The exon structures
may be different between otherwise similar genes
Statistical approaches
Open Reading Frames (ORFs)
• Let us consider gene prediction in prokaryotes (no introns)
• Detect potential coding regions by looking at ORFs
– A region of length n is comprised of (n/3) codons
– Stop codons break genome into segments between
consecutive Stop codons
– The subsegments of these that start from the Start codon
(ATG) are ORFs
ATG
TGA
Genomic Sequence
Open reading frame
ORFs
• 6 reading frames in any given sequence
– 6 ways to map the DNA sequence to codon
sequence (+1,+2,+3,-1,-2,-3)
– 3 on either strand
• Look at all 6 reading frames for ORFs
Long vs.Short ORFs
• Long open reading frames may be a gene
– At random, we should expect one stop codon
every (64/3) ~= 21 codons
– However, genes are usually much longer than
this
• A basic approach is to scan for ORFs whose length
exceeds certain threshold
– This is naïve because some genes (e.g. some
neural and immune system genes) are relatively
short
Codon usage
• In a given sequence (e.g., an ORF), compute
frequency distribution of codons (64 element array):
codon usage array
• Codon usage array for coding sequences is different
from that for non-coding sequences
• If the codon usage array for an ORF is much more
similar to that of coding sequences than to that of
non-coding sequences, the ORF could be a gene
Codon usage
• Codons coding for “Arg” in human:
– CGU: 37%, CGC: 38%, CGA: 7%, CGG:
10%, AGA: 5%, AGG: 3%
– In a coding sequence, codon CGC is 12
times more likely than codon AGG
– An ORF preferring CGC over AGG is likely
to be a gene
Codon Usage in Human Genome
Codon usage
• One way to test if an ORF is a gene is to
compute
– Pr(ORF sequence under a coding sequence
model)
– Pr(ORF sequence under a non-coding model)
– Ratio of the two.
• These methods work best in prokaryotes
• The exon-intron trouble is not handled yet
Promoter Structure in Prokaryotes
(E.Coli)
Transcription starts
at offset 0.
• Pribnow Box (-10)
• Gilbert Box (-30)
• Ribosomal
Binding Site (+10)
Ribosomal Binding Site
Splicing Signals: an additional
statistical clue, for eukaryotes
Exons are interspersed with introns and
typically flanked by GT and AG
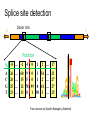
Splice site detection
Donor site
5’
3’
Position
%
A
C
G
T
-8 … -2 -1
26
26
25
23
…
…
…
…
0
1
2
… 17
60 9 0 1 54 … 21
15 5 0 1 2 … 27
12 78 99 0 41 … 27
13 8 1 98 3 … 25
From lectures by Serafim Batzoglou (Stanford)
Consensus splice sites
Statistical approaches:
summary
• Codon usage
• Promoter motifs
• Ribosome binding site
• Splicing sites
Similarity based approaches
Similarity based approaches
• Some genomes may be very well-studied,
with many genes having been
experimentally verified.
• Closely-related organisms may have
similar genes
• Unknown genes in one species may be
compared to genes in some closelyrelated species
The basic approach
• Given a protein sequence, and a genomic sequence,
find a set of substrings of the genomic sequence
whose concatenation best fits the protein sequence
• Deals with the exon-intron problem
• First cut: Find fragments in the genomic sequence
that match portions of the protein sequence (local
alignment)
• Then find the “optimal” subset of non-overlapping
fragments
Exon chaining
• Each of the fragments of the genomic
sequence that somewhat match the protein
(locally) is a putative exon
• The “goodness” of the match is the “weight”
assigned to this putative exon
• Thus, we have a set of weighted intervals
(l,r,w): for a fragment from l to r, with weight w
representing how well it matches (a portion
of) the protein
Exon Chaining Problem
• Input: A set of weighted intervals (l,r,w)
• Output: A maximum weight chain of
non-overlapping intervals from this set
Exon Chaining Problem: Graph Representation
edge from every li to ri
edge between every two successive vertices
21
• This problem can be solved with dynamic
programming in O(n) time.
Assumptions
• No two intervals have a common
boundary point. So the (li,ri) define 2n
distinct points, if there are n intervals
Exon Chaining Algorithm
ExonChaining (G, n) //Graph, number of intervals
for i ← to 2n
si ← 0
for i ← 1 to 2n
if vertex vi in G corresponds to right end of the
interval I
j ← index of vertex for left end of the interval I
w ← weight of the interval I
si ← max {sj + w, si-1}
else
si ← si-1
return s2n
Not very helpful
• A chain is a set of non-overlapping
exons in order (left to right)
• But the matching protein portions may
not be in the same order !
Spliced Alignment
• Begins by selecting either all putative exons
between potential acceptor and donor sites or by
finding all substrings similar to the target protein
(as in the Exon Chaining Problem).
• This set is further filtered in a such a way that
attempt to retain all true exons, with some false
ones.
• Then find the chain of exons such that the
sequence similarity to the target protein
sequence is maximized
Spliced Alignment Problem: Formulation
• Input: Genomic sequences G, target
sequence T, and a set of candidate
exons (blocks) B.
• Output: A chain of exons Γ such that
the global alignment score between Γ*
and T is maximized
Γ* - concatenation of all exons from chain Γ
Dynamic programming
• Genomic sequence G = g1g2…gn
• Target sequence T = t1t2…tm
• As usual, we want to find the optimal
alignment score of the i-prefix of G and
the j-prefix of T
• Problem is, there are many i-prefixes
possible (since multiple blocks may
include position i)
Idea
• Find the optimal alignment score of the
i-prefix of G and the j-prefix of T
assuming that this alignment uses a
particular block B at position i
• S(i, j, B)
• For every block B that includes i
Recurrence
If i is not the starting vertex of block B:
• S(i, j, B) =
max { S(i – 1, j, B) – indel penalty
S(i, j – 1, B) – indel penalty
S(i – 1, j – 1, B) + δ(gi, tj) }
If i is the starting vertex of block B:
• S(i, j, B) =
max { S(i, j – 1, B) – indel penalty
maxall blocks B’ preceding block B S(end(B’), j, B’) – indel penalty
maxall blocks B’ preceding block B S(end(B’), j – 1, B’) + δ(gi, tj)
}