Download How grid cells neurons encode rat position

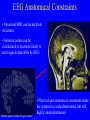
dMEC Neurons firing
Black trace is the rat’s trajectory.
Red dots are spikes recorded from one
neuron.
Eventually a hexagonal activity
pattern emerges.
Different Phases and Spacings
Different spacings
Same length scale,
different phases
Additional Properties
• Reorient when a cue-card is rotated
• Maintain coherence (for a time) in the dark
• Retain spacing independent of enclosure size
Multiple Lattice Sizes
Dramatically Increase Range
Properties of Grid Cells
Update individual lattices independently (parallel math)
Store information combinatorially (like a decimal or binary
number)
Are potentially vulnerable to large errors from small
fluctuations in any lattice
•Errors can be “corrected” with help from extra lattices
The combined information from
the different phases
Optimizing
Some parameters of the system are difficult to measure directly,
but can be addressed theoretically.
Neurons are costly to grow and maintain, therefore we expect
the number of neurons to be minimized for given capability.
R Range
Nn # Neurons
N L # Lattices
n p # Phases
n s # Cells / site
So, can write number of neurons in terms of other variables,
and minimize:
Optimizing cont...
The number of cells per site is set by the need to have a
statistically significant difference in the number of counts
when comparing
-A rat running over an activity blob
-A rat running a past a blob (at the resolution limit)
We model the firing rate as constant background plus gaussian
blobs:
After fitting these constants, we can obtain expressions for
the optimal number of cells per site.
Fit Results
The system is noisy, but by analysing spatial
correlations between pairs of spikes, there are enough
counts to fit parameters confidently.
Data from Fits
•
There is a (noisy) linear
relationship between width of the
blobs and length of the grids
•
Blob Width ~ 0.22 * Grid Length
•
Because width scales linearly
with length, the lattices all have
the same precision in phase
Conclusions from optimization
• The optimal lattices are very imprecise
– Each has O(10) grid cells
– Each has roughly 4 distinct phases in 2D
• By pooling this imprecise information, the
potential range is huge. Ten lattices can
cover 1 square km of range, with an accuracy
of ~20 cm while running.
How do the grid cells work?
Neural sheet
“Mexican Hat”
• Nearby cells excite
• Medium distance cells inhibit
• A hexagonal pattern
spontaneously emerges
Real space
•Head direction cells bias
activity to drift depending on
direction the rat faces
•A hexagonal pattern on neural
sheet results in hexagonal
pattern in real space
Neural Imaging and Signal
Analysis
The goal of neural imaging/signal
analysis is to measure temporal and
spatial activity patterns non-invasively.
• High temporal and spatial resolution
is desirable.
• No single technology currently
satisfies both of these requirements.
• By combining data from different
modalities, the shortcomings of
individual techniques can be overcome.
fMRI
fMRI measures changes in blood
oxygen level (which correlates
with activity) in the brain volume
• Spatial resolution is a few mm
• Temporal resolution is a 2-3 sec,
much lower than desirable
fMRI Technology Solution:
Somehow increase the temporal resolution of fMRI?
• Difficult to do
• Ultimately not useful: the blood oxygen level changes slowly in
response to activity
 The bold signal changes over the course of several seconds
 A high temporal resolution fMRI over-samples a smooth curve
?
EEG
EEG measures changes in voltage at
roughly 100 leads placed on the scalp
• Activity within the bulk must be
inferred
• Spatial resolution is low, the problem
is highly underdetermined
• Temporal resolution is a few ms
EEG Constraints
To obtain a unique solution, EEG solutions are “regularized”,
that is an additional constraint is added. Typical constraints
are:
• Maximal smoothness
• Minimum norm
However these constraints are not well-motivated, and may
actually exclude valid solutions.
EEG Anatomical Constraints
• Structural MRI can locate brain
structures
• Solution points can be
constrained to locations likely to
emit signals detectible by EEG
Solution points confined to gray matter
• Physical and anatomical constraints make
the system less underdetermined, but still
highly underdetermined.
EEG Technology Solution:
Add more leads?
• Impractical: we’d want ~10K leads.
• Still miss signals: EEG measures a superposition of fields from
irrotational sources. Some signals are always undetectable.
• Not useful: simulations indicate that adding more than ~100 leads
doesn’t significantly improve spatial resolution of inferred sources.
Statistical Solution:
When performing EEG source localization, use fMRI as a source
of priors.
• Confine EEG localization to
be in active regions from fMRI
• fMRI signal changes slowly,
so it can be interpolated
Solution will have:
• Spatial resolution of fMRI
• Temporal resolution of EEG