Download A self-organizing model of disparity maps in the primary visual cortex

A self-organizing model of disparity
maps in the primary visual cortex
TIKESH RAMTOHUL
(S0566072)
MASTER OF SCIENCE
SCHOOL OF INFORMATICS
UNIVERSITY OF EDINBURGH
2006
ABSTRACT
Current models of primary visual cortex (V1) development show how visual features
such as orientation and eye preference can emerge from spontaneous and visually
evoked neural activity, but it is not yet known whether spatially organized maps for
low-level visual pattern disparity are present in V1, and if so how they develop. This
report documents a computational approach based on the LISSOM model that was
adopted to study the potential self-organizing aspect of binocular disparity. It is among
the first studies making use of computational modelling to investigate the topographical
organization of cortical neurons based on disparity preferences.
The simulation results show that neurons develop phase disparities as a result of the
self-organizing process, but that there is no apparent orderly grouping based on
disparity preferences. However there seems to be a strong correlation between disparity
selectivity and orientation preference. Neurons exhibiting relatively large phase
disparities tend to prefer vertical orientations. This leads to suggest that cortical regions
grouped by orientation preferences might be subdivided into compartments that are in
turn organised based on disparity selectivity.
i
ACKNOWLEDGEMENTS
I would like to thank Jim Bednar for his help and support throughout this endeavour.
Thank you for your insightful comments and your patience. My sincere thanks also goes
to Chris Ball who has contributed a lot to my understanding of the Python language and
the Topographica simulator. A big thank you also to all the friends I’ve made during
my stay in Edinburgh. The camaraderie has been most soothing, especially during
stressful situations. And finally, thank you Mom and Dad for always being there for
your son.
ii
DECLARATION
I declare that this thesis was composed by myself, that the work contained herein is my
own except where explicitly stated otherwise in the text, and that this work has not been
submitted for any other degree or professional qualification except as specified.
(Tikesh RAMTOHUL)
iii
TABLE OF CONTENTS
CHAPTER 1 INTRODUCTION ............................................................................................... 1
1.1 MOTIVATION ..................................................................................................................................1
1.1 TASK DECOMPOSITION ................................................................................................................2
1.2 THESIS OUTLINE ............................................................................................................................2
CHAPTER 2 BACKGROUND .................................................................................................. 3
2.1 BASICS OF VISUAL SYSTEM........................................................................................................3
2.1.1 EYE .............................................................................................................................................3
2.1.2 VISUAL PATHWAY..................................................................................................................4
2.1.3 RETINA ......................................................................................................................................4
2.1.4 LGN.............................................................................................................................................5
2.1.5 PRIMARY VISUAL CORTEX ..................................................................................................6
2.2 DISPARITY .......................................................................................................................................7
2.2.1 GEOMETRY OF BINOCULAR VIEWING ..............................................................................7
2.2.2 ENCODING OF BINOCULAR DISPARITY ............................................................................9
2.2.3 DISPARITY SENSITIVITY OF CORTICAL CELLS.............................................................10
2.2.4 CHRONOLOGICAL REVIEW ................................................................................................12
2.2.5 Ohzawa-DeAngelis-Freeman (ODF) ENERGY MODEL (1990) .............................................14
2.2.6 ENERGY MODEL: READ et al (2002)....................................................................................16
2.3 TOPOGRAPHY ...............................................................................................................................17
2.3.1 TOPOGRAPHY AND DISPARITY .........................................................................................18
2.3.2 TS’O, WANG ROE and GILBERT (2001)...............................................................................19
2.4 SELF-ORGANIZATION .................................................................................................................20
2.5 COMPUTATIONAL MODELS ......................................................................................................20
2.5.1 KOHONEN SOM......................................................................................................................21
2.6 LISSOM ...........................................................................................................................................22
2.6.1 LISSOM ARCHITECTURE .....................................................................................................23
2.6.2 SELF-ORGANIZATION IN LISSOM .....................................................................................26
2.7 TOPOGRAPHICA ...........................................................................................................................26
2.7.1 MAP MEASUREMENT IN TOPOGRAPHICA ......................................................................27
2.8 MODEL OF DISPARITY SELF-ORGANIZATION ......................................................................28
2.8.1 WIEMER ET AL (2000) ............................................................................................................29
CHAPTER 3 METHODOLOGY ............................................................................................ 32
3.1 SELF-ORGANIZATION OF DISPARITY SELECTIVITY ...........................................................32
3.1.2 TWO-EYE MODEL FOR DISPARITY SELECTIVITY .........................................................32
3.1.3 DISPARITY MAP MEASUREMENT .....................................................................................35
3.1.4 TYPE OF INPUT ......................................................................................................................38
3.2 PHASE INVARIANCE....................................................................................................................39
3.2.1 TEST CASES FOR ODF MODEL ...........................................................................................41
CHAPTER 4 RESULTS ........................................................................................................... 44
4.1 GAUSSIAN......................................................................................................................................45
4.1.1 DETERMINATION OF DISPARITY THRESHOLD..............................................................45
4.1.2 RECEPTIVE FIELD PROPERTIES AND DISPARITY MAPS..............................................47
4.2 PLUS/MINUS ..................................................................................................................................53
4.2.1 DETERMINATION OF DISPARITY THRESHOLD..............................................................53
4.2.2 RECEPTIVE FIELD PROPERTIES AND DISPARITY MAPS..............................................55
4.3 NATURAL.......................................................................................................................................62
4.4 PHASE INVARIANCE....................................................................................................................64
CHAPTER 5 DISCUSSION..................................................................................................... 66
5.1 RECEPTIVE FIELD STRUCTURE ................................................................................................66
5.2 DISPARITY AND ORIENTATION PREFERENCE......................................................................67
5.3 ORIENTATION PREFERENCE AND PHASE DISPARITY ........................................................69
iv
5.4 VALIDATION AGAINST BIOLOGICAL DATA .........................................................................76
5.4.1 DISTRIBUTION OF PHASE DISPARITIES...........................................................................76
5.4.2 DISPARITY AND ORIENTATION PREFERENCE...............................................................77
5.5 SUMMARY .....................................................................................................................................77
CHAPTER 6 CONCLUSION AND FUTURE WORK ......................................................... 79
6.1 CONCLUSION ................................................................................................................................79
6.2 FUTURE WORK .............................................................................................................................80
6.2.1 PHASE INVARIANCE.............................................................................................................80
6.2.2 DISPARITY SELECTIVITY AND OCULAR DOMINANCE................................................83
6.2.3 VERTICAL DISPARITY..........................................................................................................83
6.2.4 PRENATAL AND POSTNATAL SELF-ORGANIZATION...................................................84
BIBLIOGRAPHY ..................................................................................................................... 85
v
CHAPTER 1
INTRODUCTION
1.1 MOTIVATION
An extremely remarkable function of the visual system is the perception of the world in
three-dimensions although the image cast on the retinas is only two-dimensional. It is
believed that the third dimension, depth, is inferred from the visual cues in the retinal
images, the most prominent one being binocular disparity (Qian, 1997). Humans and
other animals possess two eyes whose range of vision overlap. Objects within the
overlapping region project slightly different images on the two retinas. This is referred
to as disparity and it is believed to be one of the cues that the brain uses for assessing
depth.
Although recent studies of binocular disparity at the physiological level have brought
much insight to the understanding of the role of stereopsis in depth perception, much
experimental work remains to be done to eventually yield a unified account of how the
actual mechanism operates. Trying to unlock the mysteries of the brain by relying solely
on biological data is practically impossible. This is where computational models of the
brain come into the picture. They can provide concrete, testable explanations for
mechanisms of long-term development that are difficult to observe directly, making it
possible to link a large number of observations into a coherent theory. It is essential that
the models are based on real physiological data in order to understand brain functions
(Qian, 1997).
One such computational model is LISSOM (Laterally Interconnected Synergetically
Self-Organizing Map), a self-organizing map model of the visual cortex. It models the
structure, development, and function of the visual cortex at the level of maps and their
connections. Current models of the primary visual cortex (V1) development show how
visual features such as orientation and eye preference can emerge from spontaneous and
visually-evoked activity, i.e. there are groups of neurons across the surface of the cortex
which respond selectively to different types of orientation and ocular dominance. But it
is not known if spatially organized maps for disparity are present in V1, and if so, how
they develop. The main aim of the project was to investigate the potential selforganizing feature of disparity selectivity.
1
1.1 TASK DECOMPOSITION
The project was broken down into 2 main stages. The first one dealt with the
investigation of the input-driven self-organization process when disparate retinal images
are used as input. This consisted of developing an appropriate LISSOM model for
disparity and the implementation of suitable map measuring techniques to illustrate
differences in disparity selectivity. The second stage was concerned with the
investigation of possible ways to integrate or simulate complex cells in LISSOM so that
the self-organizing process becomes phase-independent and hence better suited for
disparity selectivity. Current versions of LISSOM develop phase maps when
anticorrelated inputs are used, for e.g. when positive and negative Gaussian inputs are
fed onto the retina. This is quite a predictable outcome since LISSOM develops
behaviour reminiscent of simple cells, and these cells are sensitive to the phase of the
input stimulus. But real animals do not have such maps in V1. One reason might be
because most cells in real animals are complex, and hence insensitive to phase. Thus,
integration of complex cells in the LISSOM structure could lead to formation of selforganized maps that are independent of phase.
1.2 THESIS OUTLINE
The thesis has been divided into 6 chapters, starting with this introductory chapter. The
remaining chapters are organised as follows:
•
Chapter 2 gives an overview of the visual system, describes the key points about
research on binocular disparity, talks about the self-organizing process and
presents related work on computational modelling of disparity.
•
Chapter 3 describes the methodology used for investigating the self-organizing
process of disparity preferences in LISSOM.
•
Chapter 4 presents the simulation results, giving a brief account of the direct
observations.
•
Chapter 5 provides a discussion based on the simulations, validating the
computational results with biological findings where necessary.
•
Chapter 6 highlights the major outcomes from the study on disparity, and
provides a guide to possible extensions to this research work.
2
CHAPTER 2
BACKGROUND
This chapter presents background material required for a good understanding of the
neural processes involved in disparity encoding. Moreover, the self-organizing process
is discussed thoroughly, together with the importance of computational modelling in
neuroscience. The main components of LISSOM are highlighted to provide a clear
image of how topographic maps form using this model. The chapter also includes
related work on disparity models.
2.1 BASICS OF VISUAL SYSTEM
The human visual system is a biological masterpiece that has been faceted and refined
by millions of years of evolution. Its efficiency is unparalleled in comparison with any
piece of apparatus ever invented. It interprets the information from visible light to build
a three-dimensional representation of the world. This section briefly describes the
prominent constituents of the visual system and outlines the neural mechanisms
involved during visual processing.
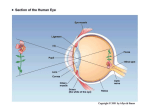
2.1.1 EYE
Light entering the eye is refracted as it passes through the cornea. It then passes through
the pupil, whose size is regulated by the dilation and constriction of the iris muscles, in
order to control the amount of light entering the eye. The lens is responsible for
focusing light onto the retina by proper adjustment of its shape.
Figure 2.1: Anatomy of the human eye (reprinted from [26])
3
2.1.2 VISUAL PATHWAY
The main structures involved in early visual processing are the retina, the lateral
geniculate nucleus of the thalamus (LGN), and the primary visual cortex (V1). The
initial step of the processing is carried out in the retina of the eye. Output from the
retina of each eye is fed to the LGN, at the base of each side of the brain. The processed
signals from the LGN are then sent to V1. V1 outputs are then fed to higher cortical
areas where further processing takes place. The diagram below gives a schematic
overview of the visual pathway
Figure 2.2: Visual Pathway (reprinted from [40])
2.1.3 RETINA
The retina is part of the central nervous system. It is located on the inside of the rear
surface of the eye. It consists of an array of photoreceptors and other related cells to
convert the incident light into neural signals. The retinal output takes the form of action
potentials in retinal ganglion cells whose axons collect in a bundle to constitute the
optic nerve.
The light receptors are of two kinds, rods and cones, being responsible for vision in dim
light and bright light respectively. Rods are more numerous than cones but are
conspicuously absent at the centre of the retina. This region is known as the fovea and
represents the centre of fixation. It contains a high concentration of cones, thereby
making it well-suited for fine-detailed vision.
As mentioned earlier, the output of the retina is represented by the activity of the retinal
ganglion cells. An interesting feature of these cells, which is shared by other neurons
higher up in the visual pathway, is their selective responsiveness to stimuli on specific
spots on the retina. The term ‘receptive field’ is used to explain this phenomenon.
4
Stephen Kuffler was the first to record the responses of retinal ganglion cells to spots of
light in a cat in 1953(Hubel, 1995). He observed that he could influence the firing rate
of a retinal ganglion by focusing a spot of light on a specific region of the retina. This
region was the receptive field (RF) of the cell. Levine and Shefner (1991) define a
receptive field as an “area in which stimulation leads to a response of a particular
sensory neuron”. For a retinal ganglion cell or any other neuron concerned with vision,
the receptive field is that part of the visual world that influences the firing of that
particular cell; in other words, it is that region of the retina which receives stimulation ,
consequently altering the firing rate of the cell being studied.
Most retinal ganglion cells have concentric (or centre-surround) RFs. The latter are of
two types, ON-centre cells and OFF-centre cells. These RFs are divided into 2 parts
(centre/surround), one of which is excitatory ("ON"), the other inhibitory ("OFF"). For
an ON-centre cell, a spot of light incident on the inside (centre) of the receptive field
will increase the discharge rate, while light falling on the outside ring (surround) will
suppress firing. The opposite effect is observed for OFF-centre cells. Other cells may
have receptive fields of different shapes. For example, the RFs of most simple cells in
V1 can have a two-lobe arrangement, favouring a 45-degree edge with dark in the upper
left and light in the lower right, and a three-lobe pattern, favouring a 135-degree white
line against a dark background (Miikkulainen et al, 2005)
Figure 2.3: Receptive Fields (reprinted from [40])
2.1.4 LGN
The LGN receives neural signals from the retina, and sends projections directly to the
primary visual cortex, thereby acting as a relay. Its role in the central nervous system is
not very clear, but it consists of neurons that are very similar to the retinal ganglion
cells. These neurons are arranged retinotopically. Retinotopy or topographic
representation implies that as we move along the retina from one point to another, the
corresponding points in the LGN trace a continuous path (Hubel, 1995). The ON-centre
cells in the retina connect to the ON cells in the LGN and the OFF cells in the retina
connect to the OFF cells in the LGN. Both groups of cells share a common
5
functionality, namely that of performing some sort of edge detection on the input
signals.
2.1.5 PRIMARY VISUAL CORTEX
ARCHITECTURE
The primary visual cortex, situated at the rear of the brain, is the first cortical site of
visual processing. Just like the LGN, V1 neurons also exhibit retinotopy, but they have
altogether different characteristics and functionalities as compared to their geniculate
counterparts. To begin with, most V1 neurons are binocular, displaying a strong
response to stimuli from either eye. They also respond selectively to certain features
such as spatial frequency, orientation and direction of movement of the stimulus.
Interestingly, disparity has also been identified as one of the visual cues that cause
selective discharge in V1 cells. The architecture of V1 is such that at a given location, a
vertical section through the cortical sheet consists of cells that have more or less similar
feature preferences. In this columnar model, nearby columns tend to have somewhat
matching preferences while more distant columns show a greater degree of
dissimilarity. Moreover, preferences repeat at regular intervals in every direction, thus
giving rise to a smoothly varying map for each feature (Miikkulainen et al, 2005).For
example, as we move parallel to the surface of V1, there are alternating columns of
cells, known as ocular dominance columns, which are driven predominantly by inputs
to a single eye. Another type of feature map is the orientation map, which describes the
orientation preference of cells changing gradually from horizontal to vertical and back
again as we move perpendicular to the cortical surface.
TYPE OF CELLS
Another important point about V1 which is relevant to this project concerns the type of
cells that can be found. Hubel and Wiesel(1962) subdivided the cortical cells into 2
main groups, simple and complex, based on their RFs. Simple cells often have a twolobe or three-lobe RF (shown in figure 2.3) . Consider a simple cell with a three-lobe
RF, with an ON region flanked by OFF regions. If a bar of light, with the correct
orientation, is incident on the middle region, the firing rate of the cell will increase, but
if the image is incident on the OFF regions, the firing rate will be suppressed. On the
other hand if a dark bar is incident on the ON region, suppression will take place,
whereas excitation will occur if it falls into the OFF regions of the RF. Thus, the
response of simple cells is dependent on the phase of the stimulus. In contrast, the
response of complex cells does not depend on the phase of the stimulus; spikes will be
elicited if the bar, whether dark or bright, is incident on any region within its receptive
field as long as it is properly oriented.
6
2.2 DISPARITY
We are capable of three-dimensional vision despite having only a 2-D projection of the
world on the retina. This remarkable ability might be just a mundane task for the visual
system but it has baffled many researchers for decades. No wonder then that much
effort has been put in by the scientific community to understand the processes taking
place in the brain during depth perception. It is now known that the sensation of depth is
based upon many visual cues (Qian, 1997), for example occlusion, relative size,
perspective, motion parallax, shading, blur, and relative motion (DeAngelis, 2000;
Gonzales and Perez, 1998). Such cues are monocular, but species having frontally
located eyes are additionally subjected to binocular cues, an example of which is
binocular disparity. It refers to differences between the retinal images of a given object
in space, and arises because the two eyes are laterally separated. Three-dimensional
vision based on binocular disparity is commonly referred to as stereoscopic vision.
Although monocular cues are sufficient to provide the sensation of depth, it is the
contribution of stereopsis that makes this process so effective in humans (Gonzales and
Perez, 1998)
2.2.1 GEOMETRY OF BINOCULAR VIEWING
Suppose that an observer fixes his gaze on the white sphere Q (refer to figure 2.4);
fixation by default causes images of the object to fall on the fovea. We say that QR and
QL are corresponding points on the retinas. The black sphere S is closer to the observer,
and as can be deduced easily by geometry, its images fall at non-corresponding points
in the retinas. Similarly, a point further away from the point of fixation will give images
closer to each other compared to corresponding points. Any such lack of
correspondence is known as disparity.
Figure 2.4:Geometry of Stereopsis( adapted from [57])
7
The distance z from the fixation point, which basically represents the difference in
depth, can be deduced from the retinal disparity δ = r-l and the interocular distance I
(Read, 2005). Such a disparity which is directly related to the location of an object in
depth is known as horizontal disparity.
All points that are seen as the same distance away as the fixation point (Q in this case)
are said to lie on the horopter, a surface whose exact shape depends on our estimations
on distance, and hence on our brains (Hubel, 1995). Points in front and behind the
horopter induce negative and positive disparities respectively. The projection of the
horopter in the horizontal plane across the fovea is the Vieth-Muller circle, which
represents the locus of all points with zero disparity (Gonzales and Perez, 1998)
Figure 2.5:Horizontal disparity( reprinted from [14])
Another type of disparity, much less studied but generally accepted to play some role in
depth perception, is vertical disparity. When an object is located closer to one eye than
the other, its image is slightly larger on the retina of that eye. This gives rise to vertical
disparities. Bishop (1989) points out that such disparities occur when objects are viewed
at relatively near distances above or below the visual plane, but which do not lie on the
median plane (a vertical plane through the midline of the body that divides the body into
right and left halves). This can be best explained by an illustration, given in figure 2.6.
Suppose we have a point P which is above the visual plane and to the right of the
median plane, such that it is nearer to the right eye. Simple geometrical intuition shows
that the angles β1 and β2 subtended by P are different and that β2 > β1. The vertical
disparity v is given by the difference in the 2 vertical visual angles, such that v = β2 - β1
(Bishop, 1989)
8
Figure 2.6: Vertical disparity reprinted from [6])
2.2.2 ENCODING OF BINOCULAR DISPARITY
We have seen that disparity is about the difference between the 2 retinal projections of
an object, but how do cortical cells encode this information? There are 2 models that
have been forwarded, the position difference model and the phase difference model. Let
us assume a Gabor-shaped RF for a binocular simple cell in V1. In the position
difference model, the cell has the same RF profile on each eye but with an overall
position shift between the right and left RFs, i.e. the RF profiles have identical shape in
both eyes but are centred at non-corresponding points on the 2 retinas. In the phase
difference model, the RFs are centred at corresponding retinal points but have different
shapes or phases. Figure 2.7 illustrates the differences between position and phase
encoding.
(a) Position Difference Model
(b) Phase Difference Model
Figure 2.7: Disparity encoding( reprinted from [2])
9
There is evidence that supports each of these two encoding schemes. Position disparity
was demonstrated first by Nikara et al (1968), and later by Joshua and Bishop (1970),
von der Heydt et al (1978) and Maske et al (1984). Evidence of the phase disparities has
also been shown by various studies (DeAngelis et al., 1991, 1995; DeValois and
DeValois, 1988; Fleet et al., 1996; Freeman and Ohzawa, 1990; Nomura et al., 1990;
Ohzawa et al., 1996; Qian, 1994; Qian and Zhu, 1997; Zhu and Qian, 1996)
2.2.3 DISPARITY SENSITIVITY OF CORTICAL CELLS
The two mains groups of cortical cells, namely simple and complex, differ in the
complexity of their behaviour. Hubel and Wiesel (1962) proposed a hierarchical
organisation in which complex cells receive input from simple cells, which in turn
receive input from the LGN. In this model, the simple cells have the same orientation
preference and their RFs are arranged in an overlapping fashion over the entire RF of
the complex cell (Hubel, 1995). They suggested that the complex cells would only fire
if the connections between the simple cells and the complex cell are excitatory and the
input stimuli are incident on specific regions of the RF. This model is not unanimous
among neurophysiologists since some studies have shown that some complex cells have
direct neural connections with the LGN (Qian, 1997). Research in this area has been
very active and there is a much better understanding of the properties of these cells
nowadays, especially in the role they might play in disparity encoding. It is generally
accepted that most simple and complex cells are binocular, i.e. they have receptive
fields in both retinas and show a strong response when either eye is stimulated.
Furthermore, researchers are unanimous over the disparity selectivity of these cells; they
respond differently to different disparity stimuli. These two properties are essential for
disparity computation.
It is therefore tempting to conclude that both types of cell are suitable disparity
detectors, but this is not the case since they have quite distinct characteristics. Receptive
fields of simple cells consist of excitatory (ON) and inhibitory (OFF) subregions that
respond to light and dark stimuli respectively. Complex cells, on the other hand,
respond to stimuli anywhere within their RFs for both bright and dark bars because of a
lack of separate excitatory and inhibitory subregions in the receptive fields (Skottun et
al, 1991). The following diagram illustrates typical RF types for complex and simple
cells. Complex cells generally have larger RFs and respond to targets even if the
contrast polarity is altered (for example, if we replace the black dots with the white dots
and vice-versa). Simple cells have discrete RF subregions and respond when the correct
input configuration is incident on their RFs.
10
Figure 2.8: 1-D RF for simple and complex cells (reprinted from [47])
Ohzawa and collaborators (1990) describe simple cells as “sensors for a multitude of
stimulus parameters” because besides responding to disparity, they also respond
selectively to stimulus position, contrast polarity, spatial frequency, and orientation. On
the contrary, disparity encoding in complex cells is independent of stimulus position
and contrast polarity; changes in irrelevant parameters would therefore not affect the
disparity encoding features of such cells (Ohzawa et al, 1990). The diagram below
shows how the binocular RF of a simple cell changes with lateral displacement of the
stimulus, whereas the complex cell has an elongated RF along the position axis, making
it a better disparity detector. Note that a binocular RF is generated by plotting the
response of the cell as a function of the position of the stimulus in each eye. The
stimulus used is typically a long bar at the preferred orientation of the cell.
Figure 2.9: Binocular RF for simple and complex cells (reprinted from [57])
11
2.2.4 CHRONOLOGICAL REVIEW
The first major contribution to the study of neural mechanisms in binocular vision came
from Barlow et al in the 1960’s. They found out that neurons fire selectively to objects
placed at different stereoscopic depths in the cat striate cortex (Barlow et al, 1967). A
few years later, Poggio and Fischer (1977) confirmed these findings when they
investigated awake behaving macaque monkeys. The visual system of these animals
resembles that of humans (Cowey and Ellis, 1967; Farrer and Graham, 1967; Devalois
and Jacobs, 1968; Harweth et al., 1995), and several studies have led to the conclusion
that they have characteristics of stereopsis similar to humans (Gonzales and Perez,
1998). Using solid bars as stimuli, Poggio and Fischer identified 4 basic types of
neurons, namely tuned-excitatory, tuned-inhibitory, near and far. Tuned-excitatory
neurons discharge best to objects at or very near to the horopter, i.e. zero disparity;
tuned inhibitory cells respond at all disparities except those near zero; near cells are
more responsive to objects that lie in front of the horopter, i.e. to negative disparities,
and finally far cells prefer objects that are behind the horopter, i.e positive disparities
(DeAngelis, 2000)
The invention of the random dot stereogram (RDS) by Julesz (1971) also contributed
largely to this field. A random dot stereogram is a pair of two images of randomly
distributed dots that are identical except that a portion of 1 image is displaced
horizontally (figure 2.10).
Figure 2.10: RDS reprinted from [57])
It looks unstructured when viewed individually, but under a condition of binocular
fusion, the shifted region jumps out vividly at a different depth (Qian, 1997). Several
experiments based on solid bars and RDS provided results that strengthened the notion
of 4 basic categories of disparity-selective neurons being present (Gonzales and Perez,
12
1998). A few reports also mention the presence of 2 additional categories, namely tuned
near and tuned far (Poggio et al, 1988; Gonzales et al, 1993a), combining the properties
of tuned excitatory cells with those of near and far cells respectively. Figure 2.11
illustrates the disparity tuning curves for the 6 categories of cells obtained from
experiments on the visual cortex of monkeys carried out by Poggio et al (1988) .TN
refers to tuned near cell, TE to tuned excitatory, TF to tuned far, NE to near, TI to
tuned inhibitory, and FA to far.
Figure 2.11: Disparity Tuning Curves (reprinted from [24])
Amidst all these exciting findings, a proper mathematical approach to simulate
disparity-selectivity of cortical cells failed to emerge (Qian, 1997). In 1990 however,
Ohzawa, DeAngelis and Freeman proposed the disparity energy model to simulate the
response of complex cells. The latter has been widely accepted as a very good model of
the behaviour of disparity-selective cells in V1. The next section gives an in-depth
description of this interesting approach. However, results obtained from some
physiological studies have not been in phase with certain of its predictions. In an
attempt to account for these discrepancies, Read et al (2002) came up with a modified
version of the original energy model. The basic features of Read’s model are also
highlighted in this chapter.
13
2.2.5 Ohzawa-DeAngelis-Freeman (ODF) ENERGY MODEL (1990)
In an earlier section, certain properties of complex cells have been highlighted that
make them well-suited for disparity encoding. To recap, the interesting features of these
cells include selectivity to different stimuli disparities, an indiscriminate response to
contrast polarity and an apparent insensitivity to stimulus position. Ohzawa and
colleagues postulate that these are not enough to create a suitable disparity detector.
They outline 3 additional properties that need to be taken into account to develop a
suitable algorithm. These are:
1. The disparity selectivity of complex cells must be much finer than that predicted
by the size of the RFs, as reported by Nikara et al (1968)
2. The preferred disparity must be constant for all stimulus positions within the RF
3. Incorrect contrast polarity combinations should be ineffective if presented at the
optimal disparity for the matched polarity pair, i.e. a bright bar to one eye and a
dark bar to the other should not give rise to a response at the preferred disparity
The authors explain the purpose of the first 2 requirements by an illustration shown in
the figure 2.12. Figure 2.12(a) shows the RF of a cortical neuron in image space on left
and right eye retinas. The hatched diamond-shaped zone represents the region viewed
by both eyes. Any stimulus within this zone should elicit a response from the neuron in
question. But this implies that the neuron is limited to crude disparity selectivity since
this region encompasses many different disparities (Ohzawa et al, 1990). A disparity
detector should be more specific, i.e. it should respond to a restricted range of visual
space. In this example, if we assume that the 2 eyes are fixated on an object (meaning
zero disparity), then the dark-shaded oval region represents a suitable zone. A graphical
representation of this region is shown in figure 2.12(b). The diagonal slope represents a
plane of zero disparity. The 2 axes represent stimulus positions along the left eye and
right eye. For nonzero disparity, the sensitive region for a detector must be located
parallel to and off the diagonal.
The third requirement deals with “mismatched contrast polarity” (Ohzawa et al, 1990).
Recall that complex cells exhibit phase independence since they are insensitive to
contrast polarity. The question that arises is whether a disparity detector should respond
if anti-correlated stimuli are presented to the eyes at the correct disparity (for e.g., a
bright bar to one eye and a dark one to the other). This is a theoretically implausible
scenario because images on the retinas are from the same object, so there is no question
14
of getting a bright spot in 1 part of one of the retinas and a dark spot in the
corresponding part of the other retina (Ohzawa et al, 1990), but in a computational
framework, this is very likely to happen, especially with RDS as inputs. Ohzawa and
colleagues classify this requirement as a “non-trivial” one and suggest that it is
“counterintuitive to expect the detector to reject anti-correlated stimuli at the correct
disparity on the basis of mismatched contrast polarity”
Figure 2.12: Desired characteristics of a disparity detector (reprinted from [45])
Taking into account all the aforementioned requirements, Ohzawa and collaborators
devised the disparity energy model. It consists of 4 binocular simple cell subunits that
can be combined to produce the output of a complex cell. The inputs from the 2 eyes are
combined to give the output of each subunit. The resulting signal is then subjected to a
15
half-wave rectification followed by a squaring non-linearity. The response of the
complex cell is given by combining the contribution from each subunit.
The authors postulate that the simple cell subunits must meet certain requirements to
produce a smooth binocular profile. These are as follows:
•
They must have similar monocular properties like spatial frequency, orientation,
size and position of the RF envelopes
•
They must share a common preferred disparity
•
The phases of the four simple cells must differ from each other by multiples of
90 (quadrature phase)
•
The RFs for the simple cells must be Gabor-shaped
•
The simple cells must be organised into “push-pull” pairs, i.e., the RFs in 1
simple cell are the inverses of those in the other simple cell; in other words, the
ON region of 1 cell corresponds to an OFF region in the other.
The schematic diagram in figure 2.13 shows the ODF model for a tuned-excitatory
neuron. S1 and S2 form 1 push-pull pair while S3 and S4 form the other. Members in a
push-pull pair are mutually inhibitory (Ohzawa et al, 1990).
Figure 2.13:ODF Disparity Energy Model( reprinted from [47])
2.2.6 ENERGY MODEL: READ et al (2002)
This model is very similar to the previous model except that the half-wave rectification
is performed on the inputs from each eye before they converge on a binocular cell. This
16
thresholding is achieved by introducing the monocular cells as shown in figure 2.14 and
the authors claim that this alteration gives results close to real neuronal behaviour when
anticorrelated inputs are used. The model also emphasizes on the type of synapses the
monocular cells make with the binocular neurons to account for inhibitory effects of
visual stimuli observed during biological experiments.
Figure 2.14: Modified Energy Model (reprinted from [58])
2.3 TOPOGRAPHY
The topographic arrangement of the primary visual cortex and the presence of cortical
feature maps were highlighted in a previous section. The maps are superimposed to
form a hierarchical representation of the input features. This type of representation was
suggested by Hubel and Wiesel (1977). They postulated that orientation and OD maps
are overlaid in a fashion so as to optimize the uniform representation of all possible
permutations of orientation, eye preference and retinal position (Hubel and Wiesel,
1977). Subsequent studies making use of optical imaging techniques have helped to
justify this claim of superimposed, spatially periodic maps being present in the cortex,
and also to strengthen the views formulated by Hubel and Wiesel about the geometrical
relations between feature maps (Swindale, 2000).
In addition to orientation and OD columns in the cortex, maps for direction of motion
and spatial frequency have also been observed (Hubener et al, 1997; Shmuel and
Grinvald, 1996; Welliky et al, 1996) have also been observed. The following question
comes to one’s mind: Do spatially periodic maps for other features that influence
neuronal behaviour exist? It is a well-known fact that cortical cells respond to a
17
multitude of visual feature attributes, so there exists the possibility of corresponding
feature maps to be present in the cortex. It is only through delicate biological
experiments using state-of the art imaging techniques that clear-cut results can be
obtained.
2.3.1 TOPOGRAPHY AND DISPARITY
Studies on stereoscopic vision have so far focused more on the physiology of simple
and complex cells and their role in encoding disparity. Very few studies have
concentrated on the topographic arrangement of disparity-sensitive neurons in V1.
Blakemore (1970) initially proposed that ‘constant depth’ columns can be found in the
cat V1 (DeAngelis, 2000). He advocated that such columns consist of neurons having
similar receptive-field position disparities. But due to the unsophisticated experimental
setup and lack of substantial experimental data, his findings were not deemed good
enough to comprehensively resolve this issue.
Another study conducted by LeVay and Voigt (1988) showed that “nearby V1 neurons
have slightly more similar disparity preferences than would be expected by chance”
(DeAngelis, 2000), although , as DeAngelis (2000) points out, the clustering was not as
definite as in the case of orientation selectivity or ocular dominance. Moreover, most of
the neurons that were investigated were near the V1/V2 border, thereby weakening the
claim of V1 having disparity-selective columns (DeAngelis, 2000).
Most work in this area has shifted to looking for these maps in higher areas of the
cortex, and recent research conducted by DeAngelis and Newsome (1999) has provided
some evidence for a map of binocular disparity in the middle temporal (MT, also known
as V5) visual area (DeAngelis and Newsome, 1999) of macaque monkeys by using
electrode penetrations. They found discrete patches of disparity-selective neurons
interspersed among other patches showing no disparity sensitivity. They claim that the
preferred disparity varies within the disparity-tuned patches and that disparity columns
exist in the MT region, and possibly in V2, since MT receives input connections from
V2. This is an interesting finding but yet not conclusive enough to prove the existence
of spatially periodic disparity maps. Reliable results can only be obtained if a large
population of neurons can be measured at once, for example by using optical imaging
techniques. Experiments using such a procedure have actually been conducted by Ts’o
et al (2001). They combined optical imaging, single unit electrophysiology and
cytochrome oxidase (CO) histology to investigate the structural organization for colour,
form (orientation) and disparity of area V2 in monkeys. The findings from this
18
endeavour might be of great relevance to the investigation of disparity maps in the
brain, hence the need for a separate subsection to describe the prominent features of this
research work.
2.3.2 TS’O, WANG ROE and GILBERT (2001)
Previous work on primates using CO histology has shown that V2 has a hierarchical
organization reminiscent of that found in V1, except that cells are compartmentalised
based on orientation-selectivity, colour preference and disparity selectivity. Two main
types of alternating CO-rich stripes have been observed, the thick and thin stripes that
are often separated by a third type commonly referred to as the pale stripe (Tootell and
Hamilton, 1989). The thick stripe is believed to contain cells selective to disparity and
motion, the thin stripe seems to be responsive to colour preferences, and the pale stripe
is associated with orientation selectivity. Ts’o and colleagues performed various
experiments by using a combination of techniques that included optical imaging,
electrode penetrations and CO histology for increased effectiveness and reliability. The
first set of tests provided results that seemed to justify the tripartite model of visual
processing in V2 that was put forward by earlier research work. They found unoriented,
colour-selective cells in the thin stripes, and of greater interest to this project, cells that
are selective to retinal disparity in the thick stripes. These cells were unselective to
colour, and had complex, oriented RFs (Ts’o et al, 2001).They also observed that these
cells showed little or no response to monocular stimulation but responded vigorously to
binocular stimuli over a small range of disparities. In order to get a better distinction
between the arrangement of the colour and disparity stripes, they subjected the primates
to monocular stimulation, the idea being that disparity-selective regions would not be
responding. The expected result of clear-cut delineation between the disparity and
colour stripes was not observed, leading the authors to suggest the existence of
subcompartments within the V2 stripes. Based on this type of hierarchical organisation
in V2, they draw a parallel with that of V1, which also contains subcompartments,
although mention is not made of the presence of disparity stripes in V1. Other relevant
observations along disparity stripes concern the orientation preference and type of
disparity-selective cells. It was seen that most of the cells had vertical or near vertical
preferred orientation. They found out that within a disparity stripe, most of the columns
contained cells of the tuned excitatory type but that columns populated with the other 3
types of cells were also present. The authors conclude that “one key functional role of
area V2 lies in the establishment of a definitive functional organisation and cortical map
for retinal disparity”.
19
2.4 SELF-ORGANIZATION
How does the brain develop such distinctive characteristics? Researchers believe that
these maps form by the self-organization of the afferent connections to the cortex and
are shaped by visual experience (Miikkulainen et al, 2005), based on cooperation and
competition between neurons as a result of correlations in the input activity (Sirosh and
Miikkulainen ,1993). As research in this field intensified, it became clear that selforganization is not influenced by these afferent connections alone, but also by lateral
connections parallel to the cortical surface (Miikkulainen et al, 2005). Based on various
observations, Miikuulainen and collaborators believe that the wiring of the lateral
connections is not static but rather develops “synergetically and simultaneously” with
the afferent connections, based on visual experience. These researchers describe the
adult visual cortex as a “continuously adapting recurrent structure in a dynamic
equilibrium, capable of rapid changes in response to altered visual environments”
(Miikkulainen et al, 2005). This implies that the functional role of the afferent and
lateral connections is to suppress redundant information in the input stimuli, while being
able to learn correlations found in novel visual features. This type of organization that
relies heavily on visual features is termed as Input-Driven Self-Organization.
If self-organization depends heavily on the types of inputs presented, then what about
the influence of genetic factors in the arrangement of neurons in the brain? The previous
discussion might mislead the reader in thinking that cortical maps develop solely as a
result of visual activity after birth. Experimental findings tend to show that this is not
the case. Indeed, it is believed that both genetic and environmental factors affect the
topography of the cortex. In the prenatal stage, internally generated activity such as
retinal waves and Ponto-Geniculo-Occipital(PGO) waves are thought to be genetically
specified training patterns that initiate the self-organizing process. Studies have shown
that animals have brain regions showing orientation selectivity even before birth
(Miikkulainen et al, 2005), thereby strengthening the hypothesis of geneticallydetermined internal signals in initiating the self-organizing process. Thus, an organism
already has a basic topographic framework at birth, and this organization is constantly
refined by visually-evoked activity after birth.
2.5 COMPUTATIONAL MODELS
Neuroscience has been the focus of extensive research for a very long time, but
researchers are not even close to come up with a unified account of on-going neural
mechanisms and processes. The sheer complexity of the brain has so far proved to be an
20
overwhelming hurdle although, to be fair, considerable headway has been made in
many research areas.
The setting up of biological experiments requires lots of time and effort, consequently
making progess in neuroscience slow and painful. For quite some time now, scientists
have adopted a new approach to research, namely computational modelling. This has
provided a new dimension to studies related to the brain and has been embraced by
many researchers. Computational models can be used instead of biology, as concisely
described by Miikkulainen et al (2005), “to test ideas that are difficult to establish
experimentally, and to direct experiment to areas that are not understood well”.
(Miikkulainen et al, 2005). Ohzawa and colleagues (1990) point out that these models
play an important role in neuroscience since they can provide quantitative predictions
that may be compared with results from biological experiments (Ohzawa et al, 1990).
Because of these attractive features, it is unsurprising that computational neuroscience
has been used to investigate the self-organizing process.
Ever since von der Malsburg (1973) pioneered this area of research by using a twodimensional network of neural units to model the cortex, several other models have
been proposed (Miikkulainen et al, 2005). However most of these models did not cater
for the dynamic nature of the lateral connections (Miikkulainen et al, 2005), and
therefore might not be ideal to simulate the self-organizing process. More recent models
have inevitably focused more on the dynamicity of the visual cortex with increased
emphasis on the interaction between the afferent and lateral connections (Miikkulainen
et al, 2005). The model of interest for this project is LISSOM, proposed by
Miikkulainen and colleagues. Section 2.6 describes the hierarchical and functional
properties of this model. It is based on the simple but effective self-organizing feature
map (SOM) model proposed by Kohonen (1982b). The next section gives a brief
overview of this famous algorithm.
2.5.1 KOHONEN SOM
SOM maps a high-dimensional input data space onto a two-dimensional array of
neurons. In the context of our study, the latter represents the cortical surface whereas
the former refers to a receptor surface such as the retina. Every unit in the neural sheet
is connected to all the units on the receptor surface, such that all the cortical units
receive the same input stimuli. So if we have a retina of N units, each neuron will have
an input vector of length N. Each connection has a positive synaptic weight. Since each
neuron is connected to N inputs, it will have a weight vector of length N associated with
21
it. The neuron computes its initial response as a function of the Euclidean distance
between the input and the weight vectors. A winner-take-all process usually operates
whereby the cortical neuron with the highest activation affects the activity of the nearby
neurons based on a neighbourhood function. The weight vector is modified using the
Euclidean difference between the input and the weight vectors. Initially the connection
weights are random, such that each neuron responds randomly to activity on the retina.
During learning, the weights adapt, slowly making each neuron more specific to
particular input patterns. Consequently, the weight vectors become better
approximations of the input vectors, and neighbouring weight vectors become more
similar. After many iterations, the weight vectors become an ordered map of the input
space, thereby leading to retinotopy.
2.6 LISSOM
LISSOM stands for Laterally Interconnected Synergetically Self-Organizing Map. It is
a learning algorithm designed to capture the essence of the self-organizing process in
the visual cortex by concentrating on certain processes that have been overlooked by
most computational models, more specifically the influence of the lateral connections.
Miikkulainen et al (2005) perceive LISSOM as a model that can give concrete, testable
answers to the following viewpoints:
1. input-driven self-organization is responsible to shape up cortical structures
2. self-organization is influenced by inputs that are internally generated, as a result
of the genetic blueprint of an organism, as well as visually-evoked activity from
the environment
3. perceptual grouping, i.e. the process of finding correlations in the input stimuli
to successfully and coherently identify an object in the visual scene, is a
consequence of the interaction between afferent and lateral connections
LISSOM is inspired from various studies that have been conducted on the selforganizing process and from data collected about the structure of the cortex. It was
developed in an attempt to model neurobiological phenomena and yield results that may
inspire new research directions. The salient features of LISSOM, as described by
Miikkulainen and collaborators (2005) are given below:
1. the neural sheet is a two-dimensional array of computational units, each unit
corresponding to a vertical column in the cortex
2. each cortical unit received input from a local anatomical receptive field in the
retina, usually with the ON-centre and OFF-centre channels of the LGN as
intermediate sheets between the input and output sheets
22
3. interactions between afferent and lateral connections govern the input-driven
self-organizing process
4. each cortical unit has a weight vector whose length is determined by the number
of connections; it responds by computing a weighted sum of its input
5. learning is based on Hebbian adaptation with divisive normalization, which is
the computational equivalent of the biological learning procedure
The following sections describe the LISSOM model in more detail. Most of the material
is taken from Chapter 3 in ‘Computational Maps in the Visual Cortex’ (CMVC) book
by Miikkulainen and colleagues (2005).
2.6.1 LISSOM ARCHITECTURE
The architecture of the basic LISSOM model is shown in figure 2.15. Each V1 neuron is
connected to a bunch of neurons in the LGN-ON and LGN-OFF sheets. In LISSOM
jargon, the term connection field is used to refer to a region in a lower-level sheet that
has direct connections with a neuron in a layer hierarchically on top of the other one.
Thus each cortical neuron is connected to specific regions in the LGN layer. This is
unlike the SOM model, wherein each cortical neuron is fully connected to the lower
layer. The LGN neurons in turn have connection fields onto the retina. Each neuron
develops an initial response as a weighted sum of the activation in its afferent input
connections. The lateral connections translate the initial activation pattern into a
localized response on the map. After a settling period, the connection weights of cortical
neurons are modified through Hebbian learning. As the self-organizing process
progresses, activity bubbles are produced that become increasingly focused and
localized. The result is a self-organized structure in a dynamic equilibrium with the
input.
Figure 2.1 : Architecture for basic LISSOM model(reprinted from [40])
23
RETINA
The retinal sheet is basically an array of photoreceptors that can be activated by the
presentation of input patterns. The activity χxy for a photoreceptor cell (x,y) is calculated
according to
where (xc,k , yc,k) specifies the centre of Gaussian k and σu its width
LGN
The connection weights of the LGN neurons are set to fixed strengths using a
difference-of-Gaussians model (DoG). There is a retinotopic mapping between the LGN
and the retina. The weights are calculated from the difference of two normalized
Gaussians; weights for an OFF-centre cell are the negative of the ON-centre weights,
i.e. they are calculated as the surround minus the centre. The weight Lxy,ab from receptor
(x, y) in the connection field of an ON-centre cell (a, b) with centre (xc, yc) is given by
where σc determines the width of the central Gaussian and σs width of the surround
Gaussian.
The cells in the ON and OFF channels of the LGN compute their responses as a
squashed weighted sum of activity in their receptive. Mathematically the response ξab of
an LGN cell (a,b) is computed by
where χxy is the activation of cell (x, y) in the connection field of (a, b), Lxy,ab is the
afferent weight from (x, y) to (a, b), and γL is a constant scaling factor. The squashing
function σ is a piecewise linear approximation of a sigmoid activation function
24
CORTEX
The total activation is obtained by taking both the afferent and lateral connections into
account .First, the afferent stimulation sij of V1 neuron (i, j) is calculated as a weighted
sum of activations in its connection fields on the LGN:
where ξab is the activation of neuron (a, b) in the receptive field of neuron (i, j) in the
ON or OFF channels, Aab,ij is the corresponding afferent weight, and γA is a constant
scaling factor. The afferent stimulation is squashed using the sigmoid activation
function. The neuron’s initial response is given as as
where σ (·) is a piecewise linear sigmoid
After the initial response, lateral connections influence cortical activity over discretized
time steps. At each of these time steps, the neuron combines the afferent stimulation s
with lateral excitation and inhibition:
where ηkl(t-1) is the activity of another cortical neuron (k, l) during the previous time
step, Ekl,ij is the excitatory lateral connection weight on the connection from that neuron
to neuron (i, j), and Ikl,ij is the inhibitory connection weight. The scaling factors γE and γI
represent the relative strengths of excitatory and inhibitory lateral interactions.
Connections to the cortex are not set to fixed strengths as it is the case with the LGN
connections. Weight adaptation of afferent and lateral connections is based on Hebbian
learning with divisive postsynaptic normalization. The equation is as given below
25
where wpq,ij is the current afferent or lateral connection weight from (p, q) to (i, j),
w’pq,ij is the new weight to be used until the end of the next settling process, α is the
learning rate for each type of connection, Xpq is the presynaptic activity after settling,
and ηij stands for the activity of neuron (i, j) after settling
2.6.2 SELF-ORGANIZATION IN LISSOM
Orientation maps have been widely investigated using computational modeling.
LISSOM has also focused extensively on the topographic arrangement of cortical
neurons based on orientation preference. The figure below shows the organization of
orientation preferences before and after the self-organizing process
Iteration 0
Iteration 10,000
Figure 2.16 : Orientation map in LISSOM(reprinted from [40])
2.7 TOPOGRAPHICA
The Topographica simulator has been developed by Miikkulainen and collaborators to
investigate topographic maps in the brain. It is perpetually being refined and extended
in an attempt to make it as generic as possible and to promote the investigation of
biological phenomena that are not very well understood. This study on disparity
necessitated the addition of some new functionalities in Topographica, especially for
the generation of disparity feature maps. The next section highlights the map
measurement techniques currently used in Topographica.
26
2.7.1 MAP MEASUREMENT IN TOPOGRAPHICA
There are various algorithms that can be used for feature map measurement. Most of
these techniques produce similar results, especially in cases where neurons are strongly
selective for the feature being investigated, but might yield different results for units
that are less selective (Miikkulainen et al, 2005).There are typically two types of
methods, namely direct and indirect, that can be used to compute preference maps. In
direct methods, maps can be calculated directly from the weight values of each neuron,
while indirect methods involve presenting a set of input patterns and analyzing the
responses of each neuron. The choice of map measurement technique usually implies a
tradeoff between efficiency and accuracy, since direct methods are more efficient while
indirect methods are more accurate (Miikkulainen et al, 2005). In Topographica both
methods have been used to calculate feature maps. For example, the map of preferred
position is obtained by computing the centre of gravity of each neuron’s afferent
weights, whereas orientation maps are calculated by an indirect method called the
weighted average method, introduced by Blasdel and Salama (1986). The next section
gives a detailed account of this method. It is based almost entirely from material in
Appendix G.1.3 of the CMVC book.
WEIGHTED AVERAGE METHOD
In the weighted average method, inputs are presented in such a way so as to ensure that
a whole range of combinations of parameter values is possible. For each value of the
map parameter, the maximal response of the neuron is recorded. The preference of a
neuron corresponds to the weighted average of the peak responses to all map parameter
values. This may sound somewhat confusing; it’s better to clarify this by describing this
method mathematically and subsequently giving an example of its application. The
following subsection does just that.
Consider the weighted average method being used to compute orientation preferences.
For each orientation φ, parameters such as spatial frequency and phase are varied in a
systematic way, and the peak response η̂ φ is recorded. A vector with length η̂ φ and 2φ
as its orientation is used to encode information about each orientation φ. The vector
V= (Vx , Vy) is formed by summing up the vectors for all the orientation values.
27
The preferred orientation of the neuron, θ is estimated as half the orientation of V :
where atan2(Vx , Vy) returns tan-1(Vx / Vy) with the quadrant of the result chosen based
on the signs of both arguments. Orientation selectivity can be obtained by taking the
magnitude of V. This can be normalized for better comparison and analysis purposes.
Normalized orientation selectivity, denoted by S, is given by:
As an illustration, suppose that input patterns were presentation at orientation 0°, 60°
and 120°, and phases 0, π/8, …, 7π/8 for a total of 24 patterns. Assume that the peak
responses for a given neuron for all the different phases were 0.1 for 0°, 0.4 for 60° and
0.8 for 120°. The preferred orientation and selectivity of this neuron are
The interesting point to note here concerns the selectivity value for this neuron. It has a
relatively low selectivity because it responds quite well to patterns with different
orientations, namely 60° and 120°. High selectivity would therefore indicate a strong
bias towards one particular value of a feature parameter.
2.8 MODEL OF DISPARITY SELF-ORGANIZATION
Although numerous models for self-organization have been put forward, very few have
actually been customized to investigate the topographic arrangement of neurons based
on disparity preferences. This is quite surprising since the presence of disparity maps in
V1 based on biological data is yet to be confirmed, and therefore computational
neuroscience would have been ideal to help scientists channel their research on
predictions made by the model. Anyway, one such work was undertaken by Wiemer et
al (2000).
28
2.8.1 WIEMER ET AL (2000)
The aim of their research was to investigate the representation of orientation, ocular
dominance and disparity in the cortex. Since orientation and OD maps have been widely
studied using both computational and traditional neuroscience techniques, the emphasis
of their work was more on the potential presence of disparity map in the cortex. They
used the SOM algorithm for learning. Nothing really extraordinary, one might say, but
what really made their work distinctive are the methods employed for presenting input.
In an earlier section, the importance of the input stimuli in the self-organization process
has been made clear. Wiemer and colleagues stress on the significance of the types of
binocular stimuli to be presented in order to have any chance of getting clumps of
disparity-selective neurons. They generate such stimuli by first creating a threedimensional scene, and then take stereo pictures of it. According to the authors, this
kind of processing preserves the correlations between stimuli features such as
orientation and disparity. Further processing includes cutting the pictures in ocular
stripes, and aligning them in alternating order to produce a fused projection. The whole
fused image is not presented as the input stimulus. Instead, chunks of it that contain
features from both the left and right ocular stripes are selected based on the amount of
correlation between them. The algorithm rejects any chunk that contains very little
correlation between the part from the left ocular stripe and that from the right ocular
stripes. This is done to ascertain that the left and right-eyed part correspond to the same
three-dimensional object (Wiemer et al, 2000). The selected chunks represent the
binocular stimuli that will be presented to the network. They are normalized to ensure
that dissimilarities in brightness of different pairs of stereo images do not affect the final
results.
Figure 2.17 (reprinted from [69]): A and B represent the stereo images obtained from
the three-dimensional scene. These images are divided into stripes, which are arranged
in alternating order to form the image shown in C. Chunks of this image are then
selected based on the amount of correlation to yield the pool of stimuli, shown in D, to
be presented to the network.
29
The results obtained by Wiemer and collaborators are shown in figures 2.18 and 2.19
Figure 2.18 shows maps of left-eyed and right-eyed receptive fields. It can be seen that
RFs of different shapes and asymmetries are present with pools of neurons preferring
similar patterns varying gradually along the two-dimensional grid (Wiemer et al, 2000).
Fig 2.18 : Maps of left-eyed and right-eyed receptive fields(reprinted from [69])
Figure 2.19 shows the resulting binocular feature representation obtained by the fusion
of the left- and right-eyed receptive fields. The corresponding orientation, ocular
dominance and disparity maps are illustrated. One interesting point that can be clearly
distinguished when analyzing maps B and D in figure 2.19 is that disparity differences
are greatest in regions of vertical and oblique orientations (Wiemer et al, 2000). The
white patches in D represent positive disparities; black patches indicate negative
disparities, while gray is for zero or very small disparities. Based on these results, the
authors suggest that subcompartments corresponding to different disparities might exist
in regions of constant orientation, such that maps of orientation, ocular dominance and
disparity might be geometrically related.
The study by Wiener and colleagues is an intriguing one to say the least. Their
conclusion about disparity patches lying within regions of relatively uniform orientation
preference has been proved to be true by the experiments conducted by Ts’o et al on the
V2 region of the macaque monkey. But there are certain reservations about the validity
of their model. First, the authors do not mention anything about which region of the
visual cortex they are simulating, thereby casting doubts over specificity of their
experiment. Moreover, they don’t use the concept of overlapping receptive fields that is
a distinctive feature of cortical neurons, which might be important for self-organization.
In addition, the manner in which binocular stimuli are presented is quite debatable
although the algorithm used to extract such stimuli from a three-dimensional scene is
30
impressive. It seems that they use the notion of a ‘cyclopean’ eye to process the
binocular stimuli instead of having two eyes with slightly disparate images incident on
them. Next, if the maps are analyzed, serious discrepancies seem to be present as
compared to the ones found in biology: The neurons do not have the usual centresurround, two-lobed or three-lobed RF that is so characteristic of cortical neurons; the
orientation map is far from showing any kind of periodicity. Despite these apparent
imperfections, this model is one of the first to probe into the existence of disparity
maps, and therefore the effort by Wiemer et al is worth some consideration.
Figure 2.19 : Binocular Feature Representation(reprinted from [69])
31
CHAPTER 3
METHODOLOGY
This chapter is divided into 2 main sections. The first one highlights the methods used
to investigate self-organization of disparity maps in. The second one describes the work
done in an attempt to solve the problem of phase-dependent behaviour of current
LISSOM models.
3.1 SELF-ORGANIZATION OF DISPARITY SELECTIVITY
At the onset of the project, the Topographica software did not have the desired
functionality to investigate the potential self-organizing feature of disparity selectivity.
Therefore the first major task was to understand the intricacies of the simulator to be
able to provide the appropriate experimental setup for the inspection and measurement
of disparity preferences and selectivities. More specifically, the first requirement
consisted of developing a network based on two retinas, with suitable input patterns on
each one, to simulate the input-driven self-organizing process that is believed to
culminate into disparity selectivity in the primary visual cortex of primates. The second
major task was about development of a map measurement mechanism to compute the
disparity preferences of the cortical units. The following sections give a detailed
account of how these two tasks were tackled
3.1.2 TWO-EYE MODEL FOR DISPARITY SELECTIVITY
Most studies using LISSOM have been based on a single eye, although two retinas have
been used before to investigate ocular dominance. However the experiments on eye
preferences were conducted in the C++ version of LISSOM. There was no tailor-made
Topographica script that dealt with two eyes. So the first and perhaps the most
important aspect of the project was to come up with a model that could reliably simulate
the self-organization process. The starting point and inspiration was the lissom_oo_or.ty
script that can be found in the examples folder of the topographica directory. It is used
to investigate orientation selectivity based on a single retina and LGN ON/OFF
channels. The model for this simulation is illustrated in figure 3.1.
32
Figure 3.1: Model used in lissom_oo_or.ty
As can be seen from the illustration, the model consists of an input sheet (‘Retina’), an
LGN layer (‘LGNOff’ and ‘LGNOn’), and an output sheet (‘V1’). The connections from
the retina to the LGN (‘Surround’ and ‘Centre’) are based on the difference-ofGaussians (DoG) model. The afferent connections, namely ‘LGNOffAfferent’ and
‘LGNOnAfferent’, regulate the activation of neurons in the neural sheet. Lateral
connections are also included; they are represented as the dotted yellow circles in ‘V1’.
Another important point concerns the type of input pattern. This model makes use of
elongated Gaussians. They are generated randomly across the input space, and their
orientations are also determined by a random process. The idea is to ensure that each
receptor in the input sheet is subjected to all possible position-orientation permutations
when the simulation is run for a large number of iterations, so that a smooth orientation
map can develop. It is to be noted that the values used for the parameters in this model
are based on those that were used in the LISSOM C++ experiments for orientation
selectivity. Interested readers can check out Appendix A in CMVC book to get a general
idea of how the correct values can be chosen for the simulation parameters.
Based on the single-eye model, it was relatively straightforward to design the skeleton
for a two-eye model. It consists of two input sheets, two LGN ON/OFF channels and
one output sheet. The number of afferent connections is doubled as expected. The
diagram below sums it all. Initially, the values used for the parameters were the same as
33
in the single-retina model; but later on, some of them had to be tweaked, as shall be
explained in subsequent sections
Figure 3.2: two-eye model
The next step consisted of generating input patterns that would be slightly offset in each
eye to simulate horizontal retinal disparity. This was not as easy as setting up the
framework since it required knowledge of some distinct features in Topographica.
Eventually this was successfully achieved. The figure below shows a simulation
scenario in which the input patterns are offset by 12 units (the retinal size is 54 units
along the horizontal axis).
Figure 3.3: elongated Gaussians as input
A prototypical model to investigate disparity selectivity was now ready. Not quite,
actually. The main criterion to judge whether the parameters in the model had been
34
correctly set was by comparing the orientation maps obtained while using the
lissom_oo_or.ty script and the disparity model for the case of zero disparity. They
should be giving identical maps. This was not the case and clearly indicated that
something was wrong. After much probing, it became obvious that something was
amiss with the activation of neurons in the output sheet. Let us consider the one-eye
case. For a particular input pattern I, let us assume that the activity of a neuron, say N,
due to the afferent connections is x. Then for the case of zero disparity, for pattern I in
each eye, the activity of N due to the afferent connections would be greater than x.
Recall that the activity of a cortical neuron due to its afferent connections is simply a
linear sum of the contribution of all these connections. There are many ways to solve
the problem of this increased level of activity. The simplest one includes using the
strength parameter associated with the connections that is provided by Topographica.
The strength value in the one-eye model was 0.5. By simply halving that value for each
of the afferent connections in the zero disparity models, the desired orientation map was
obtained.
The model was ready for experimentation, except for one last tweak. In the one-eye
model, the weights were initialized randomly. For examples, the LGNOff and LGNOn
connections would have different sets of initial weights. This is not a problem per se,
but for the experiments on disparity, one would want to compare the learned weight
values between the left-eye connections and the right-eye connections. To provide a
convenient platform of comparison, the weights of all the connections were initialized
to the same value. This has very little influence on the final topographic organization.
3.1.3 DISPARITY MAP MEASUREMENT
At the beginning of the project, the necessary functionality to generate orientation maps
was already present in Topographica. The first step in setting up disparity map
measurement therefore consisted of understanding the different classes and functions
that were involved in computing orientation preferences. Once the whole mechanism
became clear, the basic function for measuring disparity was implemented. There are
certain useful points that are worth to be highlighted. The first one concerns the type of
input used. Sine gratings were chosen ahead of other input types for reasons that are
listed below:
•
One input presentation covers the whole input space as compared to inputs such
as elongated Gaussians being used. The latter cover only a small portion of the
retina and are usually used for training instead of map computation. This implies
35
that fewer input presentations are required when sine gratings are used, thus
making the map measurement process faster
•
Sine gratings have a phase component that is very important for disparity
measurement, as discussed below
The second point concerns the type of disparity being measured. In Chapter 2, allusion
was made to two main types of disparity encoding, namely position difference and
phase difference. In the current LISSOM model, it is easier to investigate phase
disparity as a result of the way in which connection fields have been implemented.
Consider a scenario with one input sheet and one output sheet, without any LGN layer.
If a cortical neuron is at position (i,j) in the two-dimensional output sheet, then its
connection field will also be centred at position (i,j) in the retina, thereby maintaining
retinotopy. Now if two input sheets are used, our neuron will have its connection field
centred at corresponding points in each retina. Recall that in the position difference
model, a cortical neuron has its receptive fields at non-corresponding points on each
retina whereas for the phase model, the RFs are at corresponding points. Thus LISSOM
is better suited to investigate phase disparity, although the current implementation can
be altered to make it suitable for the investigation of position disparity.
Since phase disparity is to be measured, one important factor, namely periodicity, has to
be taken into account when using the weighted average method. Phase is a periodic
parameter, and therefore averaging must be done in the vector domain, as described in
the previous section. Sine gratings are 2π-periodic, therefore phases just above and
below zero(for e.g. 10° and 350°) should average to 0°; for non-periodic parameters
such as ocular dominance, the arithmetic weighted average is used (Miikkulainen et al,
2005). This was already implemented in Topographica, so it was only a matter of using
the right functions.
Yet another point concerns the presentation of the input patterns to two retinas. Some
modifications had to be made to the existing Topographica code to ensure that the
patterns are input properly to both eyes. Taking all these into account, a functionality to
compute disparity maps was implemented. The following parameters were to be varied
systematically, phase and orientation of the sine grating, and the amount of phase
disparity to be present in both eyes. As an example, consider a certain input presentation
where the phase of the sine grating is 0°, the orientation is 90°, and the amount of phase
disparity is 180°. The function computes the new phase of the pattern on the left retina
to be -90° (0° - 180°/2), and that for the right retina as 90° (0° + 180°/2), thereby
maintaining a phase difference of 180° between the two patterns. Note that since phase
is a cyclic property, only values between 0° and 360° are considered, such that values
36
such as -90° are processed to fall into that range (-90° is the same as 270° for a sine
grating). So, for the phase of the input pattern, the range was between 0° and 360°. For
disparity however, the range should be between -180° and 180° instead of 0° to 360°.
This is because disparity has been treated as a signed property in this project and the
convention has been maintained for map measurement purposes as well. A positive
value of disparity would imply the phase of the input pattern in the right eye is greater
than that in the left eye, while a negative value would indicate the opposite. But
eventually the range 0° to 360° was used because of the colour code that was used for
proper visualization of selective regions in the disparity map. Negative values are
clipped to zero during the plotting process, and therefore the range -180° and 180° does
not yield a proper map. When using the range 0° to 360°, it is imperative that a
distinction is made between values from 0° to 180°, and 180° to 360°. Any value, say
x°, in the former range indicates that the phase of the input pattern in the right eye is
greater than that in the left eye by x°. Any value, say y°, in the range 180° to 360°,
indicates that the phase in the left eye is greater than that in the right eye by (360° - y°).
So if we have a phase difference of 300° (phase in right eye is greater than phase in left
eye by 300°), it is the same as a phase difference of -60° (phase in left eye is greater
than phase in right eye by 60°).
A: Or = 90°, Freq =1.2 Hz, LPhase=0°,
RPhase=0°
B: Or = 90°, Freq =1.2 Hz, LPhase=-90°,
RPhase=90°
C: Or = 45°, Freq =2.4 Hz, LPhase=45°,
RPhase=135°
D: Or = 0°, Freq =2.4 Hz, LPhase=45°,
RPhase=90°
Figure 3.4: Sine Gratings
37
Note that the the png file used for the colour code for disparity maps was originally
used for orientation. Readers should not take the orientations of the colour bars into
consideration while analyzing the disparity maps.
Figure 3.5: Colour Code
3.1.4 TYPE OF INPUT
The self-organizing process depends a lot on the type of inputs being presented. It was
therefore imperative to carry out sets of experiments with different types of inputs. The
first set of experiments (referred to as Gaussian) has the usual oriented Gaussians as
input, with all the patterns being brighter than the background The second set (referred
to as Plus/Minus) deals with oriented Gaussians which can be either brighter or darker
than their surround . This required some modifications to the original disparity script
file in order to randomly present bright or dark Gaussian patterns. The final set of
experiments (referred to as Natural) is concerned with the presentation of stereo image
pairs as input. This necessitated the collection of suitable stereo images from the
internet to set up an image database. The script file randomly chooses a pair of stereo
images from the database, applies a window function to select corresponding chunks
from each image and present them as input (see figure 3.6)
38
Left part of stereo image
Right part of stereo image
(a):Pair of Stereo Images
(b):Chunks of Stereo Image presented as input
Figure 3.6 : Natural
3.2 PHASE INVARIANCE
The second stage of the project consisted of finding a means to resolve the phase
invariance issue in LISSOM. The RF profiles developed during LISSOM simulation
correspond to those of simple cells, and this means that they are sensitive to the phase of
their inputs. For example, if the RF of one neuron has an ON-centre flanked by two
OFF regions, it would respond to a bright bar that is correctly oriented, but would not
respond to a dark bar even if it is optimally oriented. It has been mentioned earlier that
complex cells are different from simple cells as far as the phase of the stimulus is
concerned. Complex cells are indeed phase-dependent and therefore are ideally suited
for disparity selectivity, as discussed in Chapter 2. There was a need to probe into this
matter in an attempt to integrate complex cells in LISSOM. Because of its popularity
and simplicity, the ODF model was chosen as a potential inspiration of how phase
invariance can be achieved in LISSOM. This section described the methodology used to
implement and test the ODF model using the functionality in Topographica.
39
Based on the schematic diagram in section 2.2.5 of Chapter 2, the basic framework for
the LISSOM version of the ODF model was implemented. A skeletal view is given in
figure 3.7. It consists of two input sheets (LeftRetina and RightRetina), 4 intermediate
sheets (S1, S2, S3 and S4) cell sub-units, and one output sheet(C).
Figure 3.7 : Skeletal view for ODF model in Topographica
Since the aim was to investigate the output of a single complex cell, a one-to-one
connectivity had to be present between the intermediate sheets and the output sheet.
This means that the each of the intermediate sheets and the output sheet consists of only
one neuron. The intermediate sheets thus correspond to the simple cell sub-units in the
ODF model, and the output sheet corresponds to the complex cell. The next step was to
apply the half-wave rectification and the squaring non-linearity to the output of the
simple cell sub-units. A couple of simple output functions were implemented and
applied to the intermediate sheets. The last step consisted of simulating the RF profiles
of the simple cells. Since receptive field structure is determined by the weight values of
the afferent connections in Topographica, Gabor-shaped weight patterns with the
required 90° phase differences were applied to connections from the input sheets to the
intermediate sheets. The LISSOM-based ODF model was ready for experimentation.
40
3.2.1 TEST CASES FOR ODF MODEL
Once the ODF model was implemented, the next task consisted of setting up some test
cases to understand its behaviour. There are quite a few studies that have been
conducted in the past to investigate this, one of which involved the use of Random Dot
Stereograms as input stimuli. This was carried out by Read et al (2002), and their work
on the energy model is the main inspiration for the test cases in this section. The
interesting point about RDS, as Gonzales and Perez (1998) advocate, is that “they do
not have any monocularly recognizable figure and depth can be perceived only under
strict binocular vision” (Gonzales et al, 1998). It was important to implement this type
of stimulus into Topographica. There are many ways to generate RDS, but since this
work was inspired from the experiments carried out by Read et al, the techniques used
in their study were adopted. The matlab code for generating RDS was provided by
Jenny Read, and it became a case of implementing a Topographica-friendly version of
the code. It was quite tricky to achieve this but in the end, this was successfully done.
The Topographica version allows many parameters to be varied such that a large range
of RDS patterns could be generated. Some of the parameters included horizontal
disparity, vertical disparity, dot density, dot size and random. The random parameter
randomly determines the position of each dot in the retina. The following diagrams
illustrate scenarios for zero, negative, and positive horizontal disparities with a retinal
size of 100*100 units, dot size of 5*5 units, dot density of 50%, and random parameter
set to 500.
(a):Zero Disparity
41
(b):Negative disparity(Near)
Dots move outwards
(c):Positive disparity(Far)
Dots move inwards
Figure 3.8: Random Dot Stereograms
Using the RDS as stimuli, it was hoped that the LISSOM-based ODF model would
yield disparity tuning curves characteristic of the 4 main categories of cells observed in
V1, namely tuned excitatory, tuned inhibitory, near and far. Previous studies have
shown that the ODF model can simulate the response of these 4 types of cells by setting
the correct RF profiles for each simple cell sub-unit. Tables 3.1 to 3.4 give the phases
used for the Gabor-shaped weight patterns associated with the connections between the
retinas and the simple cells.
S1
S2
S3
S4
LeftRetina
0°
180°
90°
270°
RightRetina
0°
180°
90°
270°
Table 3.1: RF profiles for generating tuned excitatory cell
42
S1
S2
S3
S4
LeftRetina
0°
180°
90°
270°
RightRetina
180°
0°
270°
90°
Table 3.2: RF profiles for generating tuned inhibitory cell
S1
S2
S3
S4
LeftRetina
0°
180°
90°
270°
RightRetina
90°
270°
180°
0°
Table 3.3: RF profiles for generating near cell
S1
S2
S3
S4
LeftRetina
90°
270°
180°
0°
RightRetina
0°
180°
0°
270°
Table 3.4: RF profiles for generating far cell
43
CHAPTER 4
RESULTS
This chapter is divided into 4 main sections, the first three illustrating the results
obtained while investigating the self-organizing process using different types of input.
The last section presents the results obtained with the Topographica-based ODF model.
For the Gaussian and Plus/Minus case, it was important to determine a suitable
threshold for the maximum amount of retinal disparity that should be applied to get
reliable results. Since orientation maps have been studied extensively both by using
computational modelling and by optical imaging techniques on animals, it was
reasonable to investigate the effects of disparity on these maps in an attempt to estimate
the aforementioned disparity threshold. It was hoped that within a certain range of
disparities, the OR maps would be more or less similar, and that disparity levels outside
that range would produce some major degradation to the arrangement of the orientationselective patches. The idea was to have the orientation map for the zero disparity case as
a reference, so that it can be compared to the orientation maps obtained when the
amount of disparity is incrementally increased. Once the threshold was determined,
other features like receptive field properties and disparity maps could be investigated
for different levels of retinal disparity. A good way to understand the response of
cortical neurons in LISSOM is to look at the afferent weights after the learning process.
The afferent weights for one neuron represent the retinal pattern that would produce
maximal excitation; therefore these weights are analogous to the receptive fields of the
cortical unit. It is to be noted that a disparity of x retinal units here implies that the
network has been trained by presenting patterns that are offset in each eye by a
maximum value of x; it does not refer to input patterns having a constant retinal
disparity of x. The retina is 54 units wide, and the diameter of the circular connection
field of an LGN neuron is 18 retinal units.
44
4.1 GAUSSIAN
4.1.1 DETERMINATION OF DISPARITY THRESHOLD
(a) : OR maps for zero disparity
(b) : OR maps for disparity of 1.5 units
(c) : OR maps for disparity of 2.0 units
45
(d) : OR maps for disparity of 2.5 units
(e) : OR maps for disparity of 3.0 units
(f) : OR maps for disparity of 4.5 units
Figure 4.1: OR maps for different levels of disparity for Gaussian
COMMENTS
On analyzing these maps, it can be seen that as the amount of disparity is increased,
there is a gradual degradation of the OR maps with respect to the reference map, as
initially predicted. There seems to be an increased preference to horizontal orientations.
Just by eye-balling, it can be estimated that the threshold for maximum retinal disparity
is 2.0 units.
46
4.1.2 RECEPTIVE FIELD PROPERTIES AND DISPARITY MAPS
CASE 1: ZERO DISPARITY
LGNOffLeftAfferent Weights after 20000
iterations, Plotting Density 10.0
LGNOffRightAfferent Weights after 20000
iterations, Plotting Density 10.0
Figure 4.2(a): Receptive fields of left and right eye (Off Afferent)
LGNOnLeftAfferent Weights after 20000
iterations, Plotting Density 10.0
LGNOnRightAfferent Weights after 20000
iterations,Plotting Density 10.0
Figure 4.2(b): Receptive fields of left and right eye (On Afferent)
47
ON
OFF
ON-OFF
Figure 4.2(c): Left-Eye RF of typical neuron (On Afferent-Off Afferent of unit[5][5])
ON
OFF
ON-OFF
Figure 4.2(d): Right-Eye RF of typical neuron (On Afferent-Off Afferent of unit[5][5])
LGNOffRightAfferent Weights - LGNOffLeftAfferent Weights
Plotting Density 10.0
Figure 4.2(e): Difference between left and right RFs (Off Afferent)
48
Disparity Map with original colour code
Map with processed colours
Figure 4.2(f): Disparity Map for zero disparity case
COMMENTS
Figures 4.2(a) and 4.2(b) show the afferent weights from the LGN sheets to the output
sheet for every fifth neuron in each direction. It can be seen that most of the neurons are
selective for orientation, with preferences varying for each of them. For example, in
figure 4.2(b), the second neuron from top left corner has a preferred orientation of
around 90° (vertical), while the fifth one has a preferred orientation of around 0°
(horizontal). The final RF (On-Off) of a typical neuron for either eye is shown in figures
4.2(c) 4.2(d). It has an ON-centre with two flanking OFF lobes. Most of the neurons
seem to have the same three-lobed structure. Figure 4.2(e) shows the difference between
the right-eye weights and the left-eye weights. It clearly indicates that the weights are
identical, showing that the phase disparity between right-eye and left-eye RFs is zero.
This is confirmed by the disparity map shown in figure 4.2(f). It is obvious from these
maps that the cortical neurons have a disparity preference of zero. Note that one version
of the disparity map with inverted colours have also been included for better clarity.
Upon careful observation, it can be seen that there are very faint patches randomly
scattered. This is an artifact of the weighted average method and the coarse granularity
of the colour coding.
49
CASE 2: DISPARITY of 2.0 UNITS
LGNOffLeftAfferent Weights after 20000
iterations, Plotting Density=24.0
LGNOffRightAfferent Weights after 20000
iterations, Plotting Density=24.0
Figure 4.3(a): Receptive fields of left and right eye(Off Afferent)
LGNOffRightAfferent Weights - LGNOffLeftAfferent Weights
Plotting Density=24.0
Figure 4.3(b): Difference between left and right RFs(Off Afferent)
50
Disparity Map with original colour code
Map with inverted colours
Figure 4.3(c): Disparity Map for disparity of 2.0 units
COMMENTS
For better visualization purposes, the afferent weights from the LGN sheets to the
output sheet are plotted for every second neuron in each direction. From figure 4.3(a), it
can be seen that orientation preferences are fairly evenly distributed in the range 0° to
180°. A notable distinction from the zero disparity case is in the difference between the
right-eye and left-eye afferent weights, shown in figure 4.3(b). It indicates that when
some disparity is introduced, phase differences start to appear in the monocular RFs of
the neurons. The disparity map illustrates these differences as well. Faint bluish and
greenish patches are found to be present here and there, hinting that the phase disparities
might range from -30° to 30°. These patches also seem to correspond to regions where
neurons having a preference for vertical or near-vertical orientations are foundA more
detailed account of the properties for this amount of disparity will be given in the next
chapter.
51
CASE 3: DISPARITY of 4.5 UNITS
LGNOffLeftAfferent Weights after 20000
iterations, Plotting Density=24.0
LGNOffRightAfferent Weights after 20000
iterations, Plotting Density=24.0
Figure 4.4(a): Receptive fields of left and right eye(Off Afferent)
LGNOffRightAfferent Weights - LGNOffLeftAfferent Weights
Plotting Density=24.0
Figure 4.4(b): Difference between left and right RFs(Off Afferent)
52
A:Disparity Map with original colour code
Map with inverted colours
Figure 4.4(c): Disparity Map for disparity of 4.5 units
COMMENTS
Figure 4.4(a) depicts the preference for horizontal or near horizontal orientations by
most of the neurons, as illustrated by the orientation map in figure 4.1(f). The
dissimilarity between the right- and left-eyed RFs also seem to be more pronounced, as
shown in figure 4.4(b), with more clear-cut phase differences. The disparity map
corroborates these observations. Both negative and positive phase disparities are wellrepresented, with magnitudes of 90° and above also present.
4.2 PLUS/MINUS
4.2.1 DETERMINATION OF DISPARITY THRESHOLD
(a) : OR maps for zero disparity
53
(b) : OR maps for disparity of 1.5 units
(c) : OR maps for disparity of 2.0 units
(d) : OR maps for disparity of 2.5 units
(e) : OR maps for disparity of 3.0 units
54
(f) : OR maps for disparity of 4.5 units
Figure 4.5: OR maps for different levels of disparity for Plus/Minus
COMMENTS
The first point to note in the Plus/Minus case is that the reference OR map is different
from its Gaussian counterpart. The arrangement for the orientation-selective clumps is
seemingly less smooth. But the increased bias to horizontal orientations as amount of
disparity is increased is also present here. A threshold of 2.0 retinal units seems to be a
safe bet for this set of inputs as well.
4.2.2 RECEPTIVE FIELD PROPERTIES AND DISPARITY MAPS
CASE 1: ZERO DISPARITY
LGNOffLeftAfferent Weights after 20000
iterations, Plotting Density 10.0
LGNOffRightAfferent Weights after 20000
iterations, Plotting Density 10.0
Figure 4.6(a): Receptive fields of left and right eye(Off Afferent)
55
LGNOnLeftAfferent Weights after 20000
iterations, Plotting Density 10.0
LGNOnRightAfferent Weights after 20000
iterations, Plotting Density 10.0
Figure 4.6(b): Receptive fields of left and right eye(On Afferent)
ON
OFF
ON-OFF
Figure 4.6(c): Left-Eye, OFF-Centre RF of neuron [0][3]
ON
OFF
ON-OFF
Figure 4.6(d): Left-Eye, ON-Centre RF of neuron [0][21]
56
ON
OFF
ON-OFF
Figure 4.6(e): Left-Eye, two-lobed RF of neuron [9][10]
LGNOffRightAfferent Weights - LGNOffLeftAfferent Weights
Plotting Density 10.0
Figure 4.6(f): Difference between left and right RFs(Off Afferent)
57
Disparity Map with original colour code
Map with inverted colours
Figure 4.6(g): Disparity Map for zero disparity case
COMMENTS
The striking feature here concerns the type of RF profiles. In contrast to the Gaussian
case where most RFs had the ON-centre three-lobed structure, in the Plus/Minus case,
there are both ON-centre and OFF-centre RFs, as well as two-lobed RFs. This can be
clearly seen in figures 4.6(a)-(e). Otherwise, the disparity characteristics seem to be
similar to the Gaussian zero-disparity case.
CASE 2: DISPARITY of 2.0 UNITS
LGNOffLeftAfferent Weights after 20000
iterations,Plotting Density=24.0
LGNOffRightAfferent Weights after 20000
iterations, Plotting Density=24.0
Figure 4.7(a): Receptive fields of left and right eye(Off Afferent)
58
LGNOffRightAfferent Weights - LGNOffLeftAfferent Weights
Plotting Density=24.0
Figure 4.7(b): Difference between left and right RFs(Off Afferent)
Disparity Map with original colour code
Map with inverted colours
Figure 4.7(c): Disparity Map for disparity of 2.0 units
59
COMMENTS
There seems to be larger and more vivid patches of disparity-selective neurons here than
in the Gaussian case, suggesting a greater range of phase disparities, but probably not
by much. A more detailed analysis will be undertaken in the next chapter.
CASE 3: DISPARITY of 4.5 UNITS
LGNOffLeftAfferent Weights after 20000
iterations, Plotting Density=24.0
LGNOffRightAfferent Weights after 20000
iterations, Plotting Density=24.0
Figure 4.8(a): Receptive fields of left and right eye(Off Afferent)
60
LGNOffRightAfferent Weights - LGNOffLeftAfferent Weights
Plotting Density=24.0
Figure 4.8(b): Difference between left and right RFs(Off Afferent)
Disparity Map with original colour code
Map with processed colours
Figure 4.8(c): Disparity Map for disparity of 4.5 units
61
COMMENTS
The afferent weights show a high bias towards horizontal orientations, just like in the
Gaussian experiment for this level of retinal disparity. The disparity map is quite
different though, in the sense that it spans a much larger range of phase disparities. The
coloured patches suggest that disparities between -180° to 180° are encoded.
4.3 NATURAL
Figure 4.9(a): OR maps for stereo images
LGNOffLeftAfferent Weights after 10000
iterations, Plotting Density 10.0
LGNOffRightAfferent Weights after 10000
iterations, Plotting Density 10.0
Figure 4.9(b): Receptive fields of left and right eye(Off Afferent)
62
LGNOnLeftAfferent Weights after 10000
iterations, Plotting Density 10.0
LGNOnRightAfferent Weights after 10000
iterations, Plotting Density 10.0
Figure 4.9(c): Receptive fields of left and right eye (On Afferent)
Disparity Map with original colour code
Map with processed colours
Figure 4.9(d) : Disparity Map for Stereol Images
COMMENTS
The OR map obtained when chunks of stereo image pairs are used is very messy. This
haphazard organization can be understood when the receptive fields are analyzed. Most
of them do not have well-developed profiles. The familiar two-lobed and three-lobed
RFs are not present. The disparity map is also different from the other disparity maps
investigated previously. There is relatively very little preference for zero disparity, even
when compared to the cases in the Gaussian and Plus/Minus experiments with retinal
disparity of 4.5 units. There is apparently a preference for large phase disparities,
typically those with magnitude higher than 90°.
63
4.4 PHASE INVARIANCE
The simulations for the LISSOM-based model were performed using retinal size of
100*100 units, dot density of 50% and a dot size of 5*5 units. For each experiment, 500
different patterns were presented. The disparity tuning curves obtained for the tuned
excitatory, tuned inhibitory, near and far scenarios are given below. The x-axis
represents the amount horizontal disparity, where 0.1 units correspond to 10 retinal
units. The vertical axis gives the cumulative sum of the activity of the cell after
presentation of 500 different input patterns
(a) Tuned Excitatory
(b) Tuned Inhibitory
(c) Near
(d) Far
Figure 4.10: Disparity Tuning Curves for the 4 different RF configurations
The tuning curves obtained are similar to those observed in biological experiments for
the 4 main types of cells, namely tuned excitatory, tuned inhibitory, near and far (cf.
figure 2.11 in Chapter 2), suggesting that the ODF model was successfully
implemented in Topographica. However, due to time constraints, work on the phase
64
invariance issue had to be curtailed. There is probably a means to integrate the ODF
model into LISSOM to ultimately simulate complex cells, but implementation of such a
scheme would probably require quite some time. Instead, a phase invariant model based
on the trace rule and inspired from previous work by Sullivan and R. de Sa (2004), is
proposed in the Chapter 6. It might serve as a rough guide to how phase invariant
response can be achieved.
65
CHAPTER 5
DISCUSSION
In this project, the effects of retinal disparity on input-driven self-organization have
been investigated using the LISSOM model. This chapter is about the analysis of results
from the different sets of experiments conducted in an attempt to assess the validity of
the model used. Emphasis is laid not only on the computational aspects of the study but
also on the relevance of the results to biological findings in the field of binocular
disparity.
The discussion will focus on the Gaussian and Plus/Minus experiments; whereas the
simulation results based on stereo images will be overlooked. This is because natural
images contain a multitude of features, for example, several different orientations and
different levels of disparity might be present in a single image, and therefore a
systematic analysis of the results is practically impossible.
The phase invariance issue could not be investigated properly, and therefore it is not
addressed in this chapter. However, a model that can potentially achieve phase invariant
response is outlined in Chapter 6.
5.1 RECEPTIVE FIELD STRUCTURE
This section deals with the effect of input types on the receptive field structure. The
results from the experiments have shown that the final receptive field profile depends a
lot on the type of input used for training. The experiments on Gaussians yielded threelobed ON-centre receptive fields, whereas the Plus/Minus experiments produced both
ON and OFF-centre RFs as well as receptive fields with only two lobes.
In the Gaussian experiments, the input patterns are always brighter than the
background. This means that the activity on the LGN ON and OFF sheets will always
have the configuration shown in the figure 5.1, i.e the type of activity shown for the
LGN ON sheets will never be present on the LGN OFF sheets, and vice versa. Thus,
over a large number of learning iterations, the afferent weights to V1 organize in such a
way so as to best match the activity on the LGN sheets, leading to the formation of
three-lobed ON-centre receptive fields.
66
Figure 5.1: Gaussian Inputs (always brighter than background)
In the Plus/Minus experiments, the input patterns can be brighter or darker than the
background, and therefore the LGN activity can have either of the configurations shown
in figure 5.2(a) and 5.2(b). This explains why V1 neurons tend to have both ON-centre
and OFF-centre Gabor-shaped RFs. The interaction between the afferent connections
and the lateral connections also lead to the formation of other types of RF profiles, such
as the two-lobed ones.
(a):Gaussian patterns brighter than background
(b):Gaussian patterns darker than background
Figure 5.2 : Plus/Minus Inputs
5.2 DISPARITY AND ORIENTATION PREFERENCE
On the basis of the results obtained for the Gaussian and Plus/Minus experiments, it was
seen that as the amount of disparity was gradually increased, the preference for
horizontal or near-horizontal orientations conspicuously increased. Conversely, the
preference for vertical or near-vertical orientation seems to decrease drastically,
especially at large retinal disparities. The OR maps clearly show this trend. There is an
explanation for these phenomena. Consider the diagrams shown in figures 5.3(a)-(d)
below. In figure 5.3(a) for instance, each illustration refers to a square section of the
retina with an elongated Gaussian input. The dashed turquoise circle corresponds to the
receptive field of a hypothetical cortical neuron. The receptive fields in both retinas are
67
at corresponding points. Figure (iii) is obtained when figures (i) and (ii) are superposed.
This can be interpreted as the stimulus seen by the neuron when the monocular stimuli
are fused together, as if there is a cyclopean eye. Figures 5.3(a) and 5.3(b) consider a
scenario where the inputs are horizontally oriented while vertical stimuli are
investigated figures 5.3(c) and 5.3(d). In the example, two different retinal disparities
are considered, x and y, where y is greater than x. It can be seen in figures 5.3(a) and
5.3(b), than the fused stimulus falling within the binocular receptive field of the neuron
is more or less the same even when different retinal disparities are used. The binocular
stimulus is a ‘reinforced’ version of the monocular stimuli and thus has considerable
influence on the activation of the neuron and hence on the learning process.
For the vertical case, when the retinal disparity is x units, both input stimuli fall within
the binocular receptive field of the neuron and hence there is considerable activation.
But at a retinal disparity of y, this is no longer the case and the activity of the neuron
due to this set of stimuli is less than before, thereby contributing less towards weight
adaptation. Thus, for the same retinal disparity of y units, this neuron is activated more
if the input patterns have an orientation of 0° than an orientation of 90°. This can
explain the presence of more horizontal-oriented and less vertical-oriented receptive
fields as the amount of disparity is increased.
(i)Left Retina
(ii)Right Retina
(iii)Fused image
Figure 5.3(a): Retinal disparity of x units for a horizontally-oriented input pattern
(i)Left Retina
(ii)Right Retina
(iii)Fused image
Figure 5.3(b): Retinal disparity of y units for a horizontally-oriented input pattern
68
(i)Left Retina
(ii)Right Retina
(iii)Fused image
Figure 5.3(c): Retinal disparity of x units for a vertically-oriented input pattern
(i)Left Retina
(ii)Right Retina
(iii)Fused image
Figure 5.3(d): Retinal disparity of y units for a vertically-oriented input pattern
5.3 ORIENTATION PREFERENCE AND PHASE DISPARITY
The disparity maps in the previous chapter showed the presence of phase disparities
between the left-eye and right-eye receptive fields. This section covers these findings in
more details. The simulations for the Gaussian and Plus/Minus case with a maximum
retinal disparity of 2.0 units would be considered. Emphasis would be laid on the
relationship between orientation preference and disparity, and on the magnitude of these
phase disparities.
The first step of the analysis will focus on the frequency distribution of the phase
disparities and orientations for both the Gaussian and Plus/Minus simulations. The
corresponding histograms are shown in figures 5.4(a)-(d). It can be seen that in both
cases, the modal value is in the region of zero, i.e. there is an overwhelming number of
neurons that prefer phase disparities as close as possible to zero. For the Gaussian
experiment, the maximum negative disparity is -35°, and the maximum positive
disparity is around 29°, while for the Plus/Minus case, the maximum values are -86°
and 41° respectively. The orientation histograms also seem to indicate that there is a
preference for orientations having a significant horizontal component; orientations in
the range between 70° to 130° are much less frequent.
69
Figure 5.4(a): Histogram for phase disparity (Gaussian, retinal disparity of 2.0 units)
Figure 5.4(b): Histogram for orientation (Gaussian, retinal disparity of 2.0 units)
70
Figure 5.4(c): Histogram for phase disparity (Plus/Minus, retinal disparity of 2.0 units)
Figure 5.4(d): Histogram for orientation (Plus/Minus, retinal disparity of 2.0 units)
71
It was observed that phase disparities seemed to be associated with cells preferring
orientations that have a significant vertical component, although reservations have to be
made about this observation since a quantitative analysis was not performed. This
section will deal with such an analysis. A small portion of the cortical sheet will be
considered, a square region of 100 units, corresponding approximately to the enclosed
parts shown below in the disparity maps.
Disparity Map(Gaussian,2.0 units)
Disparity Map(Plus/Minus,2.0 units)
Figure 5.5: Disparity Maps
The phase disparities and orientation preferences for this bunch of neurons, for both the
Gaussian and Plus/Minus simulations with a maximum retinal disparity of 2.0 units are
given in the tables below. The dashed red and blue rectangles enclose clumps of
neurons with a preference for negative and positive disparities respectively. Their
corresponding orientation preferences are also enclosed. It can be seen that in general,
neurons having quite different left-eye and right-eye RF profiles tend to prefer
orientations with a significant vertical component. Scatter plots for phase disparities as a
function of orientation for this bunch of neurons are shown in figures 5.6(e) and 5.6(f).
Note that the absolute value of the disparities is taken, and a similar sort of processing is
done to the orientation values. For example, an orientation of 150° is the same as an
orientation of -30°, and therefore has the same magnitude as an orientation of 30°.
72
-23
-19
-5
4
8
11
6
0
-2
-1
-22
-16
0
9
12
14
6
-6
-13
-13
-9
-1
-1
14
16
16
3
-2
-3
-15
-1
-1
0
0
16
18
-3
-3
-4
-16
-1
-1
0
0
0
3
1
-4
-5
-13
-1
-1
0
0
1
0
0
0
-3
-5
4
6
6
10
11
6
3
2
0
-2
8
9
8
10
10
8
4
3
2
-2
5
4
4
9
11
5
3
2
0
0
-1
-1
3
9
2
0
0
0
0
0
Figure 5.6(a): Disparity preference (in degrees) for a bunch of neurons(Gaussian)
125
112
11
109
100
90
87
75
70
66
105
103
106
103
97
92
94
127
125
97
46
30
34
90
91
91
104
137
135
119
35
17
17
28
66
78
118
136
135
122
34
20
21
26
36
49
179
133
134
117
40
28
27
31
38
35
22
28
60
48
40
44
46
53
54
42
48
56
55
45
46
53
69
77
67
49
52
53
51
36
50
55
67
64
53
46
47
47
42
8
43
40
39
42
40
33
32
34
29
3
Figure 5.6(b): Orientation preference (in degrees) for a bunch of neurons(Gaussian)
73
-13
-17
-12
13
25
24
15
6
3
6
-15
-12
6
18
22
25
10
0
2
3
-18
4
10
16
17
18
12
0
2
2
-10
10
12
14
17
15
-3
-9
1
1
-1
11
11
11
12
14
-16
-24
-11
1
3
7
8
8
9
6
-9
-19
-14
2
3
0
6
6
7
4
1
0
-1
-1
1
1
5
7
8
8
5
4
2
-1
2
-6
3
2
2
9
5
4
1
-1
0
2
2
2
3
0
5
2
0
-3
Figure 5.6(c): Disparity preference (in degrees) for a bunch of neurons(Plus/Minus)
61
67
77
79
82
80
68
36
25
18
72
72
72
86
90
89
75
24
23
18
97
71
78
89
93
93
88
21
16
12
80
63
74
82
88
93
97
163
14
7
55
54
64
69
72
74
96
108
134
1
47
111
53
55
54
52
80
96
95
8
40
32
48
48
48
47
67
71
67
7
27
11
57
51
51
53
62
60
54
23
20
172
23
21
39
59
58
55
51
41
0
20
25
21
0
158
59
53
50
50
Figure 5.6(d): Orientation preference (in degrees) for a bunch of neurons (Plus/Minus)
74
Figure 5.6(e): Scatter Plot for Gaussian simulation
Figure 5.6(f): Scatter Plot for Plus/Minus simulation
The question that one might ask is why does LISSOM exhibit such type of behaviour.
This can probably be explained by considering figure 5.7, which depicts the left-eye and
right-eye receptive field of a hypothetical neuron. Let us assume that each RF encloses
100 retinal receptors, such that our neuron has 100 connections to each retina. Each
connection has a weight associated with it. Let us also assume that the input pattern
covers 40 receptors in each eye, namely, RL1 to RL40 in the left retina and RR1 to RR40 in
the right retina. In this example, large patterns have been purposefully used to stress on
how phase differences might develop. During this particular input presentation, the
weights associated with these receptors will be affected to a greater extent. Since
75
RL1…RL40 do not correspond to RR1…RR40, and because of the vertical orientation, a
phase difference creeps in between the left-eye and right-eye RF. It can intuitively be
deduced that for horizontal orientations, there cannot be any such phase differences,
unless vertical retinal disparity is also present. However, if small horizontally-oriented
patterns are used, we would most probably observe a few cases of position disparity
(i)Left Retina
(ii)Right Retina
Figure 5.7: Vertically-oriented patterns
5.4 VALIDATION AGAINST BIOLOGICAL DATA
The main topics of discussion in this chapter have been about the distribution of phase
disparity preferences among cortical neurons and the relation between phase disparity
preference and orientation preference. The LISSOM-based model developed a
topographic map in which an overwhelming majority of neurons prefer phase disparities
in the region of 0°, but the map also included patches of neurons preferring larger
magnitudes of phase disparity. It has been seen that these neurons tend to prefer
orientations that have a significant vertical component. These two findings need to be
validated against biological data to assess the plausibility of the model.
5.4.1 DISTRIBUTION OF PHASE DISPARITIES
The work done by Anzai et al (1999a) on neural mechanisms involved in the encoding
of binocular disparity provides a good comparison platform. Anzai and colleagues
investigated the role of position and phase in the encoding of disparity in cats. They
inspected 97 simple cells in 14 adult cats and compiled a frequency distribution for the
observed phase disparities. They found out that phase disparities are distributed around
zero, indicating that cells with similar RF profiles are most numerous (Anzai et al,
1999a). It was also observed that the disparities were mostly limited between -90° and
90°, although some disparities beyond that range were also recorded (Anzai et al,
1999a).
76
Figure 5.8: Histogram of phase disparity compiled by Anzai et al from results obtained
in cells from cats (reprinted from [3])
5.4.2 DISPARITY AND ORIENTATION PREFERENCE
Studies have shown that RF profiles for the left and right eyes are more or less the same
for cells tuned to horizontal orientations, whereas those for cells tuned to vertical
orientations show a certain degree of dissimilarity (DeAngelis et al, 1991, 1995;
Ohzawa et al. 1996). The study by Anzai et al also confirmed this. This is because the
eyes are displaced laterally, and due to binocular parallax, a larger range of binocular
disparities is along horizontal compared to vertical directions; consequently, phase
disparity is expected to be larger for cells preferring vertical orientations (Anzai et al,
1999a).
5.5 SUMMARY
The LISSOM-based experiments have shown that disparity-selectivity develop as a
result of input-driven self-organization. It was found that cortical neurons develop left
and right-eye RF profiles that differ in phase when trained with inputs presented at noncorresponding points on the retinas. Most of the neurons prefer phase disparities in the
region of zero, as has been shown to be the case in biology. Moreover, the magnitude of
the phase disparities has been observed to be below 90° in experiments with reasonable
amount of retinal disparity (2.0 retinal units). This corroborates with work done by
Blake and Wilson (1991), and Marr and Poggio (1979), who remarked that phase
disparity must be limited to 90° “in order for band-pass filters to unambiguously encode
binocular disparity” (Anzai et al, 1999a). This is also confirmed by Anzai and
colleagues, although phase disparities larger than 90° were also recorded during their
77
study on simple cells in the cat’s striate cortex. Since the self-organizing process
depends a lot on the input type, it would be interesting to investigate the effects of input
patterns other than the elongated Gaussians that have been used in this project. The
Gaussian and Plus/Minus experiments yielded disparity maps that were not a great deal
different from each other despite the fact that the RF structures in either case were quite
dissimilar.
The other notable observation concerns the relationship between phase disparities and
orientation preference. The simulation results have shown that in general, neurons with
dissimilar left and right-eye RF profiles tend to prefer vertical orientations. This is
backed by the biological recordings of Anzai et al (1999a) and also by the observations
made by Ts’o et al (2001) during their impressive study on region V2 of monkeys. The
LISSOM results tend to suggest that regions with a preferred orientation in the vicinity
90° contain subcompartments that are selective for relatively high phase disparities,
while regions that contain neurons preferring orientations with a significant component
might be containing substructures with preferred phase disparities around zero.
78
CHAPTER 6
CONCLUSION AND FUTURE WORK
6.1 CONCLUSION
The topographic representation of features in the primary visual cortex has been the
focus of many studies; it is believed that an understanding of the neural mechanisms
involved in topography can provide the foundations to formulate general theories about
learning, memory and knowledge representation in the brain (Swindale, 1996). The
ordered arrangement of neurons in V1 is a consequence of a self-organizing process that
is believed to take place in both pre-natal and post-natal stages. Computational
modelling is increasingly being used to simulate this process in an attempt to help
neurobiologists in their quest for answers. Many models have successfully simulated the
self-organizing process for features like orientation and ocular dominance, and results
have been in phase with experimental data. But little or no work has been done to
investigate binocular disparity, believed to be a major visual cue for the perception of
depth. This study is the first of its kind to investigate disparity selectivity in LISSOM,
and is one among few others that have used some self-organizing algorithm to
investigate this feature. The main aim of this project was to investigate the input-driven
self-organizing process for disparity selectivity in LISSOM. Simulation results with
simple elongated Gaussians as input have shown that cortical neurons develop left and
right-eye receptive fields that differ in phase. It was found that an overwhelming
majority of the neurons preferred phase disparities close to zero, with the rest having a
preferred disparity of less than 40° for experiments with relatively small retinal
disparities. The type of input used for training seems to affect the overall disparity map,
but not by much; when Gaussians brighter than the background were used as inputs,
almost all of the neurons develop phase disparities of magnitude less than 30°, while in
the case of random bright and dark Gaussian input patterns, the threshold is around 40°
for the vast majority. An interesting observation in either case concerns the relationship
between disparity selectivity and orientation preference. The results show that neurons
that prefer vertical or near-vertical orientations tend to develop relatively large phase
differences between their monocular receptive fields, while neurons that prefer
orientations around 0° tend to have similar monocular RFs. . This suggests that cortical
regions grouped by orientation preferences might be subdivided into compartments that
are in turn organised based on disparity selectivity. But before jumping to conclusions,
more in-depth computational experiments have to be carried out. Several disparityrelated issues could not be investigated due to time constraints, the most important one
probably being the implementation of complex cells. The next section describes some of
79
the key points that need to be investigated to eventually provide a concrete, testable
explanation for the self-organization mechanism of disparity selectivity so as to assist
theoretical neuroscientists in better understanding the functioning of the brain.
6.2 FUTURE WORK
6.2.1 PHASE INVARIANCE
First and foremost, the phase invariance issue has to be resolved. Although the ODF
model simulates complex cells quite nicely and has proved to produce biologically
plausible results, it lacks developmental capabilities, i.e. it is difficult to integrate it
within a self-organizing model. It is a very specific model that follows certain fixed
rules. There is a need for a more flexible approach that can be integrated within the selforganizing framework of LISSOM. Because of lack of time, such a model could not be
implemented, but a potential approach is proposed in this section to serve as a guide in
extending the work done on the phase invariance issue in LISSOM. It is based on the
temporal trace rule developed by Foldiak (1991) and is largely inspired from a selforganizing model proposed by Sullivan and R. de Sa (2004).
The temporal trace rule is a modified Hebbian rule in which weight adaptation is based
on the presynaptic activity(x) and to a trace, or average value, of the postsynaptic
activity (ỹ). A trace is a running average of the activation of a neuron, such that activity
of the unit at a particular moment influences learning at a later moment (Foldiak, 1991).
The main idea behind this rule is that input stimuli that are close together on a temporal
scale are likely to be generated by the same object (Sullivan and R. de Sa, 2004). The
rule is characterized by these equations, as formulated by Foldiak,
where
ỹ(t) is the trace value for a complex cell
ỹ(t-1) is the previous trace value, i.e. the trace value at the previous time step
y(t) is the instantaneous activation based on visual stimuli (using the dot-product rule)
δ is a decay term.
The model by Sullivan and R. de Sa comprises three learning rules, namely Hebbian
Learning, the temporal trace rule and SOM. It consists of a simple cell layer and a
complex cell layer. The simple cell layer consists of identical groups of neurons having
80
similar orientation-preferences while the complex cell layer is initially unorganized. So
the basic assumption is that self-organization has already taken place among the simple
cells before they contribute towards the learning process of the complex cells. This is
not an unrealistic assumption since, as the authors point out, work done by Albus and
Wolf (1984) indicated that simple cells in cats are orientation selective before the input
reaches the complex cells in layers 2/3 of the striate cortex. Another assumption made
by Sullivan and R. de Sa is that the complex cells all respond to the same receptive
field, which is very unrealistic, as humbly acknowledged by the authors.
For the proposed model, the first assumption will be maintained but the second one will
be dropped. Instead of a fully-connected network between the simple cell layer and the
complex cell layer, each unit in the output layer will have a connection field enclosing a
suitably-sized region in the simple cell layer. So basically, if only one eye is considered,
there will be an input sheet, the customary LGN ON and OFF sheets, and a couple of
other sheets corresponding to the simple and complex layers. This is shown in figure
6.1.
Figure 6.1: Proposed model for phase-invariant response
There will be two learning phases, the first one directed towards the topographic
organization of the units in the Simple sheet, and the second one for the learning process
of the complex cells. During the first phase, the connections between the Simple and
81
Complex sheets would be inactive. One possible type of input for this stage could be
Plus/Minus elongated Gaussians to allow the development of different kinds of RF
profiles in the Simple layer. During the second stage, learning should be switched off
(Topographica provides this option) for the afferent connections to the Simple layer.
The connections from this layer to the Complex layer can then be activated. The inputs
for this phase of training could be in the form of a series of activity wave line stimuli
that are swept across the retina in discretized time steps (Sullivan and R. de Sa, 2004;
Foldiak, 1991). The relative brightness of the line with respect to the background, and
its orientation, can be randomized for each sweep. This kind of activity can be a model
of the pre-natal retinal waves (Sullivan and R. de Sa, 2004; Foldiak, 1991). By
sweeping the line stimulus across the eye, simple units of the appropriate orientation
and phase-preference will be activated in different positions at different moments of
time (Foldiak, 1991). The activation of these simple units would be the input to the
complex cell layer. If activation of these simple units excites a complex cell, then the
trace of this cell is enhanced for a certain period of time (preferably the number of time
steps it would take to traverse the receptive of the complex cell, although this is not a
trivial matter since the receptive of a cortical neuron is not explicitly defined in
LISSOM when multiple sheet layers are used). All the connections from the simple
units that get activated during that time period get strengthened according to the trace
rule (Foldiak, 1991). Only those simple cells that have a preferred orientation similar to
the orientation of the bar stimulus would be activated, thus making the complex cell
strongly selective for that orientation. Note that phase independence would also
potentially develop after training since the brightness of the bar stimuli relative to the
background is randomized for each sweep. So, for the region of the retina that
corresponds to the receptive field of a particular complex cell, an optimally-oriented bar
would in theory excite that cell irrespective of its brightness and position, after many
permutations of the input stimuli have been presented. The presence of lateral
connections in the complex cell layer would possibly lead to the formation of an
ordered map for orientation, just like in the current simple-cell versions of LISSOM.
The proposed model is just a rough guide to what might be done to get phase invariance
in LISSOM. Its implementation might necessitate a look at some other intricacies that
have been overlooked. It is somewhat different from the model proposed by Sullivan
and R. de Sa. The latter mention that their model captures phase invariance, but refer to
this property as the response of a complex cell to an optimally-oriented stimulus
anywhere within the receptive field of the cell. This is contradictory since it points
towards position invariant response rather than phase invariant response. The proposed
model tries to deal both with position invariance and phase invariance. If the
82
implementation of the one-eye model does yield reliable results, it can be extended to a
two-eye model and disparity-selectivity can be investigated.
6.2.2 DISPARITY SELECTIVITY AND OCULAR DOMINANCE
Many studies have focused on both disparity selectivity and ocular dominance, but it is
still unclear if there is some kind of relationship between these two features. Certain
studies have shown that manipulations with OD columns also affect stereopsis, and that
these two features appear and mature with similar time-courses (Gonzales and Perez,
1998). Gonzales and colleagues suggest that “binocularity may not be an obligate
feature of a cell to be involved in the stereoscopic process” (Gonzales and Perez, 1998).
Some studies have shown that disparity sensitivity is strongly associated with binocular
neurons, as one would expect, but other investigations have surprisingly indicated that
disparity-selective cells are strongly dominated by one eye (Gonzales and Perez, 1998).
This might all be tied up to the type of cell and influence of excitatory and inhibitory
connections from each eye. It would be worthwhile to investigate the relationship, if
any, between disparity selectivity and ocular dominance in LISSOM to shed some light
into this issue. The script for the self-organizing process leading to OD, and the OD
map-measuring functionality have been implemented in Topographica during the
course of this project. Unfortunately, proper experiments could not be performed
because one particular functionality in Topographica, namely Joint Normalization, was
not working properly. As its name suggests, it takes all the afferent connections into
consideration for normalization, instead of independently normalizing each connection.
Joint Normalization is important while investigating ocular dominance since input
patterns differ in brightness level on each retina, and therefore there is a need to reflect
these differences among the connection weights during learning.
6.2.3 VERTICAL DISPARITY
Horizontal disparity represents the major visual cue for stereopsis, but it is not enough
to compute stereo depth on its own (Gonzalez and Perez, 1998). Certain reports have
suggested that vertical disparity might play a role in calibrating horizontal disparities in
the depth perception process while other studies deny this (Gonzalez and Perez, 1998).
Once again computational modeling can help in disambiguate this matter. It is
straightforward to include vertical retinal disparity in the current scripts, but caution
must be observed while setting a value to it, since physiological studies suggest that
vertical disparities are very small as compared to horizontal disparities
83
6.2.4 PRENATAL AND POSTNATAL SELF-ORGANIZATION
Very little is known about the effects of prenatal activity on the development of
disparity selectivity in V1. Prior work in this area is almost non-existent. However,
Berns et al (1993) attempted to probe into this and their experiment yielded some
interesting results. They used a model consisting of 2 retinas and a cortical layer fully
connected with synaptic weights that used Hebbian adaptation. The model also included
lateral connections in the cortical layer. They found out that with no correlations present
between the eyes, the model developed only monocular cells, but with correlation, the
cortical neurons formed were completely binocular. But with an initial phase of sameeye correlations and a second phase with both same-eye and between-eye correlations, a
mixture of disparity-selective monocular and binocular cells were observed to form
(Berns et al, 1993). Although the model used is not a robust representation of biological
systems, the results tend to indicate that disparity selectivity is very much influenced by
both prenatal and postnatal activities. An extension to the work done in this project
could be the investigation of both spontaneous and visually-evoked activity in the selforganizing process. Spontaneous activity can be simulated using noisy disk model of
retinal waves and postnatal training can be achieved using stereo images. The procedure
would be similar to the one that has already been used in the study of influence of
genetic and environmental factors on the development of orientation maps in V1 using
LISSOM. It would be interesting to observe the impact of stereo images during training
after the noisy disk phase, especially since use of stereo images alone did not yield
conclusive results during this study
84
BIBLIOGRAPHY
[1].
Albus, K., and Wolf, W. (1984). Early postnatal development of neuronal function in
the kitten’s visual cortex: A laminar analysis. The Journal of Physiology, 348:153–185.
[2].
Anzai, A., Ohzawa, I., Freeman, R.D., 1997. Neural mechanisms underlying binocular
fusion and stereopsis: position v/s phase. Proc. Natl. Acad. Sci. USA 94, 5438–5443.
[3].
Anzai, A., Ohzawa, I., and Freeman, R. D. Neural mechanisms for encoding binocular
disparity: position versus phase. J. Neurophysiol. 82: 874–890, 1999a.
[4].
Barlow, H.B., Blakemore, C., Pettigrew, J.D., 1967. The neural mechanisms of
binocular depth discrimination. J. Physiol. 193, 327–342.
[5].
Berns G.S., Dayan P., and Sejnowski T.J. A correlational model for the development of
disparity selectivity in visual cortex that depends on prenatal and postnatal phases. Proc
Natl Acad Sci U S A. 1993 Sep 1;90(17):8277-81
[6].
Bishop,P.O (1989) Vertical disparity, egocentric distance and stereoscopic depth
constancy: a new interpretation. Proc. R. Soc. London Ser. B 237,445-469
[7].
Blake, R. and Wilson, H. R. Neural models of stereoscopic vision. Trends Neurosci. 14:
445–452, 1991.
[8].
Blakemore, C. (1970) The representation of three-dimensional visual space in the cat’s
striate cortex. J. Physiol. (Lond) 209, 155–178
[9].
Blasdel, G. G., and Salama, G. (1986). Voltage-sensitive dyes reveal a modular
organization in monkey striate cortex. Nature, 321:579–585.
[10].
Cowey, A. and Ellis, C.M. (1967) Visual acuity of rhesus and squirrel monkeys. J.
Comp. Physiol. Psychol. 64, 80-84
[11].
DeAngelis, G. C., Ohzawa, I., and Freeman, R. D. Depth is encoded in thevisual cortex
by a specialized receptive field structure. Nature 352: 156–159, 1991.
[12].
DeAngelis, G. C., Ohzawa, I., and Freeman, R. D. Neuronal mechanisms underlying
stereopsis: how do simple cells in the visual cortex encode binocular disparity?
Perception 24: 3–31, 1995.
85
[13].
DeAngelis, G.C., Newsome, W.T., 1999. Organization of disparity-selective neurons in
macaque area MT. J. Neurosci.19, 1398–1415.
[14].
DeAngelis, G.C., Seeing in three dimensions: the neurophysiology of stereopsis. Trends
in Cognitive Sciences – Vol. 4, No. 3, March 2000
[15].
Devalois, R. and Jacobs, G. H. (1968) Primate vision color, Science 162, 533-540
[16].
Devalois, R. L. and Devalois, K. K. Spatial Vision. New York: Oxford,1988.
[17].
Farrer, D.N. and Graham, E.S (1967) Visual acuity in monkeys. A monocular and
binocular subjective technique.Vision Res. 7, 743-747
[18].
Fischer B and Krueger J. Disparity tuning and binocularity of single neurons in cat
visual cortex. Exp Brain Res 35: 1–8, 1979.
[19].
Fischer B and Poggio GF. Depth sensitivity of binocular cortical neurons of behaving
monkeys. Proc R Soc Lond B Biol Sci 204: 409–414, 1979.
[20].
Fleet, D. J., Wagner, H., and Heeger, D. J. Neural encoding of binocular disparity:
energy models, position shifts and phase shifts. Vision Res. 36: 1839–1857, 1996.
[21].
Foldiak, P. (1991). Learning invariance from transformation sequences. Neural
Computation, 3:194–200
[22].
Freeman, R. D. and Ohzawa, I. On the neurophysiological organization of binocular
vision. Vision Res. 30: 1661–1676, 1990.
[23].
Gonzalez, F., Krause, F. ,Perez, R.,Alonso, J.M.and Acuna, C. (1993a) Binocular
matching in monkey visual cortex: single cell responses to correlated and uncorrelated
dynamic random dot stereograms. Neuroscience 52, 933-939
[24].
Gonzales, F. and Perez R. (1998) Neural mechanisms underlying stereoscopic vision
Progress in Neurobiology 55, 191-224
[25].
Gonzalez F, Perez R, Justo MS, and Ulibarrena C. Binocular interaction and sensitivity
to horizontal disparity in visual cortex in the awake monkey. Int J Neurosci 107: 147–
160, 2001.
[26].
http://www.nei.nih.gov/photo/eyean/ (first visited 13/08/06)
86
[27].
Harweth, R.S., Smith, E.T. and Siderov, J. (1995) Behavioral studies of local stereopsis
and disparity vergence in monkeys, Vision Res. 35, 1755-1770
[28].
Hubel, D.H., Wiesel, T.N., 1962. Receptive fields binocular interaction and functional
architecture in the cat’s visual cortex
[29].
Hubel D.H., Wiesel T.N. (1977) Functional architecture of macaque monkey visual
cortex. Proc R Soc Lond B 198:1-59
[30].
Hubel, D., Eye, Brain, and Vision (Scientific American Library Series, 1995)
[31].
Hubener m., Shoham D., Grinvald A, Bonhoeffer T (1997) Spatial relationships among
three columnar systems in cat area 17. J Neurosci 17, 9270-9284
[32].
Joshua, D.E. and Bishop, P.O (1970) Binocular single vision and depth discrimination.
Receptive field disparities for central peripheral vision and binocular interaction on
peripheral single units in cat striate cortex. Exp. Brain Res. 10, 389-416
[33].
Julesz, B (1971) Foundations of Cyclopean Perception, University of Chicago Press:
Chicago
[34].
Kohonen, T. (1982b). Self-organized formation of topologically correct feature maps.
Biological Cybernetics, 43:59–69.
[35].
LeVay, S. and Voigt, T. (1988) Ocular Dominance and disparity coding in cat visual
cortex. Visual Neurosci. 1, 395- 414
[36].
Levine M.W. and Shefner, J.M. (1991). Fundamentals of sensation and perception, 2nd
ed. Pacific Grove, CA: Brooks/Cole.
[37].
Marr, D. and Poggio, T. A computational theory of human stereo vision. Proc. R. Soc.
Lond. B Biol. Sci . 204: 301–328, 1979.
[38].
Maske, R., Yamane, S., and Bishop, P. O. Binocular simple cells for local stereopsis:
comparison of receptive field organizations for the two eyes.Vision Res. 24: 1921–1929,
1984.
[39].
Miikkulainen, R., Bednar, J. A., Choe, Y., and Sirosh, J. (1997). Self-organization,
plasticity, and low-level visual phenomena in a laterally connected map model of the
primary visual cortex. In Goldstone, R. L., Schyns, P. G., and Medin, D. L., editors,
Perceptual Learning, volume 36 of Psychology of Learning and Motivation, 257–308.
San Diego, CA: Academic Press.
87
[40].
Miikkulainen, R., Bednar, J.A. , Chloe Y., Shirosh, J. Computational Maps in the
Visual Cortex (New York: Springer 2005)
[41].
Nikara, T., Bishop, P. O., and Pettigrew, J. D. Analysis of retinal correspondence by
studying receptive fields of binocular single units in cat striate cortex. Exp. Brain Res.
6: 353–372, 1968
[42].
Nomura, M., Matsumoto, G., and Fujiwara, S. A binocular model for the simple cell.
Biol. Cybern. 63: 237–242, 1990.
[43].
Ohzawa, I., Freeman, R.D., 1986a. The binocular organization of complex cells in the
cat’s visual cortex.J. Neurophysiol. 56, 243–259.
[44].
Ohzawa, I., Freeman, R.D., 1986b. The binocular organization of simple cells in the
cat’s visual cortex.J. Neurophysiol. 56, 221–24
[45].
Ohzawa, I., DeAngelis, G.C., Freeman, R.D., 1990. Stereoscopic depth discrimination
in the visual cortex: neurons ideally suited as disparity detectors. Science 249, 1037–
1041.
[46].
Ohzawa, I., DeAngelis, G. C., and Freeman, R. D. Encoding of binocular disparity by
simple cells in the cat’s visual cortex. J. Neurophysiol. 75:1779–1805, 1996.
[47].
Ohzawa, I., DeAngelis, G. C., and Freeman, R. D. Encoding of binocular disparity by
complex cells in the cat’s visual cortex. J. Neurophysiol. 77:2879–2909, 1997.
[48].
Poggio GF and Fischer B.(1977) Binocular interaction and depth sensitivity of striate
and prestriate cortex of behaving rhesus monkey. J Neurophysiol 40:1392–1405
[49].
Poggio, G.F. and Talbot, W.H. (1981) Mechanisms of static and dynamic stereopsis in
foveal cortex of the rhesus monkey. J Physiol. Lond. 315, 469- 492
[50].
Poggio, G.F., Poggio, T., 1984. The analysis of stereopsis. Ann. Rev. Neurosci. 7, 379–
412.
[51].
Poggio, G.F., Motter, B.C., Squatrito, S., Trotter, Y., 1985. Responses of neurons in
visual cortex (V1 and V2) of the alert macaque to dynamic random-dot stereograms.
Vision Res. 25, 397–406.
[52].
Poggio GF, Gonzalez F, and Krause F. (1988) Stereoscopic mechanisms in monkey
visual cortex: binocular correlation and disparity selectivity. J Neurosci 8: 4531-4550
88
[53].
Prince SJ, Pointon AD, Cumming BG, and Parker AJ. (2002b) Quantitative analysis of
the responses of V1 neurons to horizontal disparity in dynamic random-dot
stereograms. J Neurophysiol 87: 191–208.
[54].
Qian, N., (1994). Computing stereo disparity and motion with known binocular cell
properties. Neural Comp. 6,390–404.
[55].
Qian, N., (1997) Binocular disparity and the perception of depth. Neuron. 18, 359–368.
[56].
Qian, N. and Zhu, Y. (1997) Physiological computation of binocular disparity. Vision
Res. 37: 1811–1827.
[57].
Read, J.C.A. 2005. Early computational processing in binocular vision and depth
perception. Progress in Biophysics and Molecular Biology 87 (2005) 77–108
[58].
Read, J.C.A., Parker, A.J., Cumming, B.G., 2002. A simple model accounts for the
reduced response of disparity-tuned V1 neurons to anti-correlated images. Vis.
Neurosci. 19, 735–753.
[59].
Schmuel A, Grinvald A (1996) Functional organization for direction of motion and its
relationship to orientation maps in area 18. J Neurosci 16, 6945-6964
[60].
Skottun, B.C., DeValois, R.L., Grosof, D.H., Movshon, J.A., Albrecht,D.G., and Bonds,
A.B. (1991). Classifying simple and complex cells on the basis of reponse modulation.
Vision Res. 31, 1079–1086.
[61].
Sirosh, J., and Miikkulainen, R. (1993). How lateral interaction develops in a selforganizing feature map. In Proceedings of the IEEE International Conference on
Neural Networks (San Francisco, CA), 1360–1365. Piscataway, NJ: IEEE
[62].
Sullivan, T.J. and R. de Sa, V. (2004) A temporal trace and SOM-based model of
complex cell development, Neurocomputing, 58-60, 827-833
[63].
Swindale N.V. (2000) The development of topography in the visual cortex: a review of
models. Network: Computation in Neural Systems 7, 161-247
[64].
Swindale N.V. (2000) How Many Maps are there in Visual Cortex? Cerebral Cortex,
Vol. 10, No. 7, 633-643
[65].
Tootell, R.B.H., and Hamilton, S.L. (1989). Functional anatomy of the second visual
area (V2) in the Macaque. Journal of Neuroscience, 9, 2620-2644
89
[66].
Ts’o, D.Y., Roe, A.W., and Gilbert, C.D. (2001). A hierarchy of the functional
organization for color, form and disparity in primate visual area V2. Vision Research,
41, 1333-1349
[67].
Von Der Heydt, R., Adorjani, C. S., Hanny, P., and Baumgartner, G. Disparity
sensitivity and receptive field incongruity of units in the cat striate cortex. Exp. Brain
Res. 31: 523–545, 1978.
[68].
Von der Malsburg, C. (1973). Self-organization of orientation-sensitive cells in the
striate cortex. Kybernetik, 15:85–100. Reprinted in Anderson and Rosenfeld (1988),
212–227.
[69].
Wiemer, J., Burwick,T., von Seelen, W. (2000) Self-organizing maps for feature
representation based on natural binocular stimuli. Biol. Cybern. 82, 97-110 (2000)
[70].
Weliky M, Bosking WH, Fitzpatrick D (1996) A systematic map of direction preference
in primary visual cortex. Nature 379, 725-728
[71].
Zhu, Y. and Qian, N. Binocular receptive field models, disparity tuning, and
characteristic disparity. Neural Comput. 8: 1611–1641, 1996.
90