Download HMMs for gene predictions.

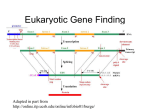
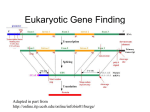
Gene prediction and HMM
Computational Genomics 2005/6
Lecture 9b
Slides taken (and rapidly mixed) from William Stafford Noble,
Larry Hunter, and Eyal Pribman. Partially modified by Benny
Chor.
Annotation of
Genomic Sequence
Given the sequence of an organism’s genome, we
would like to be able to identify:
–
–
–
–
–
Genes
Exon boundaries & splice sites
primary goals
Beginning and end of translation
Alternative splicings
secondary goals
Regulatory elements (e.g. promoters)
The only certain way to do this is experimentally,
but it is time consuming and expensive. Computational
methods can achieve reasonable accuracy quickly, and
help direct experimental approaches.
Prokaryotic Gene Structure
Promoter
CDS
Terminator
Genomic DNA
transcription
mRNA
 Most
bacterial promoters contain the Shine-Delgarno signal, at
about -10 that has the consensus sequence: 5'-TATAAT-3'.
 The terminator: a signal at the end of the coding sequence that
terminates the transcription of RNA
 The coding sequence is composed of nucleotide triplets. Each
triplet codes for an amino acid. The AAs are the building blocks
of proteins.
Pieces of a (Eukaryotic) Gene
(on the genome)
~ 1-100 Mbp
5’
3’
3’
5’
~ 1-1000 kbp
5’ …
…
3’
… 3’
…
5’
exons (cds & utr) / introns
(~ 102-103 bp)
(~ 102-105 bp)
promoter (~103 bp)
enhancers (~101-102 bp)
Polyadenylation
site
other regulatory sequences
(~ 101-102 bp)
What is it about genes that we
can measure (and model)?
• Most of our knowledge is biased towards
protein-coding characteristics
– ORF (Open Reading Frame): a sequence defined by inframe AUG and stop codon, which in turn defines a
putative amino acid sequence.
– Codon Usage: most frequently measured by CAI (Codon
Adaptation Index)
• Other phenomena
– Nucleotide frequencies and correlations:
• value and structure
– Functional sites:
• splice sites, promoters, UTRs, polyadenylation sites
A simple measure: ORF length Comparison of
Annotation and Spurious ORFs in S. cerevisiae
Basrai MA, Hieter P, and Boeke J Genome Research 1997 7:768-771
Codon Adaptation Index (CAI)
 f codon
i
CAI   
i  codons  f  codoni 
max




• Parameters are empirically determined by
examining a “large” set of example genes
• This is not perfect
– Genes sometimes have unusual codons for a reason
– The predictive power is dependent on length of
sequence
Splice signals (mice): GT , AG
General Things to Remember about
(Protein-coding) Gene Prediction Software
• It is, in general, organism-specific
• It works best on genes that are reasonably similar
to something seen previously
• It finds protein coding regions far better than noncoding regions
• In the absence of external (direct) information,
alternative forms will not be identified
• It is imperfect! (It’s biology, after all…)
Simple HMM : Prokaryotes
0
0
0
 0
0.5 0.998 0.002 0


0.5 0.001 0.996 0


0
0
.
001
0
.
002
0


0.28
0.22
H 
0.25

0.25
0.32
0.18 

0.18 

0.32
xm(i) = probability of being in state m at position i;
H(m,yi) = probability of emitting character yi in state m;
mk = probability of transition from state k to m.
Outline: Rest of Lecture
•
•
•
•
•
Eukaryotic gene structure
Modeling gene structure
Using the model to make predictions
Improving the model topology
Modeling fixed-length signals
A eukaryotic gene
• This is the human p53 tumor suppressor
gene on chromosome 17.
• Genscan is one of the most popular gene
prediction algorithms.
A eukaryotic gene
Introns
Final exon
3’ untranslated
region
Initial exon
Internal exons
This particular gene lies on the reverse strand.
An Intron
revcomp(CT)=AG
GT: signals start of intron
AG: signals end of intron
3’ splice site
revcomp(AC)=GT
5’ splice site
Signals vs contents
• In gene finding, a small pattern within the
genomic DNA is referred to as a signal, whereas
a region of genomic DNA is a content.
• Examples of signals: splice sites, starts and
ends of transcription or translation, branch
points, transcription factor binding sites
• Examples of contents: exons, introns, UTRs,
promoter regions
Prior knowledge
• We want to build a probabilistic model of a
gene that incorporates our prior knowledge.
• E.g., the translated region must have a
length that is a multiple of 3.
Prior knowledge
• The translated region must have a length that is
a multiple of 3.
• Some codons are more common than others.
• Exons are usually shorter than introns.
• The translated region begins with a start signal
and ends with a stop codon.
• 5’ splice sites (exon to intron) are usually GT;
• 3’ splice sites (intron to exon) are usually AG.
• The distribution of nucleotides and dinucleotides
is usually different in introns and exons.
A simple gene model
Intergenic
Intergenic
Start
Intergenic
Transcription
start
Gene
Intergenic
Transcription
stop
End
A probabilistic gene model
Pr(TACAGTAGATATGA) = 0.0001
Pr(AACAGT) = 0.001
Pr(AACAGTAC) = 0.002
…
Intergenic
Intergenic
0.67
Start
0.33
0.25
Transcription
start
1.00
Gene
Transcription
stop
Intergenic
Every box stores transition probabilities for outgoing arrows.
Every arrow stores emission probabilities for emitted nucleotides.
Intergenic
0.75
End
Parse
S = ACTGACTACTACGACTACGATCTACTACGGGCGCGACCTATGCG
P = IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIGGGGG
TATGTTTTGAACTGACTATGCGATCTACGACTCGACTAGCTAC
GGGGGGGGGGIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
• For a given sequence, a parse is an assignment of gene
structure to that sequence.
• In a parse, every base is labeled, corresponding to the
content it (is predicted to) belongs to.
• In our simple model, the parse contains only “I”
(intergenic) and “G” (gene).
• A more complete model would contain, e.g., “-” for
intergenic, “E” for exon and “I” for intron.
The probability of a parse
Pr(ATGCGTATGTTTTGA) =
0.00000000142
Pr(ACTGACTACTACGACTACGAT
CTACTACGGGCGCGACCT) =
0.0000543
Pr(ACTGACTATGCGATCTACGAC
TCGACTAGCTAC) = 0.0000789
Intergenic
Intergenic
0.67
Start
0.33
0.25
Transcription
start
1.00
Gene
Transcription
stop
Intergenic
0.75
End
Intergenic
S = ACTGACTACTACGACTACGATCTACTACGGGCGCGACCTATGCGTATGTTTTGAACTGACTATGCGATCTACGACTCGACTAGCTAC
P = IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIGGGGGGGGGGGGGGGIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
Pr(parse P| sequence S, model M)
= 0.67  0.0000543  1.00  0.00000000142  0.75 x 0.0000789
= 3.057  10-18
Finding the best parse
• For a given sequence
S, the model M
assigns a probability
Pr(P|S,M) to every
parse P.
P*  arg max Pr p S , M
p
• We want to find the
parse P* that receives
the highest
probability.


Beyond Simplest Model
• Improving the gene model topology
• Fixed-length signals
– PSSMs
– Dependencies between positions
• Variable-length contents
– Using HMMs
– Semi-Markov models
• Parsing algorithms
– Viterbi
– Posterior decoding
• Including other types of data
– Expressed sequence tags
– Orthology
Improved model topology
Intergenic 2
Intergenic 1
Transcription
Start
start
Intergenic 4
Gene
Transcription
stop
Intergenic 3
• Draw a model that includes introns
End
Improved model topology
Start
Transcription
start
5’ splice
site
3’ splice
site
Transcription
stop
End
Improved model topology
Start
Transcription
start
5’ splice
site
4 intergenics
1 intron
4 exons
3’ splice
site
Transcription
stop
End
Improved model topology
Start
Transcription
start
Initial exon
Single exon
Internal exon
5’ splice
site
Intron
3’ splice
site
Final exon
Transcription
stop
End
Modeling the 5’ splice site
5’ splice
site
GT
Intron
3’ splice
site
• Most introns begin with the letters “GT.”
• We can add this signal to the model.
Modeling the 5’ splice site
5’ splice
site
G
Pr(A)=0
Pr(C)=0
Pr(G)=1
Pr(T)=0
T
Intron
3’ splice
site
Pr(A)=0
Pr(C)=0
Pr(G)=0
Pr(T)=1
• Most introns begin with the letters “GT.”
• We can add this signal to the model.
• Indeed, we can model each nucleotide
with its own arrow.
Modeling the 5’ splice site
5’ splice
site
G
Pr(A)=0.01
Pr(C)=0.01
Pr(G)=0.97
Pr(T)=0.01
T
Intron
3’ splice
site
Pr(A)=0.01
Pr(C)=0.01
Pr(G)=0.01
Pr(T)=0.97
• Like most biological phenomenon, the
splice site signal admits exceptions.
• The resulting model of the 5’ splice site is
a length-2 PSSM.
Real splice sites
• Real splice sites show some conservation at
positions beyond the first two.
• We can add additional arrows to model these
states.
weblogo.berkeley.edu
Modeling the 5’ splice site
5’ splice
site
Intron
3’ splice
site
Adding signals
Start
Transcription
start
Initial exon
Single exon
Internal exon
5’ splice
site
Intron
3’ splice
site
Final exon
Transcription
stop
Red ellipses correspond
to signal models like this:
End
Positional Independence
Pr(“ACTT”|M)
= Pr(“A” at position 1 and “C” at position 2 and “T”
at position 3 and “T” at position 4|M)
= Pr(“A” at position 1|M)  Pr(“C” at position 2|M) 
Pr(“T” at position 3|M)  Pr(“T” at position 4|M)
• In general, probabilities of independent events
get multiplied.
• A PSSM assumes independence among
nucleotides at different positions.
Positional dependence
• In this data, every
time a “G” appears in
position 1, an “A”
appears in position 3.
• Conversely, an “A” in
position 1 always
occurs with a “T” in
position 3.
ACTG
ACTT
GCAC
ACTT
ACTA
GCAT
ACTA
ACTT
nth-order PSSM
• Normally, PSSM entry (i,j)
gives the score for
observing the ith letter in
position j.
• In an nth-order PSSM,
each score is conditioned
on the preceding letters in
the sequence.
• The entries A|A, C|A, G|A
and T|A should sum to 1.
1
2
3
4
A|A 0.25 0.45 0.12 0.21
A|C 0.29 0.20 0.24 0.15
A|G 0.33 0.13 0.41 0.33
A|T 0.13 0.22 0.23 0.31
C|A 0.34 0.35 0.09 0.10
…
T|T 0.19 0.24 0.25 0.31
2nd-order PSSM
nth-order PSSM
• Normally, PSSM entry (i,j)
gives the score for
observing the ith letter in
position j.
• In an nth-order PSSM,
each score is conditioned
on the preceding letters in
the sequence.
• How many rows are in a
3rd-order PSSM for
nucleotides? nth-order?
1
2
3
4
A|A 0.25 0.45 0.12 0.21
A|C 0.29 0.20 0.24 0.15
A|G 0.33 0.13 0.41 0.33
The probability of
0.13 0.22
A|T observing
an “A”
in position 3,
0.34 that
0.35
C|A given
we
already observed
… a “C” in position
2.
0.23 0.31
0.09 0.10
T|T 0.19 0.24 0.25 0.31
2nd-order PSSM
Conditional probability
GCG
CAG
CCG
GCG
CCG
CCG
GCG
CCT
CCG
GGG
CGG
GCG
AGG
CAG
CCT
CAT
CCT
GCG
• What is the probability of observing
an “A” at position 2, given that we
observed a “C” at the previous
position?
Conditional probability
GCG
CAG
CCG
GCG
CCG
CCG
GCG
CCT
CCG
GGG
CGG
GCG
AGG
CAG
CCT
CAT
CCT
GCG
• What is the probability of observing an
“A” at position 2, given that we observed
a “C” at the previous position?
• Answer: total number of CA’s divided by
total number of C’s in position 1.
• 3/11 = 27%
• Probability of observing CA = 3/18 =
17%.
Conditional probability
GCG
CAG
CCG
GCG
CCG
CCG
GCG
CCT
CCG
GGG
CGG
GCG
AGG
CAG
CCT
CAT
CCT
GCG
• The conditional probability Pr(x|y) =
Number of occurrences of y:x
Number of occurrences of y:*
where * is any letter.
Conditional probability
GCG
CAG
CCG
GCG
CCG
CCG
GCG
CCT
CCG
GGG
CGG
GCG
AGG
CAG
CCT
CAT
CCT
GCG
• What is the probability of observing
a “G” at position 3, given that we
observed a “C” at the previous
position?
Conditional probability
GCG
CAG
CCG
GCG
CCG
CCG
GCG
CCT
CCG
GGG
CGG
GCG
AGG
CAG
CCT
CAT
CCT
GCG
• What is the probability of observing
a “G” at position 3, given that we
observed a “C” at the previous
position?
• Answer: 9/12 = 75%.
Modeling signals
Start
Transcription
start
Initial exon
Single exon
Internal exon
5’ splice
site
Intron
3’ splice
site
Final exon
Transcription
stop
End
Red ellipses may correspond to nth-order PSSMs.
Modeling variable-length regions
Exon length
Modeling variable-length regions
1. The easy way, using standard HMMs.
2. And why that’s not so great.
How are variable-length insertions
modeled in protein HMMs?
The HMM solution
Fixed-length signals
5’ splice
site
Intron
3’ splice
site
Variable-length content
5’ splice
site
Intron
3’ splice
site
Codons
start
translation
end
translation
Single
exon
2
0
start
0
translation
1
1
Single
exon
2
end
translation
The complete model
Start
Transcription
start
Initial exon
Single exon
Internal exon
5’ splice
site
Intron
3’ splice
site
Final exon
Transcription
stop
End
Red ellipses correspond to nth-order PSSMs.
Every arrow contains an invisible box with a self-loop.
A small problem
0.9
5’ splice
site
0.1
Intron
3’ splice
site
• Say that each blue arrow emits one letter.
• What is the probability that the intron will
be exactly 2 letters long?
• 3 letters long?
• 4 letters long?
A small problem
0.9
5’ splice
site
0.1
Intron
3’ splice
site
• Say that each blue arrow emits one letter.
• What is the probability that the intron will
be exactly 2 letters long? 10%
• 3 letters long? 9%
• 4 letters long? 8.1%
A small problem
HMMs tend to
produce
geometric
distributions
Real contents are not necessarily geometric.
Building an HMM
• Input: annotated gene sequences
• Output: HMM parameters
– Emission distributions within each content
– Length distributions of contents
– Transition distributions between contents
A more realistic (and complex)
HMM model for Gene
Prediction (Genie)
Kulp, D., PhD Thesis, UCSC 2003
Assessing performance:
Sensitivity and Specificity
Testing of predictions is performed on sequences •
where the gene structure is known
Sensitivity is the fraction of known genes (or bases •
or exons) correctly predicted
“Am I finding the things that I’m supposed to find” –
Specificity is the fraction of predicted genes (or •
bases or exons) that correspond to true genes
“What fraction of my predictions are true?” –
In general, increasing one decreases the other •
Graphic View of Specificity and Sensitivity
Sn 
TruePositive
TruePositive

AllTrue
TruePositive  FalseNegative
Sp 
TruePositive
TruePositive

AllPositiv e TruePositive  FalsePosit ive
Quantifying the tradeoff:
Correlation Coefficient


TP TN   FP FN 
CC 
 AN PP  AP PN 
AN  TN  FP; AP  TP  FN ;
PP  TP  FP; PN  TN  FN
Specificity/Sensitivity Tradeoffs
•
1200
random sequence
true sites
1000
800
count
Ideal Distribution of
Scores
600
400
200
0
0
5
10
15
20
25
30
35
40
45
50
score (arb units)
•
1200
random sequence
true sites
1000
count
More Realistically…
800
600
400
200
0
0
10
20
30
score (arb units)
40
50
Bayesian Statistics
likelihood
posterior
Bayes’ Rule •
prior
PD | M PM 
PM | D  
PD 
marginal
M: the model, D: data or evidence •
PD    PD | M PM   discrete
  PD | M PM dM  continuous
Basic Bayesian Statistics
Bayes’ Rule is at the heart of much predictive •
software
In the simplest example, we can simply compare two •
models, and reduce it to a log-odds ratio
P M1 data 
P data M1 
P M1 
log
 log
 log
P M 2 data 
P data M 2 
P M 2 
Prokaryotes HMMs: Taking Overlaps on
Two Strands into Account
overlap 3
Genetic +
short +
Termination +
overlap 1
Initiation +
overlap 2
intergenic
Termination -
Initiation -
short Genetic -
overlap 0
Coding region (genes)
overlap 3
Genetic +
short +
Termination +
overlap 1
Initiation +
overlap 2
intergenic
Termination -
Initiation -
short Genetic -
overlap 0
Coding region (genes)
A
A
A
A
A
C
A
G
A
Model of
….
….
….
all
possible
64 codons
T
T
T
Transition
from any
codon to
any other.
Model Design (3)
Integenic regions and overlap regions:
 Two consecutive genes either overlap each other or separated by an itergenic region.
 The overlaping segment or the intergenic region is bordered in one of 4 possible ways.
Intermediate intergenic region
Tail
Tail–Head
Head–Tail
Tail–Tail
Head–Head
5'
3'
5'
3'
5'
3'
5'
3'
Overlapping Region
Head
3'
5'
3'
5'
3'
5'
3'
5'
5'
3'
5'
3'
5'
3'
5'
3'
3'
5'
3'
5'
3'
5'
3'
5'
Example 1
5'
3'
3'
5'
Transition between two
genes on the same strand.
overlap 3
Genetic +
short +
Termination +
overlap 1
Initiation +
overlap 2
intergenic
Termination -
Initiation -
short Genetic -
overlap 0
Example 2
5'
3'
3'
5'
Two genes on the opposite
strands.
overlap 3
Genetic +
short +
Termination +
overlap 1
Initiation +
overlap 2
intergenic
Termination -
Initiation -
short Genetic -
overlap 0
Transitions between genes
5'
3'
3'
5'
overlap 3
Genetic +
short +
Termination +
overlap 1
Initiation +
overlap 2
intergenic
Termination -
Initiation -
short Genetic -
overlap 0
Intergenic Regions
Intergenic regions are modeled by
profile HMMs.
5'
3'
3'
5'
We model two different types of intergenic regions:
1. Short intergenic sequences:
 9 bases long.
 Model situations where two same strand genes are close together.
 This situation is common in polycistronic operons.
2. Long intergenic sequences are the more common case.
They are modeled by the following 2 profile HMMs:
 Transcription termination signal: 18 bases long.
 Promoter region including the Shine-Dalgarno signal: 25 bases long.
Overlap Regions (1)
Overlap regions of 1 or 4 bases:
Weight matrix models[i] (WMM) are used to represent overlapping regions of 1 or 4 bases,
consisting of the stop codon of the previous gene and the start codon of the next one.
.
 1 base overlap of stop codon TAA or TGA, with init codon ATG:
A
C
G
T----
T A A T G
bases
A-C
G-T
A---C
G
T
A
C
G
T----
A
C
G---T
WMM format
 4 bases overlap: First gene terminated by TGA, second gene starts with [AG]TG:
N N A T G A N N
bases
ACGT-
ACGT-
A--C
GT
A
C
G
T----
A
C
G---T
WMM format
A---C
G
T
ACGT-
ACGT-
Overlap Regions (2)
Overlap regions of 6 or more bases:
For each one of the 4 possible paths described (headhead, head  tail, tail  tail,
tailhead), all possible frame differences are allowed.
For example: a tailhead transition allows a 1 or 2 bases' shift of the reading frame.
Frame 1
Stop codon
Frame 2
Frame 1
Init
codon
Frame 2/3
Frame 3
Init
codon
Frame 1
Stop codon
5'
3'
3'
5'