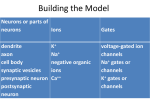
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Neural Coding: Higher Order Temporal Patterns in the
Types of artificial neural networks wikipedia , lookup
Mirror neuron wikipedia , lookup
Development of the nervous system wikipedia , lookup
Neural oscillation wikipedia , lookup
Central pattern generator wikipedia , lookup
Neuroanatomy wikipedia , lookup
Metastability in the brain wikipedia , lookup
Neuropsychopharmacology wikipedia , lookup
Premovement neuronal activity wikipedia , lookup
Neural coding wikipedia , lookup
Circumventricular organs wikipedia , lookup
Inductive probability wikipedia , lookup
Neural modeling fields wikipedia , lookup
Time series wikipedia , lookup
Biological neuron model wikipedia , lookup
Pre-Bötzinger complex wikipedia , lookup
Optogenetics wikipedia , lookup
Feature detection (nervous system) wikipedia , lookup
Synaptic gating wikipedia , lookup
Nervous system network models wikipedia , lookup
Neural Coding: Higher Order Temporal Patterns in the Neurostatistics of Cell Assemblies Laura Martignon Max Planck Institute for Human Development Lentzeallee 94, 14195 Berlin [email protected] Gustavo Deco Siemens AG Corporate Technology ZT Otto Hahn Ring 6, 81739 Munich [email protected] Kathryn Laskey Dept. of Systems Engineering George Mason University Fairfax, VA [email protected] Mathew Diamond Cognitive Neuroscience Sector International School of Advanced Studies Via Beirut, 9 34014 Trieste [email protected] Winrich Freiwald Dept. of Neurophysiology Max-Planck-Institute for Brain Research D-60528Frankfurt/M. [email protected] Eilon Vaadia Dept. of Physiology The Hebrew University of Jerusalem Jerusalem 91010 [email protected] Abstract Recent advances in the technology of multi-unit recordings make it possible to test Hebb’s hypothesis that neurons do not function in isolation but are organized in assemblies. This has created the need for statistical approaches to detecting the presence of spatiotemporal patterns of more than two neurons in neuron spike train data. We examine three measures for the presence of higher order patterns of neural activation -- coefficients of log-linear models, connected cumulants, and redundancies -- and present arguments in favor of the coefficients of log-linear models. We present test statistics for detecting the presence of higher order interactions in spike train data. We also present a Bayesian approach for inferring the existence or absence of interactions and estimating their strength. The two methods are shown to be consistent in the sense that highly significant correlations are also highly probable. A heuristic for the analysis of temporal patterns is also proposed. The methods are applied to experimental data, to synthetic data drawn from our statistical models, and to synthetic data produced from biologically plausible simulations of neural activity. Our experimental data are drawn from multi-unit recordings in the somato-sensory cortex of anesthetized rats obtained by Diamond, from multi-unit recordings in the frontal cortex of behaving monkeys obtained by Vaadia and from multi-unit recordings in the visual cortex of behaving monkeys obtained by Freiwald. 1 Introduction Hebb conjectured that information processing in the brain is achieved through the collective action of groups of neurons, which he called cell assemblies (Hebb, 1949). One of the assumptions on which he based his argument was his other famous hypothesis that excitatory synapses are strengthened when the involved neurons are frequently active in synchrony. Evidence in support of this, so called ”Hebbian learning” hypothesis has been provided by a variety of experimental findings over the last three decades (see for instance, Rauschecker, 1991). Evidence for collective phenomena confirming the ”cell assembly” hypothesis has only recently begun to emerge as a result of the progress achieved by multi-unit recording technology. Hebb’s followers had been left with a twofold challenge: • to provide an unambiguous definition of cell assemblies. • to conceive and carry out the experiments that demonstrate their existence. Cell assemblies have been defined in various ways, both in terms of anatomy and of shared function. One persistent approach characterizes the cell assembly by near-simultaneity or some other specific timing relation in the firing of the involved neurons. If two neurons converge on a third one, their synaptic influence is much larger for near-coincident firing, due to the spatiotemporal summation in the dendrite (Abeles, 1991; Abeles, Bergman, Margalit and Vaadia, 1993). Thus syn-firing and other specific temporal relationships between active neurons have been posited as mechanisms by which the brain codes information (Singer, 1994; Abeles and Gerstein, 1998; Abeles, Prut, Bergman and Vaadia, 1994; Prut, Vaadia, Bergman, Haalman and Slovin, 1993). In pursuit of experimental evidence for cell assembly activity in the brain, physiologists thus seek to analyze the activation of many separate neurons simultaneously, preferably in awake, behaving animals. These ”multi-neuron activities” are then inspected for possible signs of interactions between neurons. Results of such analyses may be used to draw inferences regarding the processes taking place within and between hypothetical cell assemblies. The conventional approach is based on the use of cross correlation techniques, usually applied to the activity of pairs (sometimes triplets) of neurons recorded under appropriate stimulus conditions. The result is a time-averaged measure of the temporal correlation among the spiking events of the observed neurons under those conditions. Application of these measures has revealed interesting instances of time- and context-dependent synchronization dynamics in different cortical areas. For interactions among more than two neurons, Gerstein, Perkel and Dayhoff (1985) devised the so called gravity method. Their method views neurons as particles that attract each other and measures simultaneously the attractions between all possible pairs of neurons in the set. The method, although it allows one to look at several neurons globally, does not account for nonlinear synapses nor for synchronization of more than two neurons. Recent investigations have focused on the detection of individual instances of synchronized activity called ”unitary events” (Grün, 1996; Grün, Aertsen, Vaadia and Riehle, 1995) between groups of two and more neurons. Of special interest are patterns involving three or more neurons, which cannot be described in terms of paircorrelations. Such patterns are genuine higher order phenomena. The method developed by Prut, Vaadia, Bergman, Haalman, Slovin and Abeles (1998) for detecting precise firing sequences of up to three units adopts this view, subtracting from three-way correlations all possible pair correlations. The models reported in this paper were developed for the purpose of describing and detecting higher order correlations of any order in a unified way. In the data we analyze, the spiking events (in the 1 m/sec range) are encoded as sequences of 0's and 1's, and the activity of the whole group is described as a sequence of binary configurations. This paper presents a family of statistical models for analyzing such data. In our models, the parameters represent spatiotemporal firing patterns. We generalize the spatial correlation models developed by Martignon et al., (Martignon, v. Hasseln, Grün, Aertsen and Palm, 1995), (Laskey & Martignon, 1996) to include a temporal dimension. We develop statistical tests for detecting the presence of a genuine order-n correlation and distinguishing it from an artifact that can be explained by lower order interactions. The tests compare observed firing frequencies on the involved neurons with frequencies predicted by a distribution that maximizes entropy among all distributions consistent with observed information on synchrony of lower order. We also discuss a Bayesian approach in which hypotheses about interactions on a large number of subsets can be compared simultaneously. We compare our log-linear models with two other candidate parameters of higher order correlations. One of these candidates, drawn from statistical physics, is the connected cumulant. The other, drawn from information theory, is mutual information or redundancy. We argue that the coefficients of log-linear models, or effects, provide a more natural measure of higher order phenomena than either of these alternate approaches. We present the results of analyzing synthetic data generated from our models. These synthetic data provide a test of the performance of our statistical methods on data of known distribution. We also present results for synthetic data provided by the experimenter. These synthetic data permit us to evaluate the ability of our models to detect known structure and avoid detecting spurious structure in data generated by biologically plausible models. Finally, results are presented from applying the models to multi-unit recordings in the frontal cortex of monkeys obtained by Vaadia and multi-unit recordings in the somato-sensory cortex of rats obtained by Diamond. 2 Measures for Higher Order Synchronization The term spatial correlation has been used to denote synchronous firing of a group of neurons, while the term temporal correlation has been used to indicate chains of firing events at specific temporal intervals. Terms like "couple" or "triplet" have been used to denote spatiotemporal patterns of two or three neurons (Abeles et al., 1993; Grün, 1996) firing simultaneously or in sequence. Establishing the presence of such patterns is not straightforward. For example, three neurons may fire together more often than expected by chance1 without exhibiting an authentic third order interaction. For example, if a neuron participates in two couples, such that each pair fires together more often than by chance, then the three involved neurons will fire together more often than the independence hypothesis would predict. This is not, however, a genuine third-order phenomenon. Authentic triplets, and, in general, authentic n-th order correlations, must therefore be distinguished from correlations that can be explained in terms of lower order correlations. We introduce log-linear models for representing firing frequencies on a set of neurons and show that nonzero coefficients or effects of these log-linear models are a natural measure for synchronous firing. We argue that effects of log-linear models are superior to other candidate approaches drawn from statistical physics and information theory. In this section we consider only models for synchronous firing. Generalization to temporal and spatiotemporal effects is treated in Section 3. 2.1 Effects or Coefficients of Log-Linear Models Consider a set of n neurons. Each neuron is modeled as a binary unit that can take on one of two states: 1 (”firing”) or 0 (”silent”). The state of the n units is represented by the vector x =(x 1 ,…,x n ), where each x i can take on the value zero or one. There are 2n possible states for the n neurons. If all neurons fire independently of each other, the probability of configuration x is given by p(x 1,K, x n ) = p(x1 )L p(x n ) (1) Methods for detecting correlations look for departures from this model of independence. Neurons are said to be correlated if they do not fire independently. A correlation between two neurons, labeled 1 and 2, is expressed mathematically as p(x 1, x 2 ) ≠ p(x1 ) p(x 2 ) 1 That is to say, more often than predicted by the hypothesis of independence. (2) Extending this idea to larger sets of neurons introduces complications. It is not sufficient simply to compare the joint probability p(x 1 ,x 2 ,x 3 ) with the product p(x 1 )p(x 2 )p(x 3 ) and declare the existence of a triplet when the two are not equal. This would confuse authentic triplets with overlapping doublets or combinations of doublets and singlets. Thus, neurons 1, 2, and 3 may fire together more often than the independence model (1) would predict because neurons 1 and 2, and neurons 2 and 3, are each involved in a binary interaction (Figure 1). • 1 • • 1 3 •2 a. Overlapping Pairwise Correlations •3 •2 b. Authentic Third-Order Correlation Figure 1: Overlapping Doublets and Authentic Triplet Equation (2) expresses in mathematical form the idea that two neurons are correlated if the joint probability distribution for their states cannot be determined from the two individual probability distributions p(x 1 ) and p(x 2 ). Now consider a set of three neurons. The probability distributions for the three pair configurations are p(x 1 ,x 2 ), p(x 2 ,x 3 ), and p(x 1 ,x 3 ). 2 A genuine third-order interaction among the three neurons would occur if it were impossible to determine the joint distribution for the three-neuron configuration using only information on these pair distributions. A canonical way to construct a joint distribution on three neurons from the pair distributions is to maximize entropy subject to the constraint that the two-neuron marginal distributions are given by p(x 1 ,x 2 ), p(x 2 ,x 3 ), and p(x 1 ,x 3 ). This is the distribution that adds the least information beyond the 2 Note that these pairwise distributions also determine the single-neuron firing frequencies p(x 1), p(x 2), and p(x 3), which can be expressed as their linear combinations. information contained in the pair distributions. It is well known3 that the joint distribution thus obtained can be written as p(x 1, x 2 , x 3 ) = exp{θ0 +θ 1 x1 + θ 2 x 2 + θ 3 x 3 + θ 12 x1 x2 +θ 13 x1 x 3 + θ 23 x2 x3 } , (3) where the θ’s are real-valued parameters, and where θ 0 is determined from the other θ’s and the constraint that the probabilities of all configurations sum to 1. In this model, there is a parameter for each individual neuron and for each pair of neurons. Each of these parameters, which in the statistics literature are called effects, can be thought of as measuring the tendency to be active of the neuron(s) with which it is associated. Increasing the value of θ i without changing any other θ’s increases the probability that neuron i is in its ”on” state. Increasing the value of θ ij without changing any other θ’s increases the probability of simultaneous firing of neurons i and j. It is instructive to note that there is a second-order correlation between neurons i and j in the sense of (2) precisely when θ ij≠0. Not all joint probability distributions on three neurons can be written in the form of (3). A general joint distribution for three neurons can be expressed by including one additional parameter:4 p(x 1, x 2 , x 3 ) = exp{θ0 +θ 1 x1 + θ 2 x 2 + θ 3 x 3 + θ 12 x1 x2 +θ 13 x1 x 3 + θ 23 x2 x3 + θ 123 x1 x 2 x 3 } (4) Holding the other parameters fixed and increasing the value of θ 123 increases the probability that all three neurons fire simultaneously. Equation (3) corresponds to the special case of (4) in which θ 123 3 4 See, for example, Good (1963) and also Bishop, Fienberg and Holland (1975). This can be seen by noting that log p(x 1,x 2,x 3) can be expressed as a set of linear equations relating the configuration probabilities to the θ’s. These equations give a unique set of θ’s for any given probability distribution. is equal to zero, just as independence corresponds to the special case of (3) in which all secondorder terms θ ij are equal to zero. It seems natural, then, to define a genuine order-3 correlation as a joint probability distribution that cannot be expressed in the form of (3) because θ 123 ≠0. As will be shown below in Section 3, this idea can be extended naturally to larger sets of neurons and to temporal patterns. Parameterizations of the general form (3) and (4) are called log-linear models because the logarithm of the probabilities can be expressed as a linear sum of functions of the configuration values. They obviously correspond to the coefficients of the energy expansions of generalized Boltzmann machines in statistical mechanics (Amari, 1992). The coefficients of the log-linear model are called effects. A joint probability distribution on n neurons is represented as a log-linear model in which parameters are associated with subsets of neurons. A genuine n-th order correlation on a set A of n neurons is defined in terms of a log-linear model in which the parameter θ A associated with the set A is not equal to zero. The information-theoretic justification for our proposed definition of higher order interaction is theoretically satisfying. But if the idea is to have practical utility, we require a method for measuring the presence of genuine correlations and distinguishing them from noise due to finite sample size. Fortunately, there is a large statistical literature on estimation and hypothesis testing using log-linear models. In the following sections, we discuss ways to detect and quantify the presence of higher order correlations. We also apply the methods to real and synthetic data. 2.2 Other Measures for Higher Order Correlation We mention two further approaches to measuring the existence of higher order correlations in a set of binary neurons. Connected cumulants, a measure of higher order correlation used in statistical mechanics, have been proposed by Aertsen (Aertsen, 1992) as a candidate parameter for spatiotemporal patterns of neural activation. Mutual information has been proposed by Grün (1996). For two neurons with configurations denoted by (x 1 ,x 2 ) the connected cumulant is given by C123 = x1x 2 − x1 x 2 (5) while for three neurons the corresponding formula is C123 = x1x 2x 3 − x1 x 2x 3 − x 2 x1x3 − x3 x1x 2 + 2 x1 x2 x3 (6) In these expressions, the symbol <⋅ > stands for expectation. For the single i-th neuron indexed by <x i > is the expected firing frequency. For a set of k neurons, < x1 ,x2 ,...x k > is the expected frequency with which the corresponding k neurons are simultaneously active. The general formula of cumulants can be obtained by induction by means of the following construction rule: products C1,2 ,...,N = x1 ...x N − ∑ Ci1 of ...iM connected cumulants . where M <N In the case of two neurons, the absence of correlation defined by means of cumulants is equivalent to the absence of correlation established by the effects of log-linear models. That is, the connected cumulant is equal to zero if and only if the neurons exhibit no interaction as defined by (2). For three or more neurons things change. From (6) it can be shown that the connected cumulant may be nonzero when there exist overlapping couples as shown in Figure 1. Such overlapping couples, we argue, constitute a second-order phenomenon and not a true third-order interaction. The thirdorder term of a log-linear model, in contrast, will be equal to zero for Figure 1a and nonzero for Figure 1b. Thus, we argue that the effects of log-linear models are a better measure for authentic higher order interactions. Another approach to measuring higher-order correlations is drawn from information theory. Grün (Grün, 1996) proposed the use of mutual information to characterize higher order phenomena. The mutual information measure (Cover & Thomas, 1991) for two neurons is given by I(x1; x2 ) = ∫ P(x1,x 2 ) log( p(x1, x 2 ) )dx dx p(x1 )p(x2 ) 1 2 (7) = H(x1 ) + H(x2 ) − H(x1, x 2 ) where H(x1 ,xn ) denotes the joint Shannon entropy (Cover and Thomas, 1991). The mutual information of two neurons is zero if and only if the neurons are stochastically independent. Therefore, departures of (7) from zero measure correlation between pairs of neurons. The measure (7) can be extended to three neurons as p(x ,x ,x ) 1 2 3 ) I(x1 ;x2 ;x 3 ) = ∫ dx dx dx P(x ,x ,x )log( 1 2 3 1 2 3 p(x ) p(x )p(x ) 1 2 3 = H(x ) + H(x ) + H(x ) − H(x ,x ,x ) 1 2 3 1 2 3 (8) Mutual information as defined by (8) measures departures from independence and not true thirdorder correlation. Therefore, it too is unable to distinguish true higher order correlation from correlation due to lower order phenomena. 3 A Mathematical Model for Spatiotemporal Firing Patterns The previous section described several approaches to generalizing the concept of pairwise correlations to larger numbers of neurons. Coefficients of log-linear models were proposed as a measure of higher order correlations and justified by their ability to distinguish true higher order correlations from apparent correlations that can be explained in terms of lower order correlations. For clarity of exposition, the discussion was limited to synchronous firing on groups of two and three neurons. In this section, we generalize the approach to arbitrary numbers of neurons and to temporal correlations. Consider a set Λ of n binary neurons and denote by p the probability distribution on sequences of binary configurations of Λ . Assume that the sequence of configurations x t = (x1t ,L, xnt ) of n zneurons forms a Markov chain of order r. Let δ be the time step, and denote the conditional distribution for x t given previous configurations by p(x t | x (t−δ ) , x (t −2 δ) ,..., x (t − rδ) ) . We assume that all transition probabilities are strictly positive and expand the logarithm of the conditional distribution as p( x | x t ( t −δ ) ,x ( t−2δ ) ,...,x ( t −r δ ) ) = exp{θ + ∑ θ X } 0 A ∈Ξ A A (9) In this expression, each A is a subset of pairs of subscripts of the form (i,t − sδ) for r≥s≥0 that includes at least one pair of the form (i,t ). The variable x A = ∏ x(i j ,t −m j δ) is equal to 1 in the 1≤ j ≤k event that all neurons in A are active and zero otherwise. The set Ξ⊆2Λ for which θ A ≠0 is called the interaction structure for the distribution p. The parameter θ A is called the interaction strength for the interaction on subset A. Clearly, θ Α =0 means A∉Ξ and is taken to indicate absence of an order-|A| interaction among neurons in A. We denote the structure-specific vector of nonzero nteraction strengths by θ Ξ. Definition 1: We say that neurons {i1 ,i2 ,..., ik } exhibit a spatiotemporal pattern if there is a set of time intervals m1 δ,m2 δ,..., mk δ with r≥mi≥0 and at least one mi = 0 , such that θ A ≠ 0 in (1), where A = {(i1 ,t − m1 δ),...,(ik ,t − mk δ)}. Definition 2: A subset {i1 ,i2 ,..., ik } of neurons exhibits a synchronization or spatial correlation if θ A ≠ 0 for A={(i1 , 0),...,(ik ,0) }. In the case of absence of any temporal dependencies the configurations at different times are independent and we drop the time index: p(x) = exp{θ 0 + ∑θ A x A } (10) where each A is a nonempty subset of Λ and x A = ∏ x i . i∈A Of course, we expect temporal correlation of some kind to be present, one such example being the refractory period after firing. Nevertheless, (10) may be adequate in cases of weak temporal correlation and generalizes naturally to the situation of temporal correlation. Increasing the bin width can result in temporal correlations of short time intervals manifesting as synchronization. It is clear that (3) and (4) are special cases of (9) for the case of three neurons and no temporal dependence. The interaction structure Ξ for (4) consists of all non-empty subsets of neurons. For (3) the interaction structure consists of all single-neuron and two-neuron subsets. Although the models (9) and (10) are statistical, not physiological, one would naturally expect synaptic connection between two neurons to manifest as nonzero θ A for the set A composed of these neurons with the appropriate delay. One example leading to nonzero θ A in (10) would be simultaneous activation of the neurons in A due to common input (Figure 2a). Another example is simultaneous activation of overlapping subsets covering A, each by a different unobserved input (Figure 2b). An attractive feature of our models is that the two cases of Figure 2 can be distinguished when the neurons in A exhibit no true lower order interactions. Suppose a model of the form (2) is constructed for all neurons, both observed and unobserved. The model of Figure 2a corresponds to a log-linear expansion with only individual neuron coefficients and the fourth-order effect θ H123 , where H is a hidden unit, as in Figure 2. The model of Figure 2b contains individual neuron effects and the triplet effects θ H12 and θ K23 , where K is another hidden unit different from H. When the probabilities are summed over the unobserved neurons to obtain the distribution over the three observed neurons, both models will contain third-order coefficients θ 123 . However, the model of Figure 2a will contain no nonzero second-order coefficients, while the model of Figure 2b will contain nonzero coefficients of all orders up to and including order 3. Thus log-linear models have the desirable feature that the existence of a nonzero θ A coupled with θ B =0 for B ⊂ A indicates a correlation among the neurons in A possibly involving unobserved neurons. On the other hand, a nonzero θ A together with θ B ≠0 for B ⊂ A may be explained away by interactions involving subsets of A and unobserved neurons. The probability distribution p* that maximizes entropy among distributions with the same marginals as the distribution p on proper subsets of A has a log-linear expansion in which only θ B , B ⊂ A, B ≠ A are nonzero. 1 • H • 1 • • 2 5 • • • 4 H 5 2 • K 6 • • •4 3 A • Λ a. θ 123 ≠0, θ 12 =θ 23 =0 • • 6 3 • A Λ b. θ 123 ≠0, θ 12 ≠0, θ 23 ≠0 Figure 2: Nonzero θ 123 Due to Common Hidden Inputs H and/or K 4 Estimation and Testing Based on Maximum Likelihood Theory We consider two general approaches to estimating the correlation structure in a set of neurons. The first approach is based on maximum likelihood theory. Interaction strength parameters are estimated by the method of maximum likelihood and structures are compared using likelihood ratio tests. This approach is grounded in the frequentist school of statistical inference. The second approach, described in the following section, is based on the Bayesian school of statistics. Before presenting the maximum likelihood methods, we take a brief digression to present the frequentis t approach to statistical inference and distinguish it from the Bayesian approach. The frequentist school of statistics grew up in the early part of this century, and has its roots in positivism and the accompanying philosophical stance that science should strive for strict objectivity. Frequentist statistics has its theoretical foundation in the work of von Mises (1939) and the pioneering work of Neyman and Pearson (1928). In frequentist statistics, one views the parameters of statistical models as objective unknowns that are not directly observable, about which one can draw inferences on the basis of observable random variables whose distributions depend on the parameters. Thus, one cannot directly observe the probability that a coin will turn up heads or that a neuron will fire, but one can observe a large sample of coin tosses or a large number of time bins of neural recording, from which one can estimate the probability in question. Frequentists take the philosophical position that only objectively random phenomena can be assigned probabilities. Thus, it is incorrect to assign a probability to an individual toss of a coin, an individual sample on a neuron, or any other one-time event. Probabilities are assigned to hypothetically infinite collectives of repeatable events, such as a series of coin tosses or a series of multi-unit recordings made under identical conditions. The probability distribution of (9) (or in the case of absence of temporal correlation, (10)) can be estimated by the empirical frequency distribution obtained via a sample taken from multi-unit recordings. From this empirical distribution, estimates of the θ’s can be obtained by solving a system of linear equations relating the logarithms of the frequencies to the θ’s. Although straightforward, this naive approach leads to difficulties. These difficulties arise because of instability in the parameter estimates due to statistical variation in the empirical frequency distribution. In other words, if the same recording procedure were applied multiple times under identical conditions to the identical animal, the results of the recordings would differ from each other and from the assumed underlying ”true” probability distribution, simply due to chance fluctuations. Therefore, even if θ A=0, we would expect an estimate derived from empirical frequency data to differ from zero. It is important to be able to tell true correlations from estimates θ A that are different from zero by chance. If the observed data arise from either (9) or (10), the Law of Large Numbers implies that as the sample size grows sufficiently large, the observed frequencies of coincident firing of neurons in the set A eventually converge to the true probability of coincident firing as given by the model. The theory of maximum likelihood implies that the maximum likelihood estimates of the θ’s also converge to their true values. Statistical hypothesis tests can be constructed to evaluate whether a particular nonzero estimate θˆ A can be explained by a chance fluctuation in a model with true θ A equal to zero. Estimation and hypothesis testing are complicated by instability due to the presence of a large number of parameters to be estimated and/or hypotheses to be tested simultaneously. The dimension of (9) is exponential in the number of neurons times the order of the Markov chain, and (10) is exponential in the number of neurons. The estimates of θ A and θ B are correlated for overlapping subsets A and B. This means that the number of observations required for stable estimates for all θ’s grows rapidly with the number of neurons and the order of the Markov chain. 4.1 Statistical Tests Based on Maximum Likelihood Theory We are interested in the problem of detecting nonzero θ A for subsets A of neurons in a set of n neurons whose firing frequencies are governed by model (9) or (10). That is, for a given set A, we are interested in testing which of the two hypotheses H0 : θ A=0 H1 : θ A≠0 is the case. The hypothesis H0 is called the null hypothesis and H1 is called the alternative hypothesis. Generally, the hypothesis selected as the null hypothesis is regarded as having the benefit of the doubt, and the alternative hypothesis must bear the burden of proof. That is, we wish to reject the null hypothesis in favor of the alternative hypothesis only when the experimental results are unlikely to have been observed if the null hypothesis is true. In our situation, it seems reasonable to take the hypothesis θ A=0 as the null hypothesis against the alternative θ A≠0. That is, we wish to declare the existence of a higher order interaction only when the observed correlations are unlikely to be a chance result of a model in which θ A=0. In the theory of statistical hypothesis testing (Neyman & Pearson, 1928), one constructs a test statistic whose distribution is known under the null hypothesis. Then one chooses a critical range of values of the test statistic that are highly unlikely under the null hypothesis but are likely to be observed under plausible deviations from the null hypothesis. If the observed value of the test statistic falls into the critical range, one rejects the null hypothesis in favor of the alternative hypothesis. Consider the problem of testing θ A≠0 against θ A=0 in the log-linear model (10) for synchronous firing in observations with no temporal correlation. A reasonable test statistic is the likelihood ratio statistic, denoted by G2 . To construct the G2 test statistic, we first obtain the maximum likelihood estimate of the parameters θ under the null and alternative hypotheses. We construct our test statistic by conditioning on the silence of neurons outside A. The maximum likelihood estimate of θ under the null hypothesis is then obtained by setting the frequency distribution p1 (x ) over configurations of neurons in the set A to the sample frequencies and solving for θ . The maximum likelihood estimate for θ under the null hypothesis may be obtained by a standard likelihood maximization procedure such as iterative proportional fitting (IPF), or by a simple one-dimensional optimization procedure described below, which we call the Constraint Perturbation Procedure (CPP). From the estimate of θ , one can solve for the estimated configuration probabilities p0 (x ) for the null hypothesis. Using these probability estimates, we compute the likelihood ratio test statistic G 2 = 2N ∑ p1 (x)(ln p1(x) − ln p0 (x)) (11) x where N is the sample size for the test (the number of configurations in which neurons outside of A are silent). As the sample size for the test tends to infinity, the distribution for this test statistic under p0 tends to a chi-squared distribution, where the number of degrees of freedom is the difference in the number of parameters in the two models being compared. In this case the larger model has a single extra parameter, so the reference distribution has one degree of freedom. The interpretation of test results is as follows. If the value of the test statistic is highly unusual for a chisquared distribution with one degree of freedom, this casts doubt on the null model p0 and is therefore regarded as evidence that the additional parameter θ A is nonzero. Discarding observations for which neurons outside A are active simplifies the construction of a test statistic for θ A=0. It is easy to see that the distribution of the test statistic does not depend on whether there are nonzero order-|A| or higher coefficients other than θ A . The power of a test is reduced over a test based on all the observations.5 In our data this is not a major difficulty because overall firing frequencies are low. An alternative approach would be to construct a test using all the data, in which the null hypothesis is that all coefficients of order |A| or larger are zero and the alternate hypothesis is that all order-|A| or higher coefficients except θ A are zero. Both of these tests suffer from a common difficulty that arises in high-dimensional statistical problems. We usually are not interested in inference about one specific coefficient θ A. Rather, we are interested in the question of which coefficients are nonzero. In other words, the hypothesis testing procedure is applied repeatedly for a large number of sets A. Although the significance level (probability of incorrectly rejecting a true null hypothesis) may be low for each test individually, if enough tests are performed one expects some spurious results. Thus, it is important not to take significance levels at face value when performing multiple repeated hypothesis tests. 6 Nevertheless, we regard statistical significance of a coefficient as evidence for existence of correlation of the associated neurons. 4.2 The Constrained Perturbation Procedure In this section we construct the null hypotheses for the tests proposed above. Assume again that p is a probability distribution defined on the configurations of a set A of vertices. Consider the following problem: Find a distribution p* such that 1. the marginals of order less than A of p* coincide with those of p. 5 A statistical hypothesis test has a high power if the probability of correctly rejecting a false null hypothesis is high, and high significance if the probability of incorrectly rejecting a true null hypothesis is low. 6 There exist adjustments to significance tests to account for multiple comparisons, which we do not develop formally in this paper. 2. p* maximizes entropy among all distributions whose marginals of order less than A coincide with those of p. This problem has a unique solution. In fact, this solution coincides with the unique distribution whose marginals of order less than A coincide with those of p such that θ *A = 0, where θ*A is the coefficient corresponding to A in the log-expansion of p. This was proven by Good (1963) in the early sixties (for a proof of the uniqueness of the solution see Whittaker 1989). In what follows we explicitly construct a solution. If B is a nonempty subset of A , denote by χ B the configuration that has a component 1 for every index in B and 0 elsewhere. Define p* ( χ B ) = p( χ B ) + ( −1)| B| ∆ , where ∆ is to be determined by solving for θ*A ≡ 0 among probability distributions. As we have observed, θ*A can be written as θ* = ∑ ( −1) | A− B| A B⊂ A lnp* ( χ ) . B (12) Furthermore, define p* ( 0) = 1 − ∑ p* ( χ B ) . This distribution p* has the required properties. φ≠ B ⊂A It maximizes entropy among those with the same marginals of p on proper subsets of A . Example 2. Suppose that A = V={1,2,3} and that p is a strictly positive distribution on A . We want to construct the distribution p* that maximizes entropy among all those consistent with the marginals of order 2, denoted by Marg.({{1,2},{1,3},{1,3}}).7 Define p*(1,1,1) = p(1,1,1) - ∆ p*(1,1,0) = p(1,1,0) + ∆ p*(1,0,1) = p(1,0,1) + ∆ p*(1,0,0) = p(1,0,0) - ∆ 7 Observe that by fixing the second-order marginals, we are also fixing first-order marginals, which are their linear combinations. p*(0,1,1) = p(0,1,1) + ∆ p*(0,1,0) = p(0,1,0) - ∆ p*(0,0,1) = p(0,0,1) - ∆ p*(0,0,0) = 1 - ∑ p( χ B ) B⊂{1,2 ,3 } It is possible to see at a glance that all second-order marginals of p* coincide with those of p. The only additional step we need to undertake is to solve for ∆ in the equations θ*A = 0. Observe that our construction contains only one step where a numerical approximation becomes necessary, namely solving for θ*A =0 in terms of ∆ . This can be done by using any one-dimensional optimization procedure such as Newton’s approximation method8 . Newton's approximation method has to be used in combination with the conditions that the perturbation ∆ is such that all candidate solutions are probability distributions and thus their values are between 0 and 1. 5 Statistical Tests Based on Bayesian Model Comparison An alternative approach to the Neyman & Pearson hypothesis testing described in 4.1 is Bayesian estimation. The Bayesian approach is gaining in favor as computational methods for obtaining Bayesian estimates grow in maturity. Before moving in Section 5.1 to a detailed treatment of the Bayesian approach to our problem, a digression is necessary to discuss the Bayesian attitude in statistics, how it differs from the frequentist attitude, and why it is especially appropriate for problems like that treated in this paper. The Bayesian school of statistics is named after its originator, the Reverend Thomas Bayes (16961761). In the Bayesian view, probability is a theory of belief dynamics. A probability is a number Any one-dimensional optimization procedure can be used to solve the problem: Find ∆ such that θ*A = 0, or equivalently, such that the resulting probability distribution maximizes entropy in the manifold of probability distributions whose marginals of order less than A coincide with those of p 8 that can be attached to any uncertain proposition and measures the degree to which that proposition is believed to be true. When additional evidence is obtained about the proposition, beliefs are updated according to the probability calculus, so that a prior probability distribution is transformed into a posterior probability distribution that reflects how beliefs have been revised in the light of the new evidence. Most modern Bayesians are subjectivists. That is, they view probabilities as subjective and adopt the stance that rational individuals may disagree about the probability to be attached to a proposition.9 For collectives of events that a frequentist would model as random and be willing to assign a probability distribution, de Finetti’s Theorem (de Finetti, 1937) shows that with enough evidence any nondogmatic subjectivist10 will converge to nearly the same probability estimate as a frequentist’s. Standard frequentist methods may run into difficulties on high-dimensional problems such as the one treated in this paper. In contrast, high-dimensional problems pose no essential difficulty in the Bayesian approach, as long as prior distributions are chosen appropriately. In the Bayesian framework, the prior distribution can be thought of as a bias that keeps the model from jumping to inappropriately strong conclusions. In our problem, then, we assign prior distributions that bias the model toward the hypothesis that ”effects, that is, coefficients of the log-linear model, are zero”. Inferences by the model that “a parameter is nonzero” indicate reasonably strong observational evidence against the hypothesis that “the parameter is zero”. Another advantage of the Bayesian approach we take in this paper is that nonnested hypotheses pose no special difficulty. In the Bayesian approach, we begin by assigning a prior distribution to the vector θ of parameters of the log-linear model. In our prior distribution, we assume that all θ A are independent of each 9 It is likely that early probabilists such as Pascal, Bernoulli, and Laplace did not distinguish between the frequentist, subjectivist, and logical views of probability but assumed that all rational individuals with the same information would agree on the ”correct” probability to be attached to a proposition, and that with enough evidence would come to agree on an estimate near the true probability. 10 That is, one who does not place probability zero on a region including the correct parameter value. other. We also assume that each θ A is probably equal to zero but has a small probability of being nonzero. We then assume a continuous probability density for θ A conditional on its being nonzero, in which values very different from zero are less likely than values near zero. This prior distribution assigns a probability to each interaction structure Ξ, in which the interaction structures containing fewer subsets are most likely. A sample of observations from multi-unit recordings is used to update the prior distribution and obtain a posterior distribution. The posterior distribution also assigns a probability to each interaction structure and a continuous probability structure to the nonzero θ A given the interaction structure. The posterior probability that θ A≠0 is the sum of the probability of all interaction structures in which θ A≠0. Thus, there is no need to choose a specific null hypothesis against which to test -- the Bayesian approach automatically tests all hypotheses in which θ A≠0 against all hypotheses in which θ A=0. The major difficulty with the Bayesian approach is its computational complexity. With n neurons and considering only synchronicity with no temporal correlation, there are 2 2 n interaction structures to consider. Clearly, it is infeasible to enumerate all of these. In Section 5.1 we discuss Markov Chain Monte Carlo sampling approaches designed for this type of high-dimensional problems. These approaches still have a high computational cost, and we are working on heuristics to increase the efficiency of sampling. 5.1 Detecting Synchronizations in the Bayesian Approach We begin with the problem of determining synchronization structure in the absence of temporal correlation. Thus we consider the simplified log-linear model of (10). We are concerned with two problems: identifying the correlation structure Ξ and estimating the interaction strength vector θ Ξ. Information about p(x ) prior to observing any data is represented by the prior distribution over Ξ and the θ’s. Observations are used to update this probability distribution to obtain a posterior distribution over structures and parameters. The posterior probability that neurons in the set A exhibit an order-|A| interaction is the sum of the posterior probabilities of interaction structures Ξ for which A∈Ξ. In what follows, we confine our discussion to the case of spatial correlations. A heuristic treatment of temporal correlations is discussed in Section 6.1.1, while full treatment of spatiotemporal interactions will appear in a future paper. We estimate both structure and parameters in a unified Bayesian framework. Results include a probability, given the observations, of an order |A| interaction among neurons in A, together with a posterior distribution for the strength of the interaction, conditional on its occurrence. The prior distribution we use is a mixed discrete/continuous distribution. Each structure Ξ is assigned a prior probability. Conditional on structure Ξ, each nonzero θ A is assigned a continuous distribution. The posterior distribution is also a mixed discrete continuous distribution. The posterior distribution for θ A represents information about the magnitude of the interaction. The mean or mode of the posterior distribution can be used as a point estimate of the interaction strength; the standard deviation of the posterior distribution reflects remaining uncertainty about the interaction strength. Computing the posterior probability of a structure Ξ requires integrating θ Ξ out of the joint massdensity function for (Ξ, θ ΞX). There are no closed-form solutions for the required integrals. We use Laplace's method (Tierney & Kadane, 1986; Kass & Raftery, 1995) to estimate the posterior probability of structures. The posterior distribution of θ A given frequency data also cannot be obtained in closed form. We use the mode of the posterior distribution as a point estimate of θ A . The standard deviation of θ A , which indicates how precisely θ A can be estimated from the given data, is estimated using a normal approximation to the posterior distribution. The covariance matrix of the θ A is estimated as the inverse Fisher information matrix evaluated at the mode of the posterior distribution. The posterior probability of an interaction A is the sum over of the posterior probabilities of all structures containing A. The total number of structures is much too large to enumerate explicitly. We used a Markov Chain Monte Carlo Model Composition algorithm (MC3) to search over structures. This is a stochastic algorithm that converges to a stationary distribution in which a structure Ξ is visited with probability equal to its posterior probability. The prior distribution we used has two components. The first component assigns a prior probability to each structure. In our model, interactions are independent of each other and each interaction has a probability of 0.1. This reflects the prior expectation that not many interactions are expected to be present. The second component of the prior distribution is the conditional distribution of interaction strengths given the structure. If an interaction A is absent, the corresponding strength parameter θ A is taken to be identically zero given structure Ξ. All interactions A∈Ξ are taken to have independent and normally distributed interaction strengths with mean zero and standard deviation 2. This reflects the prior expectation that interaction strength magnitudes are rarely larger than 4 in absolute value.11 Using data to infer the distribution involves two subproblems: Given a fixed interaction structure Ξ, infer the parameters θ A for A∈Ξ; and determine the posterior probability of the interaction structure Ξ. These problems are considered separately in the following subsections. These subsections may be omitted by the reader not interested in the technical details. 11 The choice of distribution was informed by experience analyzing other data sets and by discussions with neuroscientists. The symmetry of the normal distribution is unrealistic in that most interaction parameters are expected to be positive. However, the convenience of the normal distribution outweighed this disadvantage. 5.2 Estimating Parameters for an Interaction Structure In this section, we consider the problem of using observations to estimate interaction strengths {θ A}A∈Ξ conditional on a fixed interaction structure Ξ. Initial information about θ A is expressed as a prior probability distribution g(θ|Ξ). Let x 1 ,…,x N be a sample of N independent observations from the distribution p(x|θ,Ξ). The joint probability of the observed set of configurations, p(x1 |θ, Ξ)Lp( xN θ,Ξ) , viewed as a function of θ, is called the likelihood function for θ. From (2), it follows that the likelihood function can be written L(θ) = p(x1 | θ,Ξ)Lp(xN | θ,Ξ) = exp ∑ h(xi | θ) = exp N ∑θ A t A , i A∈Ξ (13) where t ζ = N1 ∑ t ξi is the frequency of simultaneous activation of the nodes in the set A. The expected value of T ζ is the probability that TA=1 and is simply the marginal function for the set A. The observed value t ζ is referred to as the marginal frequency for A. The posterior distribution for θ given the sample x 1 , …, x N is given by g(θ | Ξ, x1 ,…,xN ) = Kp(x 1 | θ,Ξ)Lp(xN | θ, Ξ)g(θ | Ξ) (14) where the constant of proportionality K is chosen so that (4) integrates to 1: K = ∫ p(x1 | θ,Ξ)Lp(x N |θ,Ξ)g(θ | Ξ)dθ' θ' −1 (15) In this expression, θ’ is the vector of θ A for nonempty A∈Ξ. Integration is performed only over parameters that may vary independently. Because the probabilities are constrained to sum to 1, θ ∅ is a function of the other θ A: θ ∅ = − log ∑ exp ∑ θ At A (x ) x A∈Ξ A≠∅ (16) The random vector T of marginal frequencies is called a sufficient statistic for θ because the posterior distribution of θ depends on the data only through T . 12 Another way of expressing the fact that T is a sufficient statistic for θ is that the max-ent model consistent with all marginals is the same distribution that has θ as its effects (Cover & Thomas, 1991). Thus, for the purpose of computing the posterior distribution for a fixed structure, no information is lost if the data are summarized by the vector of observed cluster activation frequencies for those clusters belonging to Ξ. A structure Ξ is specified by enumerating those effects θ A that are nonzero. The prior distribution g(θ|Ξ) expresses prior information about the nonzero θ A. We assume that the nonzero θ A are normally distributed with zero mean and standard deviation σ=2. That is, we are assuming that the θ A are symmetrically distributed about zero (i.e., excitatory and inhibitory interactions are equally _ _ The sufficient statistic T contains TA only for those clusters in Ξ. For notational simplicity the dependence of T on the structure Ξ is suppressed. 12 likely) and that most θ A lie between -4 and 4. The standard deviation σ=2 is based on previous experience applying this class of models (Martignon et al., 1995) to other data. The posterior distribution g(θ|Ξ, x1 ,…, x N ) cannot be obtained in closed form. Thus approximation is necessary. Options for approximating the posterior distribution include analytical or samplingbased methods. Because we must estimate posterior distributions for a large number of structures, Monte Carlo methods are infeasibly slow. We therefore use an analytical approximation method. We approximate g(θ|Ξ, x1 ,…, x N ) as the standard large-sample normal approximation. The approximate posterior mean is given by the mode θ˜ of the posterior distribution. The posterior mode θ˜ can be obtained by using Newton’s method to maximize the logarithm of the joint massdensity function: θ˜ = argmax θ {log ( p(x 1 | θ,Ξ)Lp(xN | θ,Ξ)g(θ | Ξ))} (17) The approximate posterior covariance is equal to the inverse of the Hessian matrix of second derivatives (which can be obtained in closed form): −1 Σ˜ = [ −D 2θ log( p(x1 | θ, Ξ)Lp(x N |θ,Ξ)g(θ | Ξ))] (18) The normal approximation is accurate for large sample sizes (De Groot, 1970). The posterior density function is always unimodal, and we have observed that the conditional density for θ A given the other θ’s is not too asymmetric even when the corresponding marginal TA is small. Nevertheless, the quality of the Laplace approximation is a question worthy of further investigation. 5.3 Estimating the Posterior Probability of Correlations To perform inference with multiple structures, it is natural to assign a prior distribution for θ that is a mixture of distributions of the form (7). That is, a structure probability π Ξ and a prior distribution g(θ|Ξ) is specified for each of the interaction structures under consideration. The structure-specific parameter distribution g(θ|Ξ) was described above in Section 3. To obtain the prior distribution for structures, we used discussions with neuroscientists and experience fitting similar models to other data sets. We expected all θ Α for single element A to be nonzero. The prior distribution we used assumed that the θ A were zero or nonzero independently, and each θ A with |A|>1 had prior probability of .1 of being nonzero. The results of the analysis were insensitive to the (nonzero) prior probability of including singleton A. The posterior distribution of θ given a sample of observations is also a mixture distribution: g(θ|x 1 ,…,x N) = ∑ π * g(θ | Ξ, x ,…, x Ξ Ξ 1 N ) (19) where π *Ξ is the posterior probability of structure Ξ and g(θ |Ξ, x1 ,…, xN ) is the posterior distribution of θ given structure Ξ as defined in (4) and (5). The ratio of posterior probabilities for two structures Ξ1 and Ξ2 is given by p(Ξ1 | x1 ,K ,xN ) p(x1 ,K, x N | Ξ 1 ) π Ξ 1 π*Ξ 1 = = p(Ξ 2 | x1 ,K ,x N ) p(x 1,K, x N |Ξ 2 ) π Ξ2 π* (20) Ξ2 Thus, the posterior odds ratio is obtained by multiplying the prior odds ratio by the ratio of marginal probabilities of the observations under each of the two structures. This ratio of marginal probabilities is called the Bayes factor (Kass & Raftery, 1995). The marginal probability of the observations under structure Ξ is obtained by integrating θ’ out of the joint conditional density: p(x 1,K.x N |Ξ) = ∫ p(x 1 | θ', Ξ)Lp(xN | θ', Ξ)g(θ'| Ξ)dθ' (21) We assumed in Section 3 that the joint mass-density function (and hence the posterior density function for θ) was highly peaked about its maximum and approximately normally distributed. The marginal probabilit y p(x1 ,K. x N |Ξ) is approximated by integrating this normal density: p˜ (x 1,K.x N |Ξ) ≈ (2π)d /2 Σ ˜ 1 / 2 p(x | θ˜ ,Ξ)Lp(x | θ˜,Ξ)g(θ˜ | Ξ) 1 N (22) This approximation (12) is known as Laplace’s approximation (Kass & Raftery, 1995; Tierney & Kadane, 1986). The posterior expected value of θ is a weighted average of the conditional posterior expected values. As noted above, these expected values are not available in closed form. Using the conditional MAP (=maximum a posteriori) estimate θ˜ Ξ to approximate the conditional posterior expected value, we obtain the point estimate θ˜ = ∑ π *θ˜ Ξ Ξ Ξ (23) In (23), the value θ˜ A =0 is used for structures not containing A. Also of interest is an estimate of the value of θ A given that θ A≠0, which is obtained by dividing θ˜ A by the sum of the π Ξ for which A∈Ξ. Equation (18) can be used to approximate the posterior covariance matrix Σ˜ Ξ for θ conditional on structure Ξ. Again, the unconditional covariance can be approximated by a weighted average: Σ˜ = ∑ π * Σ˜ Ξ Ξ (24) Ξ Computing the posterior distribution requires computing, for each possible structure Ξ, the posterior probability of Ξ and the conditional distribution of θ given Ξ. This is clearly infeasible: k For k nodes there are 2k activation clusters, and therefore 2 2 possible structures. It is therefore necessary to approximate (19) by sampling a subset of structures. We used a MC3 algorithm (Madigan & York, 1993) to sample structures. A Markov chain on structures was constructed such that it converges to an equilibrium distribution in which the probability of being at structure Ξ is equal to the Laplace approximation to the structure posterior probability π *Ξ . We used a MetropolisHastings sampling scheme, defined as follows: When the process is at structure Ξ, a new structure Ξ’ is sampled by either adding or deleting a single cluster. The cluster A’ to add or delete is chosen by a probability distribution ρ(A’|Ξ). 13 The selected cluster A’ is then either accepted or rejected, with the probability of acceptance given by p(x 1,K.x N | Ξ' )π Ξ' ρ(A'| Ξ) min 1, p(x1 ,K.x N | Ξ)π Ξ ρ(A' |Ξ') (25) We ran the MC3 algorithm for 15,000 runs. We estimated the posterior probability of a structure as its frequency of occurrence over the 15,000 runs. We estimated interaction strength parameters and To improve acceptance probabilities, we modified the distribution ρ(A’|Ξ) as sampling progressed. The sampling probabilities were bounded away from zero to ensure convergence. 13 standard deviations using only the 100 highest probability structures. Although the number of possible structures is astronomical, the vast majority of structures have extremely small probabilities. The practice of using the best 100 models to estimate interaction strengths is justified first because estimates based on the best 100 models of the interaction probabilities were very similar to those based on sampling frequencies, and second because the between-structure variance components for the interaction strengths were generally very small (the only exceptions being lowprobability interactions that were highly correlated with other interactions). 5.4 A heuristic for detecting temporal patterns The correct way for modelling temporal structure is the Markov chain defined in (9). But the amount of data required to estimate this Markov Chain for reasonable time delays (say, 50 to 100 ms) is enormous and so is the time required for any statistical approach to this estimation task. We propose a heuristic than can be useful as an approximation. We see a temporal pattern as a “shifted synchrony”. Suppose we observe neuron 1 fires exactly two bins after neuron 2 quite often. When do we declare that that this phenomenon is significant? In our simplified approach we shift the data of neuron 2 two bins ahead of neuron 1 and, neglecting the two first bins of neuron 1 and the last two of neuron 2, we have an artificially created parallel process for these two neurons such that the temporal pattern has now become a synchrony. We will declare that a temporal pattern is significant if the synchrony obtained by performing the corresponding shifts is significant. We introduce some notation: Given four neurons 1,2,3,4, we use the notation 12[1]3[2]4[-2] to indicate that we shift neuron 2 one bin after neuron 1, neuron 3 two bins after neuron 1, and neuron 4 two neurons before neuron 1. The first number from left to right indicates the neuron with respect to which all shifts have been performed. Interaction Strenght -65 -36 -29 -25 -21 -18 -15 -12 -9 -6 -3 0 3 6 9 12 15 Figure 3: Histogram of Estimated Interactions of Two Neurons (1,2 of Table 5) 6 Applying the Model to Simulated Data We applied our models to synthetically generated data. We generated data randomly from a model of the form (2), where we specified Ξ and θ A. Table 1 shows the nonzero θ A in the model we used. 18 Cluster A θA 4,6 0.45 3,4,6 0.74 2,3,4,5 1.79 2,3,4,5,6 0.61 Table 1: Nonzero Parameter Values for Synthetic Data We used the θ A from Table 1 to compute p(x) from (2) and generated random observations from p(x). Results from the analysis of a sample of 10,000 randomly generated data appear in Table 2. Cluster A G2 Posterior Probability of A (Frequency) Posterior Probability of A (Best 100 models) MAP estimate θ˜ ξ Standard Deviation of θA 4,6 0.0001 0.99 0.99 0.46 0.10 3,4,6 <0.01 0.93 0.96 1.13 0.26 Table 2: Results for a randomly generated sample of 10.000 data from the distribution specified in Table 1 We ran the MC3 search algorithm described in Section 4 for 15,000 iterations. Posterior probabilities, estimated θ A, and estimated σA are shown in Tables 1 and 2 for all interactions A with estimated posterior probability of at least .1 (i.e., interactions for which the posterior probability is at least as large as the prior probability). Posterior probabilities for interactions were estimated in two different ways: by frequencies collected over the 15,000 iterations of the MC3 algorithm and by normalizing probabilities for the 100 highest probability structures enumerated during the model search. Also shown in Table 2 are estimates for the interaction strength parameters θ A conditional on θ A≠0. The estimate θ˜ A is a weighted average of the MAP estimates (7). Structures included in the weighted average were those from the 100 most probable models that contain θ A. Structure weights are proportional to the structure posterior probability. The estimate σ˜ A is obtained from the sum of ”within” and ”between” variance components: ( ) 2 2 σ˜ 2A = ∑ p˜Ξ σ˜ AΞ + θ˜ AΞ − θ˜ A A∈Ξ (26) The sum is over the 100 most probable enumerated structures that include A; the weight p˜ Ξ is proportional to the posterior probability of Ξ and normalized to sum to 1; the within-structure variance component is a weighted average of the appropriate diagonal elements of (18); and the between-structure variance component is the sum of squared deviations of the structure-specific parameter estimates about their mean. The results shown in Table 1 and Table 2 indicate that these two methods yield similar estimates. In Table 2 the (4,6) and (3,4,6) interactions exhibit a very high posterior probability. The former was estimated quite precisely, the latter to within two posterior standard deviations. Neither the (2,3,4,5) nor the (2,3,4,5,6) interaction was detected by the frequentist/Bayesian analysis of the synthetic data (their posterior probabilities were .03 and .04, respectively). This suggests that the magnitude of these interactions was not sufficient to be detected in a sample of this size. No interactions that were not present in the synthetic data model were detected by the data analysis. 6.1 Neuronal Interactions in Experimental Data We begin by presenting data obtained by Vaadia: In the experiment spiking events among groups of neurons were analyzed through simultaneous recordings of 6 neurons in the cortex of Rhesus monkeys. The monkeys were trained to localize a source of light and, after a delay, to touch the target from which the light was presented. At the beginning of each trial the monkeys touched a "ready-key", then a central red light was turned on (ready signal). Three to six seconds later, a visual cue was given in the form of a 200-ms light blink coming from either the left or the right. After a delay of 1 to 32 seconds, the color of the ready signal changed from red to yellow and the monkeys had to release the ready key and touch the target from which the cue was given. The spikes of each neuron were encoded as discrete events by a sequence of zeros and ones with time resolution of 1 millisecond. The activity of the whole group was described as a sequence of configurations or vectors of these binary states. Since the method presented in this paper for detecting synchronizations does not take into account nonstationarities, the data were selected by cutting segments of time during which the cells did not show significant modulations of their fiiring rate. The segments were taken from 1000 ms before the cue onset till 1000 ms thereafter. The duration of each segment was 2 seconds. We used 94 such segments (total time - 188 seconds) for the analysis presented below. The data were then binned in time windows of 40 milliseconds. The choice of the bin length was determined in discussion with the experimenter. The frequencies of configurations of zeros and ones in these windows are the data used for analysis in this paper. We analyzed recordings prior to the ready signal separately from data recorded after the ready-signal. Each of these data sets is assumed to consist of independent trials from a model of the form (2). Tables 3 and 4 present the same type of results as those of Table 2 in the previous section. Gt Cluster A Posterior Probability Posterior of A Probability of A (Frequencies) (Best 100 models) MAP estimate θ˜ A Standard Deviation of θ A 4,6 .001 0.98 1.00 0.49 0.11 2,3,4,5 >.09 0.33 0.36 2.34 0.67 3,4,6 >.05 0.22 0.15 0.80 0.27 2,3,4,5,6 >.05 0.16 0.13 2.53 0.88 1,4,5,6 >.05 0.16 0.10 6.67 1.19 3,4 >.05 0.12 0.08 0.63 0.23 Table 3: Results for Pre-Ready Signal Data, Coefficients with Posterior Probability > 0.1 There was a high probability second-order interaction in each data set: (4,6) in the pre-ready data and (3,4) in the post-ready data. In the pre-ready data, a fourth-order interaction (2,3,4,5) had posterior probability about 1/3 (this represents approximately three times the prior probability of .1). The tables show a few other interactions with posterior probability larger than their prior probability. Posterior Posterior MAP estimate θ˜ ξ Probability of A Probability of A (Frequency) (Best 100 models) Cluster A G2 3,4 0.03 0.86 0.94 1.00 0.27 2,5 >0.05 0.25 0.18 0.98 0.34 1,4,5,6 >0.05 0.18 0.13 1.06 0.36 1,4,6 >0.05 0.15 0.08 0.38 0.13 Standard Deviation of θ A Table 4: Results for Post-Ready Signal Data: Effects with Posterior Probability > 0.1 Several data sets from this type of experiment were analyzed under the guidance of the sixth author, who conducted the experiments. With only one exception interactions of order 2 or more were all characterized by positive effects. In data sets of 6-8 neurons from different segments on the experimental data described above the presence of triplets was rare. Comparison of Tables 3 and 4 reveals some similarities and some important differences. The preready data shows strong evidence for the (4,6) interaction; there is no evidence for this interaction in the post-ready data. The post-ready data shows strong evidence for the (3,4) interaction; there is no evidence for this interaction in the pre-ready data. (Although the (3,4) interaction term appears in Table 3, its posterior probability is barely greater than its prior probability, indicating that the data show evidence neither for its presence nor for its absence.) Both these second-order interactions are positive. Single-element effect values are negative because the overall level of activation in these recordings was low. Results of this type, that is, of varying second-order structure with varying attentional state, have been obtained previously by several groups of researchers (Grün, 1995; Riehle et al., 1998) who have used the method introduced by Palm et al. (1989) for detecting surprising correlations. This method is essentially consistent with the method presented here for the second-order case (a difference of the two approaches is the test used for determining significance: We use G2 while Palm et al. (1988) use a Fisher significance test comparing the data with the binomial distribution determined by the success probabilities fixed by the first-order model.) To double-check of our methods the fifth author also provided data from biologically plausible simulations of neural activity. Only second-order interactions of a different type were simulated, both synchronous and with small time delays. Both the frequentist and the Bayesian methods detected the simulated interactions and, in the case of overlapping couples, did not misdetect nonexisting triplets. 6.2 Neuronal Interactions in Anesthetized Rat Somatosensory Cortex We also applied the models to data collected from the vibrissal region of the rat cortex. The vibrissae are arranged in five rows on the snout (named A, B, C, D, and E) with four to seven vibrissae in each row (Figure 4A). Neurons in the vibrissal area of the somatosensory cortex are organized into columns (Figure 4B); layer IV of the column is composed of a tightly packed cluster of neurons called a ”barrel” (Woolsey and Van der Loos, 1970). Each barrel-column is topologically related to a single mystacial vibrissa on the contralateral snout; thus ”vibrissa D2” (second whisker in row D) is linked to ”column D2” (Welker, 1971), our wish was to find out whether interacting neurons are distributed across cortical columns or restricted to single columns. furthermore we examined whether the spatial distribution of interacting neurons varies as a function of the stimulus site. The data analyzed here were recorded from the cortex of a rat lightly anesthetized with urethane (1.5 g/kg) and held in a stereotaxic apparatus. Cortical neuronal activity was recorded through an array of six tungsten microelectrodes inserted in cortical columns D1, D2, D3, C3, as well as in the ”septum” located between columns D1 and D2 (Figure 4). Using spike sorting methods, events from a total of 15 separate neurons were discriminated. Locations of the neurons are shown in Figure 4. During the recording session, individual whiskers were deflected across 50-55 trials by a computer-controlled piezoelectric wafer that delivered an up-down movement lasting 100 ms; the stimulus was repeated once per second (Diamond et al, 1993). We have restricted the analysis to data collected during stimulation of vibrissae D1, D2, and D3 and only during the 200 ms peristimulus period (100 ms after the up movement and 100 ms after the down movement). For each stimulus site, then, there were 10,000-11,000 ms of data. As in the previous section, the spiking events (in the 1 ms range) of each neuron were encoded as a sequence of zeros and ones, and the activity of the whole group was described as a sequence of configurations or vectors of these binary states. The interactions illustrated in Figure 4 are those for which the likelihood test statistic is significant at the 0.0001 level. Figure 4A shows the interactions occurring during stimulation of whisker D1. Two neurons within column D1 showed a significant negative correlation. Interactions during stimulation of whisker D2 are given in Figure 4B. One neuron in column D3 and one in column C3 showed a pairwise positive interaction (firing together less frequently than expected by chance). In addition, a positive higher order interaction emerged, consisting of three neurons distributed across the D1-D2 septum and columns D2 and D3. During stimulation of whisker D3 a pairwise and a higher order interaction were detected, both of them negative (Figure 4C). positive correlation negative correlation A D1 1 2 septum 3 4 D2 5 6 D3 7 9 12 8 10 13 11 C3 D1 stimulation 14 15 B D1 1 2 septum 3 4 D2 5 6 D3 7 9 12 8 10 13 11 C3 D2 stimulation 14 15 C D1 1 2 septum 3 4 D2 5 6 D3 7 9 12 8 10 13 11 C3 D3 stimulation 14 15 Figure 4: Selected Interactions (G2<0.0001) from Results of the Analysis of Data on Spike Trains from the Somatosensory Cortex of Rats From analysis of this limited data set, several interesting observations can be made: (1) Both positive and negative interactions were detected; (2) interactions occurred both within a cortical columnar unit and across columns; (3) interactions were stimulus dependent (neurons were not continuously correlated with one another but became grouped together as a function of the stimulus parameter); (4) during different stimulus conditions a single neuron may take part in different groups (neuron 10 during stimulation of whisker D2 and D3); (5) during one stimulus condition, the same neuron can participate in two separate interactions (neuron 10 during stimulation of whisker D3). 6.3 Higher order synchronization in the visual cortex of the behaving macaque Precise patterns of neural activity of groups of neurons in the visual cortex of behaving macaques was detected by means of the analysis of data on multi-unit recordings obtained by Freiwald. The experiment consisted of a simple fixation task: the monkey was supposed to learn to detect a change in the intensity of a fixated light point on a screen and react with a motoric answer. The fixation task paradigm is the following: A fixation point appears on the screen and stays on the screen for 8 to 9 seconds. The monkey fixates this point and then presses a bar. After the bar is pressed an interval of approximately five to six seconds begins, during which the monkey fixates the point and maintains the bar pressed. Afterwards, the point darkens and disappears from the screen, and, as a consequence, the monkey releases the bar. During the five to six seconds a visual stimulus is presented on the screen, which is not relevant for behavior. The data presented here were from four neurons recorded in the inferotemporal cortex (IT) on repeated trials of 5.975 ms each, including 1000 ms before the stimulus onset. We decomposed each trial into a first chunk of 1.000 ms, considered stationary (pre-stimulus), a non-stationary interval of 800 ms (phasic response), and then four segments of 1.000 ms each (tonic response), followed by a short last segment of 175 ms. We chose a bin width of 5 ms. We chose to here present a comparison between the activity during the first 1000 ms before the stimulus onset and the 1000 ms right after the non-stationary interval corresponding containing the phasic response. We performed a synchronization analysis both with the frequentist and the Bayesian method and obtained compatible results, in the sense that all synchronizations detected by the Bayesian method were declared significant at the .001 level. Cluster A Posterior Probability of A (Frequency) Posterior Probability MAP estimate θ˜ ξ of A (Best 100 models) Standard Deviation of θ A Fixation (1-1000 ms) 3,4 0.99 1.00 0.69 0.08 2,4 1.00 1.00 0.56 0.04 2,3 1.00 1.00 1.54 0.05 2,3,4 0.22 0.22 -0.66 0.02 1,4 0.99 1.00 0.70 0.01 1,3 0.99 1.00 1.72 0.01 1,2 0.99 1.00 1.45 0.00 1,2,3 0.99 1.00 -1.26 0.03 Table 5: Synchronies with probability larger than 0.1 in the first 1000 ms in the fixation task Cluster A Posterior Probability of A (Frequency) Posterior Probability MAP estimate θ˜ ξ of A (Best 100 models) Standard Deviation of θ A Phase 1 (1800 - 2800 ms) 3,4 0.26 0.26 0.29 0.30 2,4 1.00 1.00 0.53 0.02 2,3 0.99 1.00 1.06 0.05 2,3,4 0.17 0.16 -0.07 0.07 1,4 0.71 0.70 0.32 0.01 1,3 1.00 1.00 1.14 0.04 1,2 1.00 1.00 0.88 0.01 1,2,3 0.78 0.78 0.13 0.02 Table 6: Synchronies with probability larger than 0.1 in the first 1000 ms after the visual stimulus. 7 Discussion This paper proposes a parameterization of synchronization and, in general, of temporal correlation of neural activation of more than two neurons. This parameterization has a sound informationtheoretical justification. If the problem is to analyze a group of neurons and establish whether they fire in synchrony, the statistical problems of estimating the significance of the corresponding effect being nonzero has a straightforward, reliable treatment. If the problem is to detect the whole interaction structure in a group of neurons (i.e., which subsets have interactions and how strong) the Bayesian approach has advantages over the frequentist approach because it does not have to face the problem of multiple null hypotheses and the multiple significance levels associated with them. Yet the Bayesian approach is of astronomical complexity when the temporal interaction structure of, say, 8 neurons is to be assessed. Even the heuristic method briefly discussed in section 6.1.1. becomes basically infeasible for the Bayesian approach we exposed here, at least in its present form. New techniques for speeding up Bayesian search across structures will be presented in a forthcoming paper. An important underlying assumption in our investigations has been that the data are basically stationary. This is seldom the case. As we know from the important work by Abeles, Bergman, Gat, Meilijson, Seidenmann, Tishby, and Vaadia (1995), cortical activity flips from one quasistationary state to the next. These authors developed a hidden Markov model technique to determine these flips. A combination of their methods with the ones presented here would allow the analysis of structure changes through quasi-stationary segments. Another advancement in global structure analysis of spike activity has been obtained by de Sa’, de Charms, and Merzenich (1997) by means of a Helmholtz machine that determines highly probable patterns of activation based on spike train data. Here again a combination of methods would allow analysis of the correlation structure in probable patterns. While the first techniques for analysis of patterns in neural activation of recorded cells were simple and transparent, the new techniques for determining correlation structure of more than two neurons are complex and often even infeasible. The reason for our presentation of both the frequentist and the Bayesian approach to detecting correlation structure is our wish to reinforce the use of the frequentist method, in spite of all its shortcomings, because it is quick and can be used for large numbers of neurons and long time delays. Our experience with the systematic comparison of the two methods has enhanced the confidence that a careful frequentist strategy is fairly reliable. 8 Acknowledgments The authors thank Günther Palm for helpful discussions. An anonymous reviewer of an earlier version of this paper is gratefully acknowledged for extremely useful comments that have influenced the preparation of this paper. Dr. Laskey’s work was supported by a Career Development Fellowship with the Krasnow Institute for the study of cognitive science at George Mason University. References Abeles, M. (1991). Corticonics: Neural Circuits of the Cerebral Cortex. Cambridge: Cambridge University Press. Abeles, M., Bergman, H., Gat, I., Meilijson, I., Seidenmann, E., Tishby, N. and Vaadia, E. (1995). Cortical Activity Flips among quasi-Stationary States. Proc. Natl. Acad. Sci. 92: 8616-8620. Abeles, M., Bergman, H., Margalit, E. and Vaadia, E. (1993). ”Spatiotemporal Firing Patterns in the Frontal Cortex of Behaving Monkeys.” Journal of Neurophysiology 70, 4: 16291638. Abeles, M. and Gerstein, G. (1998). Detecting Spatiotemporal Firing Patterns among Simultaneously Recorded Single Neurons. J. Neurophysiol. 60: 909-924. Abeles, M., Prut, Y., Bergman, H. and Vaadia, E. (1994). Synchronization in Neural Transmission and its Importance for Information Processing. Prog. Brain. res. 102: 395-404. Aertsen, A., Gerstein, G., Habib, M. and Palm, G.(1989). Dynamics of Neural Firing Correlation: Modulation of ”Effective Connectivity.”. J. Neurophysiol.. 61: 900-917. Aertsen, A. (1992) Detecting Ttriple Activity. Preprint. Bishop, Y., Fienberg, S. and Holland, P. (1975) Discrete Multivariate Analysis. Cambridge, MA: MIT Press. Cover, T. and Thomas, J. (1991). Elements of Information Theory. New York: Wiley Series in Communications. de Finetti, B. (1937). La prevision; ses lois logiques, ses sources subjectives. Annales de l’ Institut Henri Poincare. 7: 1-68. (Reprinted in 1964 in English translation as ”Foresight: its Logical Laws, its Subjective Sources”, in Studies in Subjective Probability, edited by Kyburg, Jr., H. E., and Smokler, H. E.). de Sa’, R., de Charms, R. and Merzenich, M. (1997). Using Helmholtz Machines to Analyze Multi-Channel Neuronal Recordings. Neural Information Processing System. 10: 131-136. De Groot, M. (1970). Optimal Statistical Decisions. New York: McGraw-Hill. Diamond, M., Armstrong-James, M. and Ebner, F. (1993). Experience-Dependent Plasticity in the Barrel Cortex of Adult Rats, Proc. Natl. Acad. Sci. 90: 2602-2606. Gerstein, G., Perkel, D. and Dayhoff, J. (1985). Cooperative Firing Activity in Simultaneously Recorded Populations of Neurons: Detection and Measurement. Journal of Neuroscience, 5: 881-889. Good, I. (1963). On the Population Frequencies of Species and the Estimation of Population Parameters. Biometrika. 40: 237-264, Grün, S., Aertsen, A., Vaadia, E. and Riehle, A. (1995). Behavior-Related Unitary Events in Cortical Activity. Learning and Memory: 23rd Göttingen Neurobiology Conference (poster presentation). Grün, S. (1996). Unitary Joint-Events in Multiple-Neuron Spiking Activity-Detection, Significance and Interpretation. Frankfurt : Verlag Harry Deutsch. Hebb, D. (1949). The Organization of Behavior. New York: Wiley. Kass, R. and Raftery, A. (1995). Bayes Factors. Journal of the American Statistical Association. 90, no. 430: 773-795. Laskey, K. and Martignon, L. (1996). Bayesian Learning of Log-linear Models for Neural Connectivity. Proceedings of the XII Conference on Uncertainty in Artificial Intelligence. San Mateo: Horwitz, E. ed., Morgan-Kaufmann. Madigan, D. and York, J. (1993). Bayesian Graphical Models for Discrete Data. Technical Report 239, Department of Statistics, University of Washington. Martignon, L., v. Hasseln, H., Grün, S., Aertsen, A. and Palm, G. (1995). Detecting Higher Order Interactions among the Spiking Events of a Group of Neurons” Biol.Cyb. 73, 6981. von Mises, R. (1939). Probability, Statistics and Truth. London: George Allen & Unwin Ltd. Neyman, J. and Pearson, E. (1928). On the Use and the Interpretation of Certain Test Criteria for Purposes of Statistical Inference, BiometriKa, 20: 175-240, part I: 263-94 part II. Palm, G., Aertsen, A. and Gerstein, G. (1988). On the Significance of Correlations among Neuronal Spike Trains. Biol. Cybern. 59: 1-11. Prut, Y., Vaadia, E., Abeles, M., Haalman, I. and Slovin, H. (1993). Dynamics of Neuronal Interaction in the Frontal Cortex of Behaving Monkeys. Concepts in Neuroscience , 4, no 2: 131-158. Prut, Y., Vaadia, E., Bergman, H., Haalman, I., Slovin, H. and Abeles, M. (1998). Spatiotemporal Structure of Cortical Activity: Properties and Behavioral Relevance. Journal of Neurophysiology. 79: 2857-2874. Rauschecker, J. (1991) Mechanisms of Visual Plasticity: Hebb Synapses, NMDA Reception and beyond. Phys. Rev.. 71: 587-615. Riehle, A., Grün, S., Diesmann, M. and Aertsen, A. (1998). Science. 281: 34-42. Singer, W. (1994). Time as Coding Space in Neocortical Processing: A Hypothesis. in: Temporal Coding in the Brain. Berlin Heidelberg: Buzsaki, G. et al. (Eds). Springer Verlag. Strangman, G. (1997) Detecting Synchronous Cell Assemblies with Limited Data and Overlapping Assemblies . Neural Computation. 9, 1: 51-76 Tierney, L. and Kadane, J. (1986). Accurate Approximations of Posterior Moments and Marginal Densities. Journal of the American Statistical Association. 81: 82-86. Welker, C. (1971). Microelectrode Delineation of Fine Grain Somatotopic Organization of SmI Cerebral Neocortex in Albino Rat. Brain Res. 26: 259-275 Whittaker, J. (1989). Graphical Models in Applied Multivariate Statistics. New York: Wiley Woolsey, T.A. and Van der Loos, H. (1970). The Structural Organization of Layer IV in the Somatosensory region, SI, of Mouse Cerebral Cortex. Brain Res.. 17: 205-242.