Download Session Slides/Handout

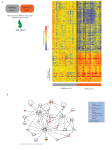
Biostatistics in Practice
Session 6: Case Study
Peter D. Christenson
Biostatistician
http://gcrc.LABioMed.org/Biostat
Case Study
A compound found in red grapes improves the
health and lifespan of mice on a high calorie diet.
Treatment Groups
Male middle-aged mice (11 months) were randomized to:
1. Standard Diet (SD): known as AIN-93G
N=60; N=5 for gene expression
2. High Calorie (HC): SD + coconut oil → 60% fat.
N=55; N=5 for gene expression
3. Resveritrol (HCR): HC + 22.4 mg resveritrol/ kg/day.
N=55; N=4 for gene expression (+1 w/ degraded sample)
Outcome: Mortality
0.42 died
0.58 died
• Methods: Survival Analysis; we have not discussed.
• Similar to mortality ratio for HCR/HC = 0.42/0.58=0.72,
which is a 28% reduction at 114 weeks.
Paper reports a similar “hazard ratio” of 0.69, with a pvalue of 0.02. In general terms, how did they get this?
Outcome: Agility
What statistical analysis was done here?
Outcome: Clinical Markers
What statistical analyses?
Do you agree?
Other Outcomes
Gene Expression in Liver at age 18 months
Fourteen Microarray “Experiments”: each of 5+5+4 mice
had a separate array run for ~40,000 genes.
Gene Expression Data: 536,872 Numbers
38,348 rows:
each a gene
First 2 SD mice.
http://www.grc.nia.nih.gov/branches/
12 others →
rrb/dna/index/dnapubs.htm#2
Gene Expression Results
HCR overexpressed,
compared to
HC.
How do you think
they got these
results for (a) and
(b)?
HCR underexpressed,
compared to
HC.
Microarray Analysis
• How can we analyze these data?
• What are “experimental units”: mice or genes?
• Consider each gene independently?
• If so, Ns of 4 and 5 seem small to say much - low power.
• So, maybe combine genes for larger Ns?
• Pair up HCR and HC mice, find ratio, and average?
• Ratio of mean for N=4 HCR and mean for N=5 HC?
• If p<0.05 is used for each gene, expect many false
positives among 38,348 genes.
• SD among only 5 mice could be large just due to
differences from array to array, not biologic diff,
and thus miss finding important genes.
We will try various analyses with the data in class
Detectable Effects with N=5 per Group
Suppose we
compare the mean
of 5 appropriately
scaled #s for a
gene’s expression
with the mean of 5
in another group,
using a t-test.
SD=√sigma2
So, we need ~ 2SD difference in gene expression to be
fairly sure (80%) of detecting this gene with only N=5+5.
This is a large effect – see next slide.
Detectable Effects with N=5 per Group
Relative Frequency
2SD Shift
Effect
Gene Expression
HC
HCR
Normal
Range
2SD Effect corresponds to 50th → 97th percentile,
about 2/5 of normal range
Detectable Effects with N=5 per Group
So, how can we try to avoid missing genes that are
important, but are not detected with p<0.05?
Recall that p<0.05 corresponds to approximately:
|t| =|effect/SE(effect)| = |Δ/SE(Δ)| = |signal/noise| >2
where noise is a function of ~ SD/ sqrt(N).
Thus, if ↑ N is not possible to reduce noise, we can:
1. Try to reduce SD, or
2. Ignore SD and base the decision for gene selection
on the signal, i.e., effect, i.e., mean differential
expression, only.
Microarray Analysis: 1. Try to reduce SD
Here, SD is the SD among the expressions for 5 mice in a
group.
How can we “reduce SD”? Isn’t it natural subject-tosubject heterogeneity, a characteristic of the population?
This SD is among measured expression, which includes
both array-to-array error and subject-to-subject
heterogeneity. (Confounded-there is no internal control.)
We try to statistically remove some of the inherent arrayto-array error through normalization.
Side Point on Microarray Design
1. Single Channel Chip: 1 sample, many probes.
•
No replicated measures. This study.
2. Two Channel Chip: 2 samples, possibly fewer
probes that are common for both samples.
• One sample may be an internal control.
• The two samples may be matched, e.g.,
• Two conditions, times, or cell types, for
the same subject.
• Twins, littermates, etc, treated differently.
Normalization
There are many ways to normalize. They exploit the
assumption that most of 1000s of genes will be the
same in many subjects. Two common methods:
• Global: All genes in an array are multiplied by the
ratio of the (global) mean over all genes for all
arrays to the mean over all genes for this array.
E.g., array1 has mean 1000 and fourteen arrays
have mean 900, multiply by 0.90.
• Z-score: Replace expression x by z=(x-mean)/SD,
where mean and SD are over genes for this array.
Expression becomes # of SDs deviant from gene
mean.
Microarray Analysis: 2. Ignore SD
Here, SD is the SD among the expressions for 5 mice in
a group.
Use an effect measure for each gene, such as the ratio
of mean of 4 HCR to the mean of 5 HC, usually
standardized to a “normal range” as with z-scores.
Usually select genes with either:
1. Ratio>c or <1/c, some c such as 1.5 or 2.
2. A specified number or percent of genes with
largest or smallest ratios.
Microarray Analysis: This study
Genes selected with both:
1. “Z-Ratio” >1.5 or <-1.5.
2. The p-value from a z-test for comparing the
mean z-score of 4 HCR mice to the mean of 5
HC mice is <0.05.
Raw expression is normalized within each array by
z-scores on log(expression).
The Z-Ratio is the difference between the mean zscore of 4 HCR mice to the mean of 5 HC mice
(which is the numerator for the z-test), divided by
the SD of these differences over different genes.
Microarray Analysis: Gene Hsd3b5
Use raw data
to generate
results for the
most upregulated
gene.
Microarray Analysis: Gene Hsd3b5
Raw
13145.2
14405.2
22271.5
12349.9
14037.6
Log
9.483811
9.575347
10.01106
9.421401
9.549494
Mean
6.54116
6.51822
6.50518
6.41534
6.70083
SD
1.4847
1.5039
1.5105
1.4934
1.5341
261.143
341.867
329.622
368.763
418.856
5.565067
5.834423
5.797947
5.910154
6.037528
6.66922
6.72307
6.68663
6.58712
6.7602
1.5141
1.5464
1.5291
1.4414
1.5719
ZscoreGroup
1.967 SD
2.02 SD
2.303 SD
1.997 SD
1.843 SD
-0.72
-0.57
-0.57
-0.47
-0.45
9663.86 9.176149 6.65757 1.526 1.639
8397.5 9.03569 6.56456 1.5104 1.623
3243.64 8.084451 6.61664 1.4968 0.976
1226.37 7.111811 6.67217 1.443 0.305
HC
HC
HC
HC
HC
HCR
HCR
HCR
HCR
Microarray Analysis: Gene Hsd3b5
Two Sample T-Test for HCR vs. HC on Gene Hsd3b5
N
Mean
SD
SE
HCR
4
1.136
0.634
0.32
HC
5
-0.555
0.107
0.048
Diff
1.691
95% CI for Diff: ( 1.02,
T-Test T = 5.96
2.362)
P = 0.0006
Antilog(1.691) =~ 5.42 fold greater HCR expression
“Z-Score” = Diff of logs/SD = 1.691/0.14 = 11.99
Here, SD=0.14 is among these diffs over genes.
Expected Identified Genes among
38,348 Genes using p-values
Suppose the decision rule is to declare a particular gene
important if its mean expression in HCR mice differs
enough from that for HC mice so that p<0.05:
Significantly less → down-regulated.
Significantly more → up-regulated.
Then the expected number of identified genes among,
say, 38,000 that are not affected (false positives) is:
0.05*38,000 = 1900
Thus, confirmatory analyses such as PCR are needed.