Download Jan 7, 2015. PASSIVE ELECTRICAL PROPERTIES OF MEMBRANES

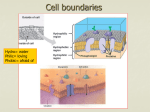
Cellular Neuroscience (207)
Ian Parker
Lecture # 2 - Passive electrical
properties of membranes
(What does all this electronics stuff mean for a neuron?)
http://parkerlab.bio.uci.edu
Membrane structure
Fatty acid tail
polar head
Permeation across the lipid bilayer increases with increasing lipid solubility.
Ions and water are almost completely impermeant – protein channels and carriers.
Provide pathways for selective movement of ions and molecules across the membrane.
The cell membrane (lipid bilayer) acts as a very good insulator, but has high capacitance.
(WHY?)
Specific membrane resistance
1 cm
Resistance of 1 cm2 of membrane (Rm)
Rm of a lipid bilayer >106 W cm2
But membrane channels can greatly increase the
membrane conductance
Specific membrane capacitance
extracellular fluid
membrane
intracellular fluid
The insulating cell membrane (dielectric) separates two good conductors (the fluids
outside and inside the cell), thus forming a capacitor.
Because the membrane is so thin (ca. 7.5 nm), the membrane acts as a very good
capacitor.
Specific capacitance (capacitance of 1 cm2 of membrane : Cm)
Cm ~ 1 mF cm-2 for cell membranes
Input resistance of a cell
Record voltage (V)
Inject current (I)
cell
Input resistance Rin = V/I
Rin decreases with increasing size of cell (increasing membrane area)
Rin increases with increasing specific membrane resistance
[If I = 10 nA and V = 5 mV, what is Rm ???]
A neuron as an RC circuit
Record voltage (V)
Inject current (I)
I
cell
V
Cm
Rm
E
inside
tim e
outside
Voltage changes exponentially
with time constant tm
tm = Rm * Cm
So tm will be longer if Rm is high
“ “ “ “
“ and if Cm is high
We can directly measure Rm and tm
so we can calculate Cm = tm / Rm
Given that Cm ~ 1 mF cm2, we can then calculate the
membrane area of the cell
EXERCISE
From example trace given in class;
Measure time constant
Measure change in membrane potential resulting from a given injection of current
Calculate input resistance
Calculate total capacitance of cell membrane
Estimate diameter of the cell
But, neurons are not usually spheres!
What about axons and dendrites?
For a spherical cell, all regions on the cell membrane are at
the same potential as each other (isopotential). This is not the
case for long, thin processes such as axons and dendrites.
The voltage change induced by a ‘square’ pulse of injected current gets smaller
and more rounded with increasing distance along an axon
Space constant
Space constant (l) is the distance at which the change in membrane potential (D Vm)
falls to 1/e of some initial value.
(What is the space constant in the example above?)
Equivalent circuit of an axon
The math for this gets complicated …
So, we will just consider a simple case where the duration of current injection is
long enough for the membrane capacitance to fully charge. Then;
(Qualitatively, how would the space constant be affected if the current pulse was brief?)
What determines the space constant (l) ?
For long current pulses we can ignore membrane capacitance, so the circuit simplifies to;
More current will flow along the inside of the axon (i.e. the voltage change will travel
further) if;
Ri (resistance of the axoplasm ) is lower
Rm (‘leakage’ resistance across the membrane) is greater
An analogy: a leaky hosepipe
More water will flow out of the end of the pipe if its diameter is greater (fire hose vs garden
hose), and if the number of leaks is smaller
How does l vary with the diameter of an axon?
Membrane resistance Rm is proportional to the area of
membrane per unit length .
So, Rm is proportional to the circumference of the axon (2 p r)
Longitudinal axoplasmic resistance (Ri) per unit length is
proportional to cross sectional area (p r2)
As the diameter of an axon increases Rm decreases linearly,
whereas Ri decreases as the square root of the diameter.
Because l = Sqrt(Rm/Ri)
lincreases proportional to the square root of the axon diameter.
Thus, a signal will passively propagate a longer distance in a fat
axon than in a skinny axon.