Download Model of Skeletal Muscle Energy Metabolism

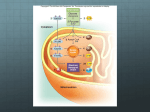
MATERIALS S2: METABOLIC REACTIONS FLUX EXPRESSIONS
The flux expressions for the compartmentalized lumped metabolic reactions that convert substrates to products in the two subcellular compartments (cytosol and mitochondria) in coupled
with the energy controller pairs ATP-ADP and NADH-NAD+ are written here from the generalized reaction flux expression (equation (5) of the manuscript) which is based on a phenomenological one-step Michaelis-Menten kinetics for enzymatic reactions. These expressions differ
from those of our previous model [1] through their dependencies on the compartmentalized (cytosolic or mitochondrial) metabolites concentrations, including the compartmentalized energy
controller ratios ATP/ADP and NADH/NAD+. As necessary, further descriptions are given below for the individual reactions and the reaction flux expressions.
Reactions in Cytosol
1. Glucose Utilization
GLCG6P
GLC  ATP  G6P  ADP

 V
GLCG6P

 1  Ccyt,G6P
G6P

KGLC
G6P

Ccyt,ATP


Ccyt,ADP

Ccyt,ATP
  K PS+

GLC

G6P


Ccyt,ADP


Ccyt,GLC

KGLCG6P

Ccyt,GLC
Ccyt,G6P

 G6P
1 K
KGLCG6P
GLCG6P







This reaction is catalyzed by the enzyme hexokinase which is inhibited by G6P ([5], Ch. 15; [6], Ch. 19).
The exact inhibition mechanism in-vivo is not well known. Therefore, a combination of noncompetitive
and product inhibition mechanism ([7], Ch. 3) is considered, which effectively modifies the Vmax as well as
the Km of the reaction.
2. Glycogen Synthesis
G6PGLY
G6P  ATP  GLY  ADP  2 PI
Ccyt,ATP

  Ccyt,G6P





Ccyt,ADP
  KG6PGLY 
 VG6PGLY 
Ccyt,ATP  
Ccyt,G6P 
 PS+
 KG6PGLY  C
1 K

cyt,ADP  
G6PGLY 

This is a sum of 4 enzymatic reactions G6P  G1P, G1P+UTP  UDP-GLC + 2 PI, UDP-GLC + GLYn
 UDP + GLYn+1 and UDP+ATP  UTP+ADP catalyzed by the enzymes phosphoglucomutase, UDPglucose pyrophosphorylase, glycogen synthase, and nucleoside diphosphokinase ([5], Ch. 20; [6], Ch. 23).
3. Glycogen Breakdown
GLYG6P
GLY  PI  G6P
Ccyt,AMP

  Ccyt,GLYCcyt,PI


Ccyt,ATP
KGLYG6P


 VGLYG6P
Ccyt,AMP  
Ccyt,GLYCcyt,PI
 PS
 KGLYG6P  C
1 K
cyt,ATP  
GLY G6P







This is a sum of 2 enzymatic reactions GLY + PI  G1P and G1P  G6P catalyzed by the enzymes glycogen phosphorylase and phosphoglucomutase ([5], Ch. 20; [6], Ch. 23). The activity of glycogen phosphorylase is regulated by AMP and ATP; AMP acts as a positive effector (activator) and ATP acts a negative effector (inhibitor) by competing with AMP. So the reaction is controlled by CAMP/CATP ratio.
G6P  ATP  2 GA3P  ADP
Ccyt,ATP


Ccyt,G6P





Ccyt,ADP
  KG6PGA3P 
 VG6PGA3P 
Ccyt,ATP  
Ccyt,G6P 
 PS+
 KG6PGA3P  C
1 K

cyt,ADP  
G6PGA3P 

4. Glucose 6-Phosphate Breakdown
G6PGA3P
This is a sum of 4 enzymatic reactions G6P  F6P, F6P + ATP  F16BP + ADP, F16BP  DHAP +
GA3P, and DHAP  GA3P catalyzed by the enzymes phosphoglucose isomerase, phosphofructokinase,
aldolase, and triose phosphate isomerase ([5], Ch. 15; [6], Ch. 19).
GA3P  PI  NAD   13BPG  NADH
5. Glyceraldehyde 3-Phosphate Breakdown
GA3P13BPG
Ccyt,NAD+


Ccyt,NADH
 VGA3P13BPG 
 RS
Ccyt,NAD+
 K GA3P13BPG 
Ccyt,NADH

  Ccyt,GA3PCcyt,PI

  K GA3P13BPG

Ccyt,GA3PCcyt,PI
  1 
K GA3P13BPG







This reaction is catalyzed by the enzyme glyceraldehyde 3-phosphate dehydrogenase and is known to be
reversible ([5], Ch. 15; [6], Ch. 19). Since |G| of the reaction is non-zero, we consider it as irreversible.
6. Pyruvate Production
13BPG PYR
13BPG  2 ADP  PYR  2 ATP
Ccyt,ADP

  Ccyt,13BPG




Ccyt,ATP
K13BPG PYR 



 V13BPG PYR
Ccyt,ADP  
Ccyt,13BPG 
 PS
 K13BPG PYR 
  1
Ccyt,ATP  
K13BPG PYR 

This is a sum of 4 enzymatic reactions 13BPG + ADP  3PG + ATP, 3PG  2PG, 2PG  PEP, and
PEP + ADP  PYR+ATP catalyzed by the enzymes phosphoglycerate kinase, phosphoglycerate mutase,
enolase, and pyruvate kinase ([5], Ch. 15; [6], Ch. 19).
7. Pyruvate Reduction
PYR LAC
PYR  NADH  LAC  NAD 
Ccyt,NADH

  Ccyt,PYR



Ccyt,NAD+
K PYR LAC 




 VPYR LAC
 RS+
Ccyt,NADH  
Ccyt,PYR 
 K PYR  LAC 
 1
Ccyt,NAD+  
K PYR  LAC 


This is an important reaction in skeletal muscle metabolism. When oxygen availability is limited (e.g.,
during muscle ischemia or intense muscle activities), NADH in cytosol can accumulate and reduce pyruvate to lactate with the help of the enzyme lactate dehydrogenase ([5], Ch. 15; [6], Ch. 19).
1
LAC  NAD  PYR  NADH
Ccyt,NAD+

  Ccyt,LAC




Ccyt,NADH
  K LAC PYR 
LACPYR  VLACPYR 
 RSCcyt,NAD+  
Ccyt,LAC 
 K LAC PYR 
  1 
K LAC PYR 
Ccyt,NADH  

This is the reverse lactate dehydrogenase reaction. During aerobic metabolism, NAD+ in cytosol can increase and oxidize lactate to pyruvate.
8. Lactate Oxidation
9. Alanine Production
PYR ALA
PYR  ALA
 Ccyt,PYR



K PYR ALA 

 VPYR ALA
Ccyt,PYR 

 1 K

PYR  ALA 

GA3P  3 FAC  NADH  TGL  3 CoA  PI  NAD
Ccyt,NADH

  Ccyt,GA3P Ccyt,FAC 



Ccyt,NAD+
K GA3P TGL



 VGA3P TGL
 RS+
Ccyt,NADH   Ccyt,GA3P Ccyt,FAC 
 K GA3P TGL 
 1

Ccyt,NAD+  
K GA3P TGL 


10. Triglyceride Synthesis
GA3P TGL
This is a sum of several enzymatic reactions. It can be viewed as lumping of reactions GA3P  DHAP,
DHAP + NADH  G3P + NAD+, and G3P + 3 FAC  TGL + 3 CoA + PI. The major enzymes are glycerol-3 phosphate dehydrogenase and acyltransferase ([5], Ch. 21; [6], Ch. 24). The synthesis of triglycerides from glycerol is neglected here as the activity of the enzyme glycerol kinase is negligible in muscle.
11. Lipolysis (Triglycerides Hydrolysis)
TGLFFA
12. Fatty Acyl-CoA Formation
FFA FAC
TGL  GLR  3 FFA
 Ccyt,TGL 


K TGLFFA 

 VTGL FFA
Ccyt,TGL 

 1 K

TGL  FFA 

FFA  CoA  2 ATP  FAC  2 ADP  2 PI
Ccyt,ATP


Ccyt,ADP
 VFFA FAC 
Ccyt,ATP
 PS+
 K FFA FAC 
Ccyt,ADP

  Ccyt,FFA Ccyt,CoA

K FFA FAC

  Ccyt,FFA Ccyt,CoA
  1
K FFA FAC







This reaction is also called fatty acid activation in which the enzyme is fatty acid thiokinase. The activated
fatty acid is transported into the mitochondrial matrix through the carnitine shuttle which is subsequently
oxidized to ACoA by several enzymatic reactions ([5], Ch.21; [6], Ch.24).
ATP  ADP  PI
13. ATP Hydrolysis
2
ATPADP

 V
  ATPADP
 1  Ccyt,PI
PI

K ATP
 ADP

Ccyt,ATP


Ccyt,ADP

Ccyt,ATP
  K PS+

ATP

ADP


Ccyt,ADP







This reaction is catalyzed by the enzyme ATPase and is the primary source of energy supply for muscle
contraction ([5], Ch.14; [6], Ch.17). This reaction is inhibited by ADP and PI.
PCR  ADP  CR  ATP
Ccyt,ADP

  Ccyt,PCR 


Ccyt,ATP
K PCR CR 




 VPCR CR
Ccyt,ADP  
Ccyt,PCR 
 PS K PCR CR  C
1 K

cyt,ATP  
PCR CR 

14. Phosphocreatine Breakdown
PCR CR
This is an ATP buffer reaction catalyzed by the enzyme creatine kinase. It functions to maintain ATP homeostasis during muscle contraction ([5], Ch.14; [6], Ch.17). It is the primary source of immediate energy
supply during the transitions from rest to exercise.
CR  ATP  PCR  ADP
15. Phosphocreatine Synthesis
CR PCR
Ccyt,ATP


Ccyt,ADP
 VCR PCR 
Ccyt,ATP
 PS+
 KCR PCR  C
cyt,ADP

  Ccyt,CR

  KCR PCR
Ccyt,CR

1 K
CR  PCR







This is the reverse creatine kinase reaction where creatine is phosphorylated to phosphocreatine.
AMP  ATP  ADP  ADP
16. Adenylate Kinase – Forward
AMPADP
Ccyt,ATP


Ccyt,ADP
 VAMPADP 
Ccyt,ATP
 PS+
K

AMP

ADP

Ccyt,ADP

  Ccyt,AMP

  K AMPADP
Ccyt,AMP

1


K AMPADP







ADP  ADP  AMP  ATP
Ccyt,ADP

  Ccyt,ADP





Ccyt,ATP
  K ADPAMP 
 VADPAMP 
Ccyt,ADP  
Ccyt,ADP 
 PSK

1

ADP

AMP

Ccyt,ATP  
K ADPAMP 

17. Adenylate Kinase – Reverse
ADPAMP
Reactions in Mitochondria
18. Pyruvate Oxidation
PYR  CoA  NAD   ACoA  NADH  CO 2
3
PYR ACoA
Cmit,NAD+


Cmit,NADH
 VPYR ACoA 
Cmit,NAD+
 RS
 K PYR ACoA 
Cmit,NADH

  Cmit,PYR Cmit,CoA

K PYR ACoA

Cmit,PYR Cmit,CoA

1 K
PYR  ACoA







This is the first reaction inside the mitochondrial matrix in which ACoA is formed from the oxidative decarboxylation of pyruvate (carbohydrate oxidation) by the enzyme pyruvate dehydrogenase leading to the
TCA cycle ([5], Ch.16; [6], Ch.20).
FAC  7 CoA  14 NAD  8 ACoA  14 NADH
Cmit,NAD+

  Cmit,FACCmit,CoA 



Cmit,NADH
K FACACoA



 VFACACoA
Cmit,NAD+  
Cmit,FACCmit,CoA 
 RS
 K FACACoA 
1 K

C
FAC ACoA

mit,NADH


19. Fatty Acyl-CoA Oxidation
FACACoA
This reaction producing ACoA from the activated fatty acid (fat) inside the mitochondrial matrix is highly
complex. It is the result of combining 7 cycles of reactions in which each cycle consists of 4 enzymatic
reactions catalyzed by the enzymes acyl-CoA dehydrogenase, enoyl-CoA hydratase, beta-hydroxyacylCoA dehydrogenase, and acyl-CoA acetyletransferase (thiolase) ([5], Ch. 21; [6], Ch. 24). For simplicity,
the reducing equivalents FAD and FADH2 are considered equivalent to NAD+ and NADH, as they consume equal amount of O2.
ACoA  OXA  CIT  CoA
20. Citrate Production
ACoACIT
 Cmit,ACoACmit,OXA

K ACoACIT
 VACoACIT 
 1  Cmit,ACoACmit,OXA

K ACoACIT







This is the first reaction of TCA cycle catalyzed by the enzyme citrate synthase ([5], Ch. 16; [6], Ch. 20).
CIT  NAD   AKG  NADH  CO 2
21. Alpha-Ketoglutarate Production
CITAKG
Cmit,NAD+


Cmit,NADH
 VCIT AKG 
Cmit,NAD+
 RS
 K CIT AKG 
Cmit,NADH

  Cmit,CIT

  K CITAKG
Cmit,CIT

1 K
CIT  AKG







This is a sum of two enzymatic reactions CIT ↔ ICIT and ICIT+NAD+ → AKG+CO2+NADH catalyzed
by the enzymes aconitase and isocitrate dehydrogenase.
22. Succinyl-CoA Production
AKG SCoA
AKG  CoA  NAD  SCoA  NADH  CO2
Cmit,NAD+


Cmit,NADH
 VAKG SCoA 
 RS
C
+
 K AKG SCoA  mit,NAD
Cmit,NADH

4
  Cmit,AKG Cmit,CoA

K AKG SCoA

  Cmit,AKG Cmit,CoA
  1 
K AKG SCoA







23. Succinate Production
SCoA SUC
SCoA  GDP  PI  SUC  CoA  GTP
Cmit,ADP

  Cmit,SCoA Cmit,PI 



Cmit,ATP
KSCoA SUC


 VSCoA SUC 
Cmit,ADP   Cmit,SCoA Cmit,PI 
 PS
 KSCoA SUC  C
 1 K

mit,ATP  
SCoA SUC


Because the reaction GTP+ADP  GDP+ATP is in fast equilibrium, we assume the GTP/GDP ratio proportional to the ATP/ADP ratio ([5], Ch. 16; [6], Ch. 20).
24. Malate Production
SUCMAL
SUC  NAD  MAL  NADH
Cmit,NAD+

  Cmit,SUC




Cmit,NADH
  KSUCMAL 
 VSUCMAL 
 RS

C
Cmit,SUC 
+
 K MALOXA  mit,NAD   1 
KSUCMAL 
Cmit,NADH  

This is a sum of two enzymatic reactions SUC + FAD → FUM + FADH2 & FUM ↔ MAL catalyzed by
the enzymes succinate dehydrogenase and fumarate ([5], Ch.16; [6], Ch.20); FAD and FADH2 are considered equivalent to NAD+ and NADH, as they consume equal amount of O2.
MAL  NAD   OXA  NADH
25. Oxaloacetate Production
MALOXA
26. Oxygen Utilization
O2H2O
Cmit,NAD+


Cmit,NADH
 VMALOXA 
 RS
C
+
 K MALOXA  mit,NAD
Cmit,NADH

  Cmit,MAL

  K MALOXA

Cmit,MAL
  1 
K MALOXA







O2  6 ADP  6 PI  2 NADH  2 H 2O  6 ATP  2 NAD 
Cmit,ADP


Cmit,ATP
 VO2H2O 
Cmit,ADP
 PS
 K O2H2O  C
mit,ATP

Cmit,NADH



Cmit,NAD+

Cmit,NADH
  RS
  K O2H2O  C

mit,NAD +
F
  Cmit,O2
Cmit,PI

K O2H2O

F
  Cmit,O2
Cmit,PI
  1 
K O2H2O







This is also the ATP synthesis reaction. This is a sum of several enzymatic reactions at complex I–V that
constitute the electron transport chain and oxidative phosphorylation inside the mitochondrial matrix ([5],
Ch.19; [6], Ch.21); FAD and FADH2 are considered equivalent to NAD+ and NADH as they consume
equal amount of O2. Furthermore, 1 NADH is assumed to produce 3 ATP (i.e., P/O ratio = 3; a perfect
coupling with negligible proton leak).
5
Reference List
1. Dash RK, Li Y, Kim J, Saidel GM, Cabrera ME (2008) Modeling cellular metabolism and energetics in skeletal muscle: large-scale parameter estimation and sensitivity analysis. IEEE Trans
Biomed Eng 55: 1298-1318.
2. Dash RK, Bassingthwaighte JB (2004) Blood HbO2 and HbCO2 dissociation curves at varied O2,
CO2, pH, 2,3-DPG and temperature levels. Ann Biomed Eng 32: 1676-1693.
3. Dash RK, Bassingthwaighte JB (2006) Simultaneous blood-tissue exchange of oxygen, carbon dioxide, bicarbonate, and hydrogen ion. Ann Biomed Eng 34: 1129-1148.
4. Geers C, Gros G (2000) Carbon dioxide transport and carbonic anhydrase in blood and muscle.
Physiol Rev 80: 681-715.
5. Nelson D, Cox M (2000) Lehninger Principles of Biochemistry (third edition). Worth Publishers,
New York.
6. Stryer L (1996) Biochemistry (fourth edition). W.H. Freeman and Company, New York.
7. Segel I (1993) Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems. Wiley-Interscience, New York.
6