* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Neural Networks - National Taiwan University
Microneurography wikipedia , lookup
Eyeblink conditioning wikipedia , lookup
Neuroeconomics wikipedia , lookup
Binding problem wikipedia , lookup
Multielectrode array wikipedia , lookup
Neuroethology wikipedia , lookup
Holonomic brain theory wikipedia , lookup
Neural oscillation wikipedia , lookup
Optogenetics wikipedia , lookup
Sparse distributed memory wikipedia , lookup
Neural coding wikipedia , lookup
Neuropsychopharmacology wikipedia , lookup
History of artificial intelligence wikipedia , lookup
Neural modeling fields wikipedia , lookup
Artificial intelligence wikipedia , lookup
Biological neuron model wikipedia , lookup
Synaptic gating wikipedia , lookup
Central pattern generator wikipedia , lookup
Pattern recognition wikipedia , lookup
Hierarchical temporal memory wikipedia , lookup
Development of the nervous system wikipedia , lookup
Metastability in the brain wikipedia , lookup
Neural engineering wikipedia , lookup
Nervous system network models wikipedia , lookup
Artificial neural network wikipedia , lookup
Catastrophic interference wikipedia , lookup
Convolutional neural network wikipedia , lookup
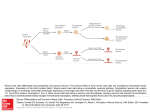
Yung-Pin, Tsai Information Management National Taiwan University Introduction to Neural Networks Human and Artificial Neurons An Engineering Approach Architecture of neural networks The Learning Process A Neural Approach to Topological Optimization of Communication Networks, With Reliability Constraints A New Method for Response Integration in Modular Neural Networks using Type-2 Fuzzy Logic for Biometric Systems • What is neural network? • Why use neural network? • Neural networks versus conventional computers An Artificial Neural Network (ANN) is an information processing paradigm that is inspired by the way biological nervous systems. composed of a large number of highly interconnected processing elements (neurons) . ANNs, like people, learn by example ◦ (Learning, Recall, Generalization) An ANN is configured for a specific application, such as pattern recognition or data classification, through a learning process. Involves adjustments to the synaptic connections that exist between the neurons. With their remarkable ability to derive meaning from complicated or imprecise data. A trained neural network can be thought of as an "expert" in the category of information it has been given to analyze. To provide projections given new situations of interest and answer "what if" questions Other advantages : ◦ ◦ ◦ ◦ Adaptive learning Self-Organization Real Time Operation Fault Tolerance via Redundant Information Coding Conventional computers use an algorithmic approach to problem solving. ◦ i.e. the computer follows a set of instructions in order to solve a problem. That restricts the problem solving capability of conventional computers to problems that we already understand and know how to solve. But computers would be so much more useful if they could do things that we don't exactly know how to do. Introduction to Neural Networks Human and Artificial Neurons An Engineering Approach Architecture of neural networks The Learning Process A Neural Approach to Topological Optimization of Communication Networks, With Reliability Constraints A New Method for Response Integration in Modular Neural Networks using Type-2 Fuzzy Logic for Biometric Systems How the Human Brain Learn? From Human Neurons to Artificial Neurons A typical neuron collects signals from others through a host of fine structures called dendrites. The neuron sends out spikes of electrical activity through a long, thin stand known as an axon Learning occurs by changing the effectiveness of the synapses so that the influence of one neuron on another changes. We conduct these neural networks by first trying to deduce the essential features of neurons and their interconnections. However because our knowledge of neurons is incomplete and our computing power is limited, our models are necessarily gross idealizations of real networks of neurons. Introduction to Neural Networks Human and Artificial Neurons An Engineering Approach Architecture of neural networks The Learning Process A Neural Approach to Topological Optimization of Communication Networks, With Reliability Constraints A New Method for Response Integration in Modular Neural Networks using Type-2 Fuzzy Logic for Biometric Systems A Simple Neuron Firing Rules Pattern Recognition A More Complicated Neuron An artificial neuron is a device with many inputs and one output. The neuron has two modes of operation; the training mode and the using mode. ◦ In the training mode, the neuron can be trained to fire (or not), for particular input patterns. ◦ In the using mode, when a taught input pattern is detected at the input, its associated output becomes the current output. If the input pattern does not belong in the taught list of input patterns, the firing rule is used to determine whether to fire or not. A firing rule determines how one calculates whether a neuron should fire for any input pattern. A simple firing rule can be implemented by using Hamming distance technique: ◦ Take a collection of training patterns for a node, some of which cause it to fire (the 1-taught set of patterns) and others which prevent it from doing so (the 0-taught set). ◦ Patterns not in the collection cause the node to fire if, on comparison , they have more input elements in common with the 'nearest' pattern in the 1-taught set than with the 'nearest' pattern in the 0-taught set. ◦ If there is a tie, then the pattern remains in the undefined state. Ex: a 3-input neuron is taught to output 1 when the input (X1,X2 and X3) is 111 or 101 and to output 0 when the input is 000 or 001. X1: 0 0 0 0 1 1 1 1 X2: 0 0 1 1 0 0 1 1 X3: 0 1 0 1 0 1 0 1 OUT: 0 0 0/1 0/1 0/1 1 0/1 1 X1: 0 0 0 0 1 1 1 1 X2: 0 0 1 1 0 0 1 1 X3: 0 1 0 1 0 1 0 1 OUT: 0 0 0 0/1 0/1 1 1 1 Hamming distance technique the firing rule gives the neuron a sense of similarity and enables it to respond 'sensibly' to patterns not seen during training. Pattern recognition can be implemented by using a feed-forward neural network that has been trained accordingly. During training, the network is trained to associate outputs with input patterns. When the network is used, it identifies the input pattern and tries to output the associated output pattern. The power of neural networks comes to life when a pattern that has no output associated with the input. Top neuron Middle neuron Bottom neuron X11: 0 0 0 0 1 1 1 1 X12: 0 0 1 1 0 0 1 1 X13: 0 1 0 1 0 1 0 1 OUT: 0 0 1 1 0 0 1 1 X21: 0 0 0 0 1 1 1 1 X22: 0 0 1 1 0 0 1 1 X23: 0 1 0 1 0 1 0 1 OUT: 1 0/1 1 0 0/1 0 X31: 0 0 0 0 1 1 1 1 X32: 0 0 1 1 0 0 1 1 X33: 0 1 0 1 0 1 0 1 OUT: 1 0 1 1 0 0 1 0 0/1 0/1 examples In this case, it is obvious that the output should be all blacks since the input pattern is almost the same as the 'T' pattern. Here also, it is obvious that the output should be all whites since the input pattern is almost the same as the 'H' pattern. Here, the top row is 2 errors away from the a T and 3 from an H. So the top output is black. The middle row is 1 error away from both T and H so the output is random. The bottom row is 1 error away from T and 2 away from H. Therefore the output is black. The total output of the network is still in favor of the T shape. The previous neuron doesn't do anything that conventional computers don't do already. A more sophisticated neuron is the McCulloch and Pitts model (MCP). These weighted inputs are then added together and if they exceed a pre-set threshold value, the neuron fires. In any other case the neuron does not fire. In mathematical terms, the neuron fires if and only if: ◦ X1W1 + X2W2 + X3W3 + ... > T The addition of input weights and of the threshold makes this neuron a very flexible and powerful one. The MCP neuron has the ability to adapt to a particular situation by changing its weights and/or threshold. Various algorithms exist that cause the neuron to 'adapt'; the most used ones are the Delta rule and the back error propagation. The former is used in feed-forward networks and the latter in feedback networks. The output is ◦ 1 if W0 *I0 + W1 * I1 + Wb > 0 ◦ 0 if W0 *I0 + W1 * I1 + Wb <= 0 We want it to learn simple OR: output a 1 if either I0 or I1 is 1. The network adapts as follows: ◦ Δ Wi = η * (D-Y)* Ii ◦ where η is the learning rate, D is the desired output, and Y is the actual output. • This is called the Perceptron Learning Rule, and goes back to the early 1960's. Wb Input 0 Input 1 W0 W1 + fH(x) Output Since (D-Y)=0 for all patterns, the weights cease adapting. Network converges on a hyper-plane decision surface ◦ I1 = (W0/W1)I0 + (Wb/W1) Developments from the simple perceptron: ◦ Back-Propagated Delta Rule Networks (BPN) ◦ Radial Basis Function Networks (RBF) Introduction to Neural Networks Human and Artificial Neurons An Engineering Approach Architecture of neural networks The Learning Process A Neural Approach to Topological Optimization of Communication Networks, With Reliability Constraints A New Method for Response Integration in Modular Neural Networks using Type-2 Fuzzy Logic for Biometric Systems Feed-forward networks Feedback networks Network layers Perceptrons Feed-forward ANNs (figure 1) allow signals to travel one way only; from input to output. There is no feedback They are extensively used in pattern recognition. Feedback networks can have signals travelling in both directions by introducing loops in the network. Feedback networks are very powerful and can get extremely complicated. Feedback networks are dynamic; their 'state' is changing continuously until they reach an equilibrium point. They remain at the equilibrium point until the input changes and a new equilibrium needs to be found. Input layer: ◦ The activity of the input units represents the raw information that is fed into the network. Hidden layer: ◦ The activity of each hidden unit is determined by the activities of the input units and the weights on the connections between the input and the hidden units. Output layer: ◦ The behaviour of the output units depends on the activity of the hidden units and the weights between the hidden and output units. The most influential work on neural nets in the 60's went under the heading of 'perceptrons' a term coined by Frank Rosenblatt. Perceptrons mimic the basic idea behind the mammalian visual system They were mainly used in pattern recognition even though their capabilities extended a lot more. Introduction to Neural Networks Human and Artificial Neurons An Engineering Approach Architecture of neural networks The Learning Process A Neural Approach to Topological Optimization of Communication Networks, With Reliability Constraints A New Method for Response Integration in Modular Neural Networks using Type-2 Fuzzy Logic for Biometric Systems Pattern Mapping Methods Two Major Categories of Neural Networks Transfer function The Back-Propagation Algorithm associative mapping ◦ auto-association: Associated with itself and the states of input and output units coincide. This is used to provide pattern completion. ◦ hetero-association: nearest-neighbor recall: find the stored input that closely matches the stimulus and respond output with distance measure ex: Hamming or Euclidean distance interpolative recall: takes the stimulus and interpolates the entire set of stored inputs to produce the corresponding output. regularity detection ◦ in which units learn to respond to particular properties of the input patterns. ◦ Whereas in associative mapping the network stores the relationships among patterns, in regularity detection the response of each unit has a particular 'meaning'. This type of learning mechanism is essential for feature discovery and knowledge representation. fixed networks in which the weights cannot be changed, ie dW/dt=0. In such networks, the weights are fixed a priori according to the problem to solve. adaptive networks which are able to change their weights, ie dW/dt != 0. Supervised learning: (off-line) which incorporates an external teacher, so that each output unit is told what its desired response to input signals ought to be. ◦ error-correction learning ◦ reinforcement learning ◦ stochastic learning. Unsupervised learning: (on-line) uses no external teacher and is based upon only local information. Self-organization. ◦ Hebbian learning ◦ Competitive learning. For linear units, the output activity is proportional to the total weighted input. For threshold units, the output is set at one of two levels, depending on whether the total input is greater than or less than some threshold value. For sigmoid units, the output varies continuously but not linearly as the input changes. Sigmoid units bear a greater resemblance to real neurones than do linear or threshold units, but all three must be considered rough approximations. The hidden layer learns to recode (or to provide a representation for) the inputs. More than one hidden layer can be used F(x) = 1 / (1 + e -k ∑ (wixi) ) ◦ Shown for k = 0.5, 1 and 10 Using a nonlinear function which approximates a linear threshold allows a network to approximate nonlinear functions It is a supervised learning method, and is an implementation of the Delta rule. The delta rule is a gradient descent learning rule for updating the weights of the artificial neurons in a single-layer perceptron. Error Function: For a neuron with activation function the delta rule for j‘s ith weight is given by: (gradient for weight) a gradient descent algorithm for learning the weights into hidden units as well as output units The learning rule: Δwji = ηδjxi For output units: δj = (tj - xj) g’(hj) For hidden units δj = [∑k δk wkj] g’(hj) Introduction to Neural Networks Human and Artificial Neurons An Engineering Approach Architecture of neural networks The Learning Process A Neural Approach to Topological Optimization of Communication Networks, With Reliability Constraints A New Method for Response Integration in Modular Neural Networks using Type-2 Fuzzy Logic for Biometric Systems Hosam M. F. AboElFotoh and Loulwa S. Al-Sumait IEEE TRANSACTIONS ON RELIABILITY, VOL. 50, NO. 4, DECEMBER 2001 Optimization ANNs are concerned with the minimization of a particular cost function with respect to certain constraints. ANN are shown to be capable of highly efficient optimization. (http://en.wikibooks.org/wiki/Artificial_Neural_Netw orks/Optimization) The first ANN for combinatorial OPTI-net was introduced in (1985), and referred to as Hopfield neural network. Since then, OPTInets have been successful in constraintoptimization problems. The objective is to find the topological layout of links, at minimal cost, under the constraint: allterminal network reliability is not less than a given level of system reliability. The problem is mapped onto an optimization ANN (OPTI-net) by constructing an energy function whose minimization process drives the neural network into one of its stable states. OPTI-net favors states: ◦ Overall reliability greater than or equal to a threshold value. ◦ has the lowest total cost. Hysteresis McCulloch–Pitts neuron model is used in the solution, due to its performance and fast convergence. Considering NP-hard complexity of the exact reliability calculation & iterative behavior of the neural networks, bounds for the all-terminal reliability: ◦ introduces new upper and lower bounds that are functions of the link selection and uses them to represent the network reliability. The strengths of this neural network approach are very slowly increasing computation time with respect to network size, effective optimization, and flexibility. solutions even in search spaces up to ≈1016 for a fully connected network with 50 vertexes. The OPTI-net is the first approach to be applied on such large networks. The simulation results show that the neural approach is more efficient in designing networks of large sizes compared to other heuristic techniques. ◦ Compared with B&B(Branch and Bound), GA(Genetic Algorithm) Introduction to Neural Networks Human and Artificial Neurons An Engineering Approach Architecture of neural networks The Learning Process Application of neural networks A Neural Approach to Topological Optimization of Communication Networks, With Reliability Constraints A New Method for Response Integration in Modular Neural Networks using Type-2 Fuzzy Logic for Biometric Systems Jerica Urias, Denisse Hidalgo, Patricia Melin, and Oscar Castillo Proceedings of International Joint Conference on Neural Networks, Orlando, Florida, USA, August 12-17, 2007 a new method for response integration in modular neural networks using type-2 fuzzy logic. The modular neural networks were applied to human person recognition. Biometric authentication is used to achieve person recognition. ◦ face, fingerprint, and voice. The response integration method of the modular neural network has the goal of combining the responses of the modules to improve the recognition rate of the individual modules. One module for voice, one module for face recognition, and one module for fingerprint recognition. At the top, we have the decision unit integrating the results from the three modules. ◦ decision unit is implemented with a type-2 fuzzy system. • Two principle components: local experts and an integration unit • Combined estimators Combined estimators may be able to exceed the limitation of a single estimator. The idea also shares conceptual links with the "divide and conquer" methodology. When using a modular network, a given task is split up among several local experts NNs. http://www.doc.ic.ac.uk/~nd/surprise_96/j ournal/vol4/cs11/report.html http://www.cs.stir.ac.uk/~lss/NNIntro/InvSl ides.html http://www.cs.indiana.edu/classes/b351gass/Notes/backprop.html http://www.statsoft.com/textbook/stneune t.html#multilayerb