* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download lecture05_09
Transcription factor wikipedia , lookup
Designer baby wikipedia , lookup
Gene expression profiling wikipedia , lookup
No-SCAR (Scarless Cas9 Assisted Recombineering) Genome Editing wikipedia , lookup
Epigenetics of human development wikipedia , lookup
Microevolution wikipedia , lookup
Transposable element wikipedia , lookup
Genome evolution wikipedia , lookup
Primary transcript wikipedia , lookup
Cre-Lox recombination wikipedia , lookup
Pathogenomics wikipedia , lookup
Nucleic acid tertiary structure wikipedia , lookup
Non-coding DNA wikipedia , lookup
Human genome wikipedia , lookup
Site-specific recombinase technology wikipedia , lookup
Point mutation wikipedia , lookup
Microsatellite wikipedia , lookup
Metagenomics wikipedia , lookup
Genome editing wikipedia , lookup
Computational phylogenetics wikipedia , lookup
Helitron (biology) wikipedia , lookup
Artificial gene synthesis wikipedia , lookup
Therapeutic gene modulation wikipedia , lookup
Smith–Waterman algorithm wikipedia , lookup
From Pairwise to
Multiple Alignment
WHATS TODAY?
• Multiple Sequence Alignment- CLUSTAL
• MOTIF search
Multiple Sequence Alignment
MSA
VTISCTGSSSNIGAG-NHVKWYQQLPG
VTISCTGTSSNIGS--ITVNWYQQLPG
LRLSCSSSGFIFSS--YAMYWVRQAPG
LSLTCTVSGTSFDD--YYSTWVRQPPG
PEVTCVVVDVSHEDPQVKFNWYVDG-ATLVCLISDFYPGA--VTVAWKADS-AALGCLVKDYFPEP--VTVSWNSG--VSLTCLVKGFYPSD--IAVEWWSNG--
Like pairwise alignment BUT compare n
sequences instead of 2
Rows represent individual sequences
Columns represent ‘same’ position
Gaps allowed in all sequences
How to find the best MSA
GTCGTAGTCGGCTCGAC
GTCTAGCGAGCGTGAT
GCGAAGAGGCGAGC
GCCGTCGCGTCGTAAC
GTCGTAGTCG-GC-TCGAC
GTC-TAG-CGAGCGT-GAT
GC-GAAG-AG-GCG-AG-C
GCCGTCG-CG-TCGTA-AC
Score : 4/4 =1 , 3/4 =0.75 , 2/4=0.5 , 1/4= 0
1*1
2*0.75
11*0.5
Score=8
4*1
11*0.75
2*0.5
Score=13.25
Alignment of 3 sequences:
Complexity: length A length B length C
Aligning 100 proteins, 1000 amino acids each
Complexity: 10300 table cells
Calculation time: beyond the big bang!
Feasible Approach
Progressive alignment (Feng & Doolittle).
• Based on pairwise alignment scores
– Build n by n table of pairwise scores
• Align similar sequences first
– After alignment, consider as single sequence
– Continue aligning with further sequences
– For n sequences, there are n(n-1)/2 pairs
GTCGTAGTCG-GC-TCGAC
GTC-TAG-CGAGCGT-GAT
GC-GAAG-AG-GCG-AG-C
GCCGTCG-CG-TCGTA-AC
1
2
3
4
GTCGTAGTCG-GC-TCGAC
GTC-TAG-CGAGCGT-GAT
GC-GAAGAGGCG-AGC
GCCGTCGCGTCGTAAC
1
2
3
4
GTCGTA-GTCG-GC-TCGAC
GTC-TA-G-CGAGCGT-GAT
G-C-GAAGA-G-GCG-AG-C
G-CCGTCGC-G-TCGTAA-C
CLUSTAL method
Applies Progressive Sequence Alignment
• Higgins and Sharp 1988
– ref: CLUSTAL: a package for performing
multiple sequence alignment on a
microcomputer. Gene, 73, 237–244. [Medline]
An approximation strategy (heuristic
algorithm) yields a possible alignment, but
not necessarily the best one
Treating Gaps in CLUSTAL
• Penalty for opening gaps and additional
penalty for extending the gap
• Gaps found in initial alignment remain
fixed
• New gaps are introduced as more sequences
are added (decreased penalty if gap exists)
Other MSA Approaches
• Progressive approach
CLUSTALW (CLUSTALX)
PILEUP
T-COFFEE
• Iterative approach:
Repeatedly realign subsets of sequences.
MultAlin, DiAlign.
• Statistical Methods:
Hidden Markov Models (only for proteins)
SAM2K, MUSCLE
• Genetic algorithm
SAGA
Links to commonly used MSA tools
CLUSTALW
http://www.ebi.ac.uk/Tools/clustalw2/
T-COFFEE
http://www.ebi.ac.uk/t-coffee/
MUSCLE
http://www.ebi.ac.uk/muscle/
MAFFT
http://www.ebi.ac.uk/mafft/
Kalign
http://www.ebi.ac.uk/kalign/
CAUTION !!!
Different tools may give different results
Example : 7 different alignment tools produced 6 different
Estimated evolution trees
Wong et al., Science 319, January 2008
Motifs
• Motifs represent a short common sequence
– Regulatory motifs (TF binding sites)
– Functional site in proteins (DNA binding motif)
DNA Regulatory Motifs
• Transcription Factors bind to regulatory
motifs
– TF binding motifs are usually 6 – 20
nucleotides long
– Usually located near target gene, mostly
upstream the transcription start site
Transcription
Start Site
MCM1
SBF
MCM1
motif
SBF
motif
Gene X
Why are motifs interesting?
• A motif is evidence of binding
• A motif can help in developing hypotheses
regarding which protein is regulating the
expression of a specific genes
• Mutations at particular regulatory sites can
lead to disease
Challenges
• How to recognize a regulatory motif?
• Can we identify new occurrences of known
motifs in genome sequences?
• Can we discover new motifs within
upstream sequences of genes?
E. Coli promoter sequences
1. Motif Representation
• Exact motif: CGGATATA
• Consensus: represent only
deterministic nucleotides.
– Example: HAP1 binding sites in
5 sequences.
• consensus motif: CGGNNNTANCGG
• N stands for any nucleotide.
• Representing only consensus
loses information. How can this
be avoided?
CGGATATACCGG
CGGTGATAGCGG
CGGTACTAACGG
CGGCGGTAACGG
CGGCCCTAACGG
-----------CGGNNNTANCGG
Representing the motif as a profile
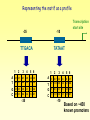
Transcription
start site
-35
-10
TTGACA
3
4
5 6
0.1 0.1
0.7 0.7
0.1
0.2
0.5
0.2
0.2 0.5
0.2 0.2
0.1 0.1
0.5
0.1
0.1 0.2
0.1 0.1
0.2
0.2 0.5
1
A
T
G
C
2
TATAAT
-35
0.1
A
T
G
C
1
2
3
4
0.1
0.7 0.2
0.6
0.5
0.1
0.7
0.1 0.5
0.2
0.2
0.8
0.1
0.1 0.1
0.1
0.1 0.0
0.1
0.1 0.2
0.1
0.1 0.1
-10
5 6
Based on ~450
known promoters
PSPM – Position Specific
Probability Matrix
• Represents a motif of length k (5)
• Count the number of occurrence of each nucleotide in
each position
1
2
3
4
5
A
10
25
5
70
60
C
30
25
80
10
15
T
50
25
5
10
5
G
10
25
10
10
20
PSPM – Position Specific
Probability Matrix
• Defines Pi{A,C,G,T} for i={1,..,k}.
– Pi (A) – frequency of nucleotide A in position i.
1
2
3
4
5
A
0.1
0.25
0.05
0.7
0.6
C
0.3
0.25
0.8
0.1
0.15
T
0.5
0.25
0.05
0.1
0.05
G
0.1
0.25
0.1
0.1
0.2
Identification of Known Motifs
within Genomic Sequences
• Motivation:
– identification of new genes controlled by the same
TF.
– Infer the function of these genes.
– Enable better understanding of the regulation
mechanism.
PSPM – Position Specific
Probability Matrix
• Each k-mer is assigned a probability.
– Example: P(TCCAG)=0.5*0.25*0.8*0.7*0.2
1
2
3
4
5
A
0.1
0.25
0.05
0.7
0.6
C
0.3
0.25
0.8
0.1
0.15
T
0.5
0.25
0.05
0.1
0.05
G
0.1
0.25
0.1
0.1
0.2
Detecting a Known Motif within a
Sequence using PSPM
• The PSPM is moved along the query sequence.
• At each position the sub-sequence is scored for a
match to the PSPM.
1
2
3
• Example:
A
0.1
0.25
0.05
sequence = ATGCAAGTCT…
4
5
0.7
0.6
C
0.3
0.25
0.8
0.1
0.15
T
0.5
0.25
0.05
0.1
0.05
G
0.1
0.25
0.1
0.1
0.2
Detecting a Known Motif within a
Sequence using PSPM
• The PSPM is moved along the query sequence.
• At each position the sub-sequence is scored for a
match to the PSPM.
1
2
3
• Example:
A
0.1
0.25
0.05
sequence = ATGCAAGTCT…
C
0.3
0.25
0.8
• Position 1: ATGCA
0.1*0.25*0.1*0.1*0.6=1.5*10-4
4
5
0.7
0.6
0.1
0.15
T
0.5
0.25
0.05
0.1
0.05
G
0.1
0.25
0.1
0.1
0.2
Detecting a Known Motif within a
Sequence using PSPM
• The PSPM is moved along the query sequence.
• At each position the sub-sequence is scored for a
match to the PSPM.
1
2
3
• Example:
A
0.1
0.25
0.05
sequence = ATGCAAGTCT…
C
0.3
0.25
0.8
• Position 1: ATGCA
0.1*0.25*0.1*0.1*0.6=1.5*10-4
• Position 2: TGCAA
0.5*0.25*0.8*0.7*0.6=0.042
4
5
0.7
0.6
0.1
0.15
T
0.5
0.25
0.05
0.1
0.05
G
0.1
0.25
0.1
0.1
0.2
Detecting a Known Motif within a
Sequence using PSSM
Is it a random match, or is it indeed an
occurrence of the motif?
PSPM -> PSSM (Probability Specific Scoring Matrix)
– odds score : Oi(n) where n {A,C,G,T} for i={1,..,k}
– defined as Pi(n)/P(n), where P(n) is background frequency.
Oi(n) increases => higher odds that n at position i is part of
a real motif.
PSSM as Odds Score Matrix
•
Assumption: the background frequency of each
nucleotide is 0.25.
1
2
3
4
1. Original PSPM (Pi): A 0.1
0.25
0.05 0.7
2. Odds Matrix (Oi):
A
5
0.6
1
2
3
4
5
0.4
1
0.2
2.8
2.4
3. Going to log scale we get an additive score,
Log odds Matrix (log2Oi):
A
1
2
3
4
5
-1.322
0
-2.322
1.485
1.263
Calculating using Log Odds Matrix
• Odds 0 implies random match;
Odds > 0 implies real match (?).
• Example: sequence = ATGCAAGTCT…
1
2
• Position 1: ATGCA
-1.32+0-1.32-1.32+1.26=-2.7
odds= 2-2.7=0.15
• Position 2: TGCAA
1+0+1.68+1.48+1.26 =5.42
odds=25.42=42.8
3
4
5
A
-1.32
0
-2.32
1.48
1.26
C
0.26
0
1.68
-1.32
-0.74
T
1
0
-2.32
-1.32
-2.32
G
-1.32
0
-1.32
-1.32
-0.32
Calculating the probability of a Match
ATGCAAG
• Position 1 ATGCA = 0.15
Calculating the probability of a Match
ATGCAAG
• Position 1 ATGCA = 0.15
• Position 2 TGCAA = 42.3
Calculating the probability of a Match
ATGCAAG
• Position 1 ATGCA = 0.15
• Position 2 TGCAA = 42.3
• Position 3 GCAAG = 0.18
Calculating the probability of a match
ATGCAAG
• Position 1 ATGCA = 0.15
• Position 2 TGCAA = 42.3
• Position 3 GCAAG = 0.18
P (i) = S / (∑ S)
Example 0.15 /(.15+42.8+.18)=0.003
P (1)= 0.003
P (2)= 0.993
P (3) =0.004
Building a PSSM for short motifs
• Collect all known sequences that bind a
certain TF.
• Align all sequences (using multiple
sequence alignment).
• Compute the frequency of each nucleotide
in each position (PSPM).
• Incorporate background frequency for each
nucleotide (PSSM).
Graphical Representation –
Sequence Logo
• Horizontal axis: position
of the base in the
sequence.
• Vertical axis: amount of
information (bits).
• Letter stack: order
indicates importance.
• Letter height: indicates
frequency.
• Consensus can be read
across the top of the letter
columns.
WebLogo - Input
• http://weblogo.berkeley.edu
WebLogo - Output
Genes:
Proteins:
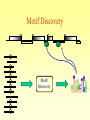
Finding new Motifs
• We are given a group of genes, which
presumably contain a common regulatory
motif.
• We know nothing of the TF that binds to the
putative motif.
• The problem: discover the motif.
Motif Discovery
Motif
Discovery
Example
Predicting the cAMP Receptor Protein (CRP)
binding site motif
Extract experimentally defined CRP Binding Sites
GGATAACAATTTCACA
AGTGTGTGAGCGGATAACAA
AAGGTGTGAGTTAGCTCACTCCCC
TGTGATCTCTGTTACATAG
ACGTGCGAGGATGAGAACACA
ATGTGTGTGCTCGGTTTAGTTCACC
TGTGACACAGTGCAAACGCG
CCTGACGGAGTTCACA
AATTGTGAGTGTCTATAATCACG
ATCGATTTGGAATATCCATCACA
TGCAAAGGACGTCACGATTTGGG
AGCTGGCGACCTGGGTCATG
TGTGATGTGTATCGAACCGTGT
ATTTATTTGAACCACATCGCA
GGTGAGAGCCATCACAG
GAGTGTGTAAGCTGTGCCACG
TTTATTCCATGTCACGAGTGT
TGTTATACACATCACTAGTG
AAACGTGCTCCCACTCGCA
TGTGATTCGATTCACA
Create a Multiple Sequence Alignment
GGATAACAATTTCACA
TGTGAGCGGATAACAA
TGTGAGTTAGCTCACT
TGTGATCTCTGTTACA
CGAGGATGAGAACACA
CTCGGTTTAGTTCACC
TGTGACACAGTGCAAA
CCTGACGGAGTTCACA
AGTGTCTATAATCACG
TGGAATATCCATCACA
TGCAAAGGACGTCACG
GGCGACCTGGGTCATG
TGTGATGTGTATCGAA
TTTGAACCACATCGCA
GGTGAGAGCCATCACA
TGTAAGCTGTGCCACG
TTTATTCCATGTCACG
TGTTATACACATCACT
CGTGCTCCCACTCGCA
TGTGATTCGATTCACA
Generate a PSSM
XXXXXTGTGAXXXXAXTCACAXXXXXXX
XXXXXACACTXXXXTXGATGTXXXXXXX
PROBLEMS…
• When searching for a motif in a genome using PSSM or
other methods – the motif is usually found all over the place
->The motif is considered real if found in the vicinity of a
gene.
• Checking experimentally for the binding sites of a specific
TF (location analysis) – the sites that bind the motif are in
some cases similar to the PSSM and sometimes not!
Computational Methods
• This problem has received a lot of attention from
CS people.
• Methods include:
– Probabilistic methods – hidden Markov models
(HMMs), expectation maximization (EM), Gibbs
sampling, etc.
– Enumeration methods – problematic for inexact motifs
of length k>10. …
• Current status: Problem is still open.
Tools on the Web
• MEME – Multiple EM for Motif Elicitation.
http://meme.sdsc.edu/meme/website/
• metaMEME- Uses HMM method
http://meme.sdsc.edu/meme
• MAST-Motif Alignment and Search Tool
http://meme.sdsc.edu/meme
• TRANSFAC - database of eukaryotic cis-acting regulatory DNA
elements and trans-acting factors.
http://transfac.gbf.de/TRANSFAC/
• eMotif - allows to scan, make and search for motifs at the protein
level.
http://motif.stanford.edu/emotif/