Download ppt - Avraham Samson`s Lab

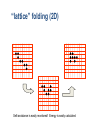
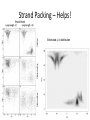
Structure prediction: Ab-initio
Lecture 9
Structural Bioinformatics
Dr. Avraham Samson
81-871
Let’s think!
Levinthal's paradox
In 1969, Cyrus Levinthal noted that, because of the very large
number of degrees of freedom in a polypeptide chain, the
molecule has an astronomical number of possible
conformations. For example, a polypeptide of 100 residues
will have 99 peptide bonds, and therefore 198 different phi
and psi bond angles. If each of these bond angles can be in
one of three stable conformations, the protein may misfold
into a maximum of 3198 (~10100) different conformations.
Therefore, a polypeptide would require a time longer than
the age of the universe to arrive at its correct native
conformation. This is true even if conformations are sampled
at rapid (picosecond) rates. The "paradox" is that most small
proteins fold spontaneously on a millisecond or even
microsecond time scale.
Protein Structure Prediction
• Two main categories of protein structure
prediction methods:
– Homology modeling (class of last week!)
– Ab-initio methods (class of today!)
• Methods can also be characterized:
– Based on physical principles (simulations)
– Based on statistics derived from known structures
(knowledge-based)
3
Secondary Structure Prediction
• Methods attempt to decide which type of
secondary structure (helix, strand or coil) each
amino acid in a protein sequence is likely to
adopt.
• The based methods are currently able to
achieve success rates of over 75% based on
sequence profiles.
4
Folding Simulations
• Accurate folding simulations will allow us to
predict the structure of any protein.
• However, this approach is impractical due to
limitations of computing power.
• Our understanding of the principles of protein
folding are far short of the level needed to
achieve this.
5
Homology Modeling
• Similar sequences
 Almost identical structures
• Sometimes referred to as “Comparative modeling”
• The most reliable technique for predicting protein
structure
• Comparing the sequence of the new protein with the
sequences of proteins of known structure
– Strong similarity (% identity, % similarity, alignment)
– No strong similarities  comparative modeling cannot be
used.
6
Predicting Small Conformational
Changes
• Native fold of a protein can be found
by finding the conformation of the
protein which has the lowest energy
as defined by a suitable potential
energy function.
• Even between very similar proteins, there are
differences.
• Some of these differences might be functionally
important (different binding loop conformations)
• Predicting what the effects of these small structural
changes is the real challenge in modeling
7
Ab initio Prediction
• Ab initio (i.e. ‘from scratch’)
• Use only the information in the target sequence
itself
• Two branches
– Knowledge-based methods
• Predict structure by applying statistical rules
• Rules: observations made on known protein structures
– Simulation methods
• Predict structures by applying physical parameters (Van-derWaals, dipole-dipole, etc)
8
Simulation Methods
• Most ambitious approach
• Simulate the protein-folding process using
basic physics
• Only useful for short peptides and small
molecules
• Very useful for predicting unknown loop
conformations as part of homology modeling
9
Energy Function
• Find a potential function
• Construct an algorithm capable of finding
the global minimum of this function
• The exact form of this energy function is as yet
unknown
• It is reasonable to assume that it would
incorporate terms pertaining to the types of
interactions observed in protein structures
– Hydrogen bonding
– Van der Waals effects
10
Searching Conformational Space
• Consider a protein chain of N residues
• The size of its conformational space is roughly 10N
states.
• 10 main chain
torsion angle triples
for each residue
• Not consider the
additional
conformational
space provided by
the side chain
torsion yet.
11
How to Find Global Energy Minimum
Efficiently
• Clearly proteins do not fold by searching their
entire conformational space (Levinthal’s
paradox)
• Proteins fold by means of a folding pathway
encoded in the protein sequence ?
• Short-chain segments (5-7 residues) could
quite easily locate their global minimum.
• Location of the native fold is driven by the
folding of such short fragments ?
12
One Subtle Point
• The native conformation need not necessarily
correspond to the global minimum of free
energy.
13
Secondary Structure Prediction
• Although predicting just the secondary
structure of a protein is a long way from
predicting its tertiary structure, information
on the locations of helices and strands in a
protein can provide useful insights as to its
possible overall fold.
• It is also worth noting that the origins of the
protein structure prediction field lie in this
area
14
Intrinsic Propensities for Secondary
Structure Formation
• Are some residues more likely to form -helices or -strands
than others?
• Yes
– Ex. proline residues are not often found in -helices
• 1974, statistical analysis of 15 proteins with known 3-D
structures
• For each of the 20 amino acids, calculate the probability of
finding any residue in -helices and in -strands
• Also calculate the probability of finding any residue in helices and in -strands
15
Example (Chou and Fasman, 1974)
• Suppose there was a total of 2000 residues in
their 15 protein data set
Total number of residues
Number of alanines
100
Number of helical residues
500
Number of alanines in helices

2000
50
We would calculate the propensity of alanine
for helix formation as follows:
P(Ala in Helix) = 50/500 = 0.1
P(Ala) = 100/2000 = 0.05
Helix propensity (PA) of Ala = P(Ala in Helix)/P(Ala) = 0.1/0.05 = 216
ab-initio prediction
• Prediction from sequence using first principles
AVVTW...GTTWVR
Ab-initio prediction
• “In theory”, we should be able to build native
structures from first principles using sequence
information and molecular dynamics
simulations: “Ab-initio prediction of structure”
– Simulation of the villin head piece (36-residues). (Pande et al.)
http://www.youtube.com/watch?v=1eSwDK
ZQpok&feature=related
http://www.youtube.com/watch?NR=1&v=
meNEUTn9Atg&feature=endscreen
... the bad news ...
• It is not possible to span simulations to the
“seconds” range
• Simulations are limited to small systems and
fast folding/unfolding events in known
structures
– steered dynamics
– biased molecular dynamics
• Simplified systems
typical shortcuts
• Reduce conformational space
– 1,2 atoms per residue
– fixed lattices
• Statistic force-fields obtained from known structures
– Average distances between residues
– Interactions
• Use building blocks: 3-9 residues from PDB structures
“lattice” folding (2D)
Self-avoidance is easily monitored! Energy is easily calculated
Example PROSA potential
Very stable
Low stability
Hydrophobic
C-C
Total
http://lore.came.sbg.ac.at:8080/CAME/CAME_EXTERN/ProsaII/index_html
Results from ab-initio
• Average error 5 Å - 10 Å
• Long simulations
Some protein from E.coli
predicted at 7.6 Å
(CASP3, H.Scheraga)
“loops” in homology modeling
Ab initio
PDB
Final test
• The model must justify experimental data (i.e.
differences between unknown sequence and
templates) and be useful to understand
function.
Rosetta energy function
•
•
•
•
•
Residue environment (solvation)
Residue pair interaction (electrostatic, disulfides)
Steric repulsion
Radius of gyration (vdw attraction, solvation)
Cb density (solvation, correction for excluded
volume)
• SS pairing (hydrogen bonding)
• Strand arrangement into sheet
• Helix-strand packing
Protein Structure Prediction using
ROSETTA
Worldwide distributed computing
Ab Initio Methods
• Ab initio: “From the beginning”.
• Assumption 1: All the information about the
structure of a protein is contained in its sequence
of amino acids.
• Assumption 2: The structure that a (globular)
protein folds into is the structure with the lowest
free energy.
• Finding native-like conformations require:
- A scoring function (potential).
- A search strategy.
Rosetta
• The scoring function is a model generated using
various contributions. It has a sequence
dependent part (including for example a term for
hydrophobic burial), and a sequence independent
part (including for example a term for strandstrand packing).
• The search is carried out using simulated
annealing. The move set is defined by a fragment
library for each three and nine residue segment
of the chain. The fragments are extracted from
observed structures in the PDB.
The Rosetta Scoring Function
Hydrophobic Burial
Residue Pair Interaction
The Sequence Independent Term
vector representation
Strand Packing – Helps!
Estimated f-q distribution
Sheer Angles – Help not!
Parameter Estimation
Parameter Estimation
Parameter Estimation
Parameter Estimation
Fragment Selection
Validation Data Set
CASP3 Protocol
Construct a multiple sequence alignment from f-blast.
Edit the multiple sequence alignment.
Identify the ab initio targets from the sequence.
Search the literature for biological and functional
information.
• Generate 1200 structures, each the result of 100,000
cycles.
• Analyze the top 50 or so structures by an all-atom
scoring function (also using clustering data).
• Rank the top 5 structures according to protein-like
appearance and/or expectations from the literature.
•
•
•
•
CASP3 Predictions
Why is Rosetta so fast?
Monte Carlo (Random Sampling)
http://www.chemistryexplained.com/images/c
hfa_03_img0571.jpg
• Randomly (or pseudorandomly)
pick a configuration and evaluate
its energy.
• If acceptably low, store result.
• If not, move a distance away
from that point as a function of
the energy (Metropolis criterion,
a.k.a. simulated annealing) and
evaluate again
• When some convergence
threshold or time limit is met,
stop and return stored results.
What have we learned?
• Can tackle sampling today
• Forcefields sufficient?
 Folding to the native state
 folding rate prediction
• Role of water
– Explicit solvent not crucial to rate determination?
– Compare to explicit solvent simulation
• Universal mechanism of folding?
– Maybe no universal mechanism: all proteins could be different?