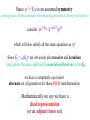Download SU(3) Multiplets & Gauge Invariance

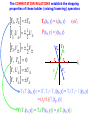
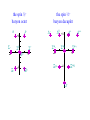
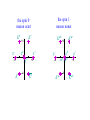
SU(2)
Combining SPIN or ISOSPIN ½ objects gives new states
described by the DIRECT PRODUCT REPRESENTATION
built from two 2-dim irreducible representations:
one 2(½)+1 and another 2(½)+1 yielding a 4-dim space.

ispin=1
triplet
+½
isospin
space
-½

=
=

which we noted reduces to 2  2 = 1  3

the isospin 0
singlet state
1
(
2
 -  )
SU(2)- Spin added a new variable to the parameter
space defining all state functions
- it introduced a degeneracy to the states already
identified; each eigenstaten became associated
with a 2+1 multiplet of additional states
- the new eigenvalues were integers, restricted to
a range (- to + ) and separated in integral steps
- only one of its 3 operators, J3, was diagonal,
giving distinct eigenvalues. The remaining
operators, J1 and J2, actually mixed states.
- however, a pair of ladder operators could
constructed: J+= J1 + iJ2 and J-= J1 - iJ2
which stepped between eigenstates of a given
multiplet.
-1/2
+1/2
-1
0
1
The SU(3) Generators are Gi = ½i
just like the Gi = ½i are for SU(2)
 0 1 0


1   1 0 0 
 0 0 0


 0 - i 0


2   i 0 0 
 0 0 0


 0 0 1


4   0 0 0 
 1 0 0


0 0 - i


5   0 0 0 
i 0 0 


 0 0 0


6   0 0 1 
 0 1 0


0 0 0 


7   0 0 - i 
0 i 0 


8
The ½ distinguishes
UNITARY from
 1 0 0


3   0 - 1 0 
 0 0 0


ORTHOGONAL
operators.
i appear in the
SU(2) subspaces
in block diagonal
3’s diagonal entries
form.
are just the eigenvalues
of the isospin projection.
1 3
0
0 


8   0 1 3
0 
 0

0
2
3


is ALSO diagonal! It’s eigenvalues must represent a NEW QUANTUM number!
Notice, like hypercharge (a linear combination of conserved quantities),
8 is a linear combinations of 2 diagonal matrices: 2 SU(2) subspaces.
The remaining matrices MIX states.
In exactly the same way you found the complete multiplets
representing angular momentum/spin, we can define
T±  G1± iG2
U±  G6± iG7
V±  G4± iG5
T±, T3 are isospin operators
 0 - i 0


2   i 0 0 
 0 0 0


By slightly redefining our variables
we can associate the eigenvalues of
8 with HYPERCHARGE.
Y (
2
)G8
3
(
 0 1 0


1   1 0 0 
 0 0 0


1
)8
3
 1 0 0


3   0 - 1 0 
 0 0 0


0
1 3 0

1
8   0 1 3 0
3
 0
0 -2




3
The COMMUTATION RELATIONS establish the stepping
properties of these ladder (raising/lowering) operators
T3 , T   T




1
T ,U   U 
3 
2
1
T3 , V   V
2
Y , T   0
Y , U    U 
Y , V   V
T3|t3, y = t3|t3, y
t3I3
Y |t3, y = y|t3, y
U+
Y
V+
T-
T+
V-
U-
I3
T3(T+|t3, y) = (T+T3+ T+)|t3, y = T+(T3+ 1)|t3, y
= (t3+1)(T+|t3, y)
Y (T+|t3, y) = T+(Y |t3, y) = y(T+|t3, y)
To be applicable to quantum mechanics,
the lowest dimensional representation of SU(3)
– the set of 3-dimensional matrices –
must act on, and their eigenvalues describe,
a set of real physical states,with quantum numbers:
 12

1
T3 =  3   0
2
0

0
-1
2
0
0

0
0 
ISO-SPIN I3
HYPERCHARGE
BARON NUMBER
STRANGENESS
CHARGE
Q = I3 + ½Y
Y=
+1/2
+1/3
+1/3
0
+2/3
0 
1 3 0


1
 8  0 1 3
0 
3
 0

0
2
3


0
-2/3
+1/3
-1
-1/3
-1/2
+1/3
+1/3
0
-1/3
Y  B+S
Since   U is an assumed symmetry
(mixing states within a multiplet but remaining invariant to strong interactions)
consider: 
* e-iaG**
which will also satisfy all the same equations as .
~
Since Gi = -(Gi)* are obviously also traceless and hermitian
(and satisfy the same algebraic Commutation Relations as the Gi)
we have a completely equivalent
alternate set of generators for these SU(3) transformations
Mathematically we say we have a
dual representation
(or an adjunct basis set).
Physically we interpret this as
another possible set of fundamental states
carrying the minimum quanta of
isospin and hypercharge,
though now the eigenvalues
(the diagonal elements of 3 and 8)
change signs.
+1
down
-1
Y
+1
up
s
+1
-1
strange
I3
-1
+1
u
-1
d
The anti-particle quarks!
As m strictly adds when combining | j1 m1 > | j2 m2 >
the quantum numbers t3 , y must as well.
+1
Y
down
up
-1
I3
+1
-1
This quark multiplet simply
plots the points representing
the 3 possible quark states.
strange
A 2-quark state of up pairs would
have a total t3=+1 and y=+2/3
+1
Y up/up
dn
+1
ud
up
-1
+1
-1
s
d
I3
Y
uu
u
-1
A ud state have a total
t3=0 and y=+2/3
+1
-1
s us
I3
The 33=9 possible quark-quark states form 33= 36 mulitplets
+1
Y
d
+1
+1
u
-1
+1
-1
s
I3
-1
+1
-1
-1
+1
-1
Unfortunately the 36 mulitplets of quark-quark combinations
include fractionally charged states,
which do not seem to correspond to any known particles.
But by adding a 3rd quark (to the qq states we’ve built so far):
+1
+1
-1
+1
-1
Which we can directly compare
to the known spin-1/2 baryons
to these
-1
+1
-1
63=18 qqq states
which can be separated into
63= 810 mulitplets
the spin 3/2+
baryon decuplet
the spin ½+
baryon octet
n
-
-
p
+1
0
+
0
-1
-
-1
+1
0
0
*-1
*-
+
+1
*0
++
*+
+1
*0
-1
-
Notice if you add a quark to an antiquark (or antiquark to a quark):
+1
-1
+1
+1
-1
-1
+1
-1
33=9 new states are defined, separable into 33= 18 mulitplets
to be compared directly to the known 9 spin-0 and 9 spin-1 mesons
the spin 0meson octet
the spin 1meson nonet
K0
K*0 +1
-
K+
+1
0
+
0
-1
K-
-1
+1
K0
-1
0
0, 0
K*-
-1
K*+
+
+1
K*0
1974 Accelerators 1st breached the NEXT energy threshold
and began creating NEW, HIGHER MASS particles!
Endowed with another quantum number:
requiring one more quark that carried it.
As we will see later, by this time theorists had already
extended u-d isospin symmetry
into an anticipated s-c symmetry
both subsets of larger SU(4) multiplets
c
d
u
s
-
+
0
0
+
+
-
0
n
+
p
++
Look at the FREE PARTICLE Dirac Lagrangian
LDirac=iħc gm m - mc2
Dirac matrices
Dirac spinors
(Iso-vectors,
hypercharge)
Which is OBVIOUSLY invariant under the transformation
eia
(a simple phase change)
because  e-ia
and in all
 pairings this added phase cancels!
This is just an SU(1) transformation, sometimes
called a “GLOBAL GAUGE TRANSFORMATION.”
What if we GENERALIZE this?
Introduce more flexibility to the transformation? Extend to:
eia(x)
but still enforce UNITARITY?
LOCAL GAUGE TRANSFORMATION
Is the Lagrangian still invariant?
LDirac=iħc gm m - mc2
m(eia(x)) = i(ma(x)) + eia(x)(m)
So:
L'Dirac = -ħc(ma(x)) gm m
+ iħce-ia(x)gm( m)e+ia(x) - mc2
L'Dirac =
-ħc(ma(x)) gm m + iħcgm( m) - mc2
LDirac
For convenience (and to make subsequent steps obvious) define:
- c
(x) 
then this is re-written as
a(x)
q
  e
- q / c
L'Dirac = +q gm m (m) + LDirac
recognize this????
the current of the charge carrying particle described by 
as it appears in our current-field interaction term

L'Dirac = +q gm m (m) + LDirac
If we are going to demand the complete Lagrangian
be invariant under even such a LOCAL gauge transformation,
it forces us to ADD to the “free” Dirac Lagrangian
something that can ABSORB (account for) that extra term,
i.e., we must assume the full Lagrangian
HAS TO include a current-field interaction:
L=[iħcgmm-mc2 -(qg m)Am
and that Am  Am +  m  defines its transformation
under the same local gauge transformation
L=[iħcgmm-mc2 -(qg m)Am
•We introduced the same interaction term 3 weeks back
following electrodynamic arguments (Jackson)
•the form of the current density is correctly reproduced
•the transformation rule
Am' = Am + m 
is exactly (check your notes!)
the rule for GAUGE TRANSFORMATIONS
already introduced in e&m!
The search for a “new” conserved quantum number shows that for an
SU(1)-invariant Lagrangian, the free Dirac Lagrangain is “INCOMPLETE.”
If we chose to allow gauge invariance, it forces to introduce
a vector field (here that means Am ) that “couples” to .
The FULL Lagrangian also needs a term describing
the free particles of the GAUGE FIELD (the photon we
demand the electron interact with).
We’ve already introduced the Klein-Gordon equation for
a massless particle, the result, the solution
A=0
was the photon field, Am

A (r , t )  
m
dk
3
(2 ) 2
3

ik r m
e s
(C e
1
+i t
+ C2e
-i t
Of course NOW we want the Lagrangian term that recreates that!
Furthermore we now demand that now be in a form
that is both Lorentz and SU(3) invariant!
)
We will find it convenient to express this term in terms
of the ANTI-SYMMETRIC electromagnetic field tensor
More ELECTRODYNAMICS: The Electromagnetic Field Tensor
• E, B do not form 4-vectors
but Am=(V,A) and
Jm=(c, vx, vy, vz) do!
• E, B are expressible in terms of m and Am
the energy of em-fields is expressed in terms of E2, B2
• Fm = mA-Am transforms as a Lorentz tensor!
F01   0 A1 - 1 A0 
F12  1 A2 -  2 A1 
 ( - Ax )
t
 ( - Ay )
x
-
-
V
x
 ( - Ax )
y
= Ex


since E  -V - A / t
= Bz


since B    A
Actually the
definition you
first learned:
F
0x
x A0

A
  A -  A  t - x
0 Ax
x 0
0 x

A
  A -  A  x - t  - F x 0
0 x
x 0
In general
F
0x
F
xy
 -F
x0
= -Ex
 -F
yx
= -Bz
F 00  F xx  etc = 0
Fik =
-Fki =
0
- Ex
Ex
0
- Bz
Ey
Bz
0
- Bx
Bx
0
Ez
- By
- Ey
While vectors, like Jm transform as J m  m J 

“tensors” simply transform as
m
m  

F
    F
- Ez
By

  
 
  

 m  m   0 ;     0 ,
,
,
x
 x
  x x y z 
 m  g m 




 
  

  0 ; -    0 , - , - , - 
xm  x
x
y
z 
  x
Under Lorentz transformations
x' =  x
or
x =
-1
m
m

( x )    x
x'

-1
x 
m

x
m
m


dx    dx

-1
dx  
m
dxm
dx
m

m
 
-1
dx  

dx
m
dx
m
So, simply by the chain rule:



x



 
 





x
x x
x
and similarly:


-1
  

x
x
 1 E 4 
 B +
 J

  E  4
xE x +  yE y + zE z 
4
c
c t
c
c
both can be re-written with
 x F x 0 +  y F y 0 +  z F z 0 + 0 F 00 
4
c
J0
 x F xx +  y F yx +  z F zx + 0 F 0 x 
4
c
Jx
(with the same for xyz)
All 4 statements can be summarized in
m F
m
4
 y B z -  z B y - 0E x  J x
c
(also xyzyzxzxy)
4 
 ( )J
c
  0, x, y, z

 B  0
 1 B
 E +
0
The remaining 2 Maxwell Equations:
c t
are summarized by
i F jk +  j Fki +  k Fij  0
ijk = xyz, xz0, z0x, 0xy
Where here I have used the “covariant form”
0
F = gm g
Fm =
- Ex
- Ey
- Ez
Ex
Ey
Ez
0
- Bz
Bz
0
- Bx
Bx
0
- By
By