Download Rational Numbers

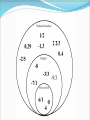
Numbers Sets
 Natural Numbers – Counting numbers.
Does not include 0 (example: 1,2,3,4…)
 Whole Numbers – All Natural numbers and
the number zero (example: 0,1,2,3,4…)
 Why is zero important?


Additive Identity – Any number added to zero
keeps it’s identity
Place Value – Holds a place when there isn’t a
quantity for that value
 Integers – All whole numbers AND THEIR
opposites (example: … -3, -2, -1, 0, 1, 2, 3…)
 Rational Numbers – Any number that can
be written in the form a/b where both a
and b are integers and b is not equal to
zero.
 In simple terms – all numbers that you
have ever dealt with EXCEPT NONterminating, NON-repeating decimals
(example: π )
Open and Closed Sets
 A set is a grouping of numbers (example: whole numbers,
integers, rational numbers, etc)
 A set is considered to be closed under an operation if the
result of the operation on two numbers in the set is another
member of the set
 Integer + Integer = Integer
ALWAYS TRUE
 Natural num + Nat. Num = Nat Num
ALWAYS TRUE
Therefore these sets are closed operations
Properties
 Additive Identity – A number such that when you add it to a
second number, the sum is equal to the second number
(example : 4 + 0 = 4)
 Multiplicative Identity – A number such that when you
multiply it by a second number, the product is equal to the
second number (example: 4 x 1 = 4)
 Additive Inverse – Two numbers are additive inverses if
their sum is the additive identity ( or 0)
(example: 3 + (-3) = 0 )
 Multiplicative Inverse – Two numbers are multiplicative
inverses if their product is the multiplicative identity (or 1)
(example: 5 x 1/5 = 1 )
 Commutative Property of Addition: Changing the order of two
or more addends in an addition problem does not change the sum
( a + b = b + a)
 Commutative Property of Multiplication: Changing the order
of two or more factors in a multiplication problem does not
change the product
(axb=bxa)
 Associative Property of Addition: Changing the grouping of
the addends in an addition problem does not change the sum
(a+b)+c=a+(b+c)
 Associative Property of Multiplication: Changing the grouping
of the factors in a multiplication problem does not change the
product
(axb)xc=ax(bxc)
Powers of Rational Numbers
 Power – a number written using a base and an
exponent
base
45=4x4x4x4x4
exponent
When calculating the power of a rational number
( ¾ )4 = 3 4 / 4 4
Operations with Powers
 Multiplication:
(1/4)2 x (1/4)3 = (1/4)2+3
(5)4 x (5)2 = (5)4 + 2
Add the exponents
 Division:
(1/4)4 ÷ (1/4)2 = (1/4)4 – 2
(5)4 ÷ (5)2 = (5)4 - 2
Subtract the exponents