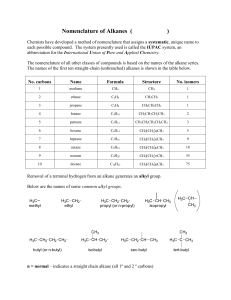
1 Introduction and Preliminaries
... (mod 4) and in this case we know that k · 2n + 1 splits as a product of two numbers of relatively equal size. There was not an analogous splitting situation for the k used to create Table 1. Before proceeding, we clarify that we are not suggesting that any of the remaining 8 values in the Seventeen ...
... (mod 4) and in this case we know that k · 2n + 1 splits as a product of two numbers of relatively equal size. There was not an analogous splitting situation for the k used to create Table 1. Before proceeding, we clarify that we are not suggesting that any of the remaining 8 values in the Seventeen ...
Section2.1notesall
... Solution: 25 11mod 7 since 7 evenly divides 25 – 11 = 14. Because of this, 25 and 11 are in the same congruence class. This is also true since 25 MOD 7 = 11 MOD 7 = 4, that is, they both give the same integer remainder MOD 7. In fact we can say that 32 25 18 11 4 mod 7 , that is, all of th ...
... Solution: 25 11mod 7 since 7 evenly divides 25 – 11 = 14. Because of this, 25 and 11 are in the same congruence class. This is also true since 25 MOD 7 = 11 MOD 7 = 4, that is, they both give the same integer remainder MOD 7. In fact we can say that 32 25 18 11 4 mod 7 , that is, all of th ...
PPT
... -- all numbers are positive, a 1 in the most significant bit just means it is a really large number signed (C declaration is signed int or just int) -- numbers can be +/-, a 1 in the MSB means the number is negative This distinction enables us to represent twice as many numbers when we’re sure that ...
... -- all numbers are positive, a 1 in the most significant bit just means it is a really large number signed (C declaration is signed int or just int) -- numbers can be +/-, a 1 in the MSB means the number is negative This distinction enables us to represent twice as many numbers when we’re sure that ...
There are infinitely many twin primes 30n+11 and 30n+13, 30n
... prove that the numbers X = 3n + 2 which are not generated by at least one of the formulas (37) to (46) are infinite. Given that the set of formulas (37) to (46)does not satisfy the proved proposition 4 which is a condition both necessary and sufficient, it follows that we can find infinitely some te ...
... prove that the numbers X = 3n + 2 which are not generated by at least one of the formulas (37) to (46) are infinite. Given that the set of formulas (37) to (46)does not satisfy the proved proposition 4 which is a condition both necessary and sufficient, it follows that we can find infinitely some te ...
Congruences
... power of an integer of our choice quite often. Note this statement can be proven easily by the repeated application of the method you used in Exercise 3, or more precisely, by using Induction. Have you ever wondered what is the use of "lame" properties like (a) in the last theorem? Well, read on. Th ...
... power of an integer of our choice quite often. Note this statement can be proven easily by the repeated application of the method you used in Exercise 3, or more precisely, by using Induction. Have you ever wondered what is the use of "lame" properties like (a) in the last theorem? Well, read on. Th ...
Standard
... Recognize the difference between rational and irrational numbers (explore different approximations of ) Place rational and irrational numbers (approximations) on a number line and justify the placement of the numbers Develop the laws of exponents for multiplication and division Write numbers in sci ...
... Recognize the difference between rational and irrational numbers (explore different approximations of ) Place rational and irrational numbers (approximations) on a number line and justify the placement of the numbers Develop the laws of exponents for multiplication and division Write numbers in sci ...