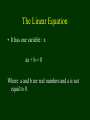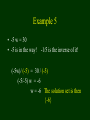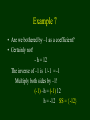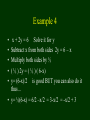* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download College Algebra Week 2
Survey
Document related concepts
Transcript
College Algebra Week 2
Chapter 2-3
The University of Phoenix
Inst. John Ensworth
This week we move on to
LINEAR EQUATIONS
• What is a linear equation?
• Why is it scary?
• It just means you have ONE variable in it,
and that variable isn’t squared or cubed or
anything crazy.
This kind of equation is your friend!
Section 2.1 Page 66
The Linear Equation
• It has one variable : x
ax + b = 0
Where a and b are real numbers and a is not
equal to 0.
A photo album of linear
equations
•
•
•
•
•
•
•
2x+3=0
x+8=0
3x=7
2x+5=9-5x
3+5(x-1)=-7+x
3=8x+5
Etc.
How to legally play with linear
equations.
• Most of the magic we work with are really
obvious tricks.
– Remember what happens if we multiply by
things that equal 1? e.g. 5/5 10/10 ?
• Adding the SAME THING to both sides of
an equation does not change the equation…
The Addition Property of
Equality
• So if you start with a = b
• You don’t change anything if you take a
new number or variable and add it to both
sides!
• a+c = b+c
The GOAL
• We want x all by itself on one side and the
rest of the junk on the other (so we can use
our calculator or fingers).
• The technical term for this is: solving for x
EXAMPLE 1 pg 66
• Solve x-3= -7
x–3=-7
x-3 + 3 = -7 + 3
x+0=-4
x= -4
The theme
• ISOLATE THE ‘X’ !!!
Then you can check your answer
• We got x = -4 so plug it into the first
equation:
• x- 3 = -7
• -4-3 = -7
• -7 = -7 CHECK!
Side note: {-4} is
solution set to the
equation.
EXAMPLE 2
• Solve 9 + x = -2
9+x=-2
9 + x – 9 = -2 –9
x + 0 = -11
x = -11
Solution set {-11}
Checking… 9 – 11 = -2 = -2 CHECK!
EXAMPLE 3
• Solve 1/2 = - 1/4 + y
(who cares if the variable is x or y or c or
whatever!)
1/2 = - 1/4 + y
1/2 + 1/4 = -1/4 + y + ¼
2/4 + 1/4 = y + 0
3/4 = y
S.S. {3/4}
Checking ½ = - ¼ + ¾ = 2/4 = ½ = ½ check!
The next trick…multiplication
• That is nice if the stuff we want to move to
the non-x side is just added or subtracted
from the ‘x’, but what if the number is a
coefficient of ‘x’? What if it looks like
3x= 9 ?!
The multiplication property of
equality
• If, again, you have a equation like
a=b
And you multiply both sides by c, then you
haven’t changed the equation!
ac=bc
Again, c can’t be 0.
EXAMPLE 4
• Solve x/2 = 6
Note, you can’t subtract or add anything
to get x by itself.
So multiply both sides by 2! (Which is the
INVERSE of the offending number).
2*x/2 = 2*6
2/2 * x = 12
x = 12 SS = {12}
A quick check…
• Plugging 12 into x/2 = 6
– 12/2 = 6 = 6 good thing!
Example 5
• -5 w = 30
• -5 is in the way! -1/5 is the inverse of it!
(-5w)/ (-5) = 30 / (-5)
(-5/-5) w = -6
w = -6 The solution set is then
{-6}
EXAMPLE 6
• Fractions as coefficients aren’t a problem
either!
• 2/3 p = 40
• 2/3rd offends, kill it with 3/2nd
(3/2) * 2/3 p = 40 * (3/2)
1 * p = (40*3)/2 = 20*3 = 60
p = 60 our solution set is {60}
Example 7
• Are we bothered by –1 as a coefficient?
• Certainly not!
- h = 12
The inverse of –1 is 1/-1 = -1
Multiply both sides by –1!
(-1) –h = (-1) 12
h = -12 SS = {-12}
Example 8
Sometimes things are messier…
• What if you have a more goofed up
equation?
-9 + 6y = 7 y
There are dumb y’s on both sides… so first we
need to get the y’s on ONE side, THEN do
what is needed to get y alone.
-9 + 6y –6y = 7y – 6y
-9 = y !
Wow, the solution set is there … {-9}
Set to Exercises 2.1
• Go to the section you have the hardest time
working with
–
–
–
–
–
–
Definitions Q 1 –6
Solving equations with + and - Q 7 – 30
Solving equations with * and / Q 31 – 54
Doing it with –1 in play Q 55 – 62
Solving it with x on both sides Q 63 – 70
Random mix of anything Q 71 - 90
Section 2.2
• Now we graduate to equations that need
both addition/subtraction and
multiplication/division in the same solution.
• Not a problem… right?
Rules for Happiness
• First do whatever adding and subtracting
you can do…
• THEN do whatever multiplication and
division you can do.
• THEN you should be done!
Example 1
• Solve 3r – 5 = 0
• Step one… addition or subtraction?
3r –5 + 5 = 0 + 5
3r = 5
• Step two … division or multiplication?
(1/3) 3r = (1/3) 5
r = 5/3
Our solution set is {5/3}
Example 2
• Solve -2/3 x + 8 = 0
-2/3 x + 8 – 8 = 0 – 8
-2/3 x = - 8
Mult/Div.: (-3/2) –2/3 x = (-3/2) (–8)
1*x = (-3)(-8)/2
x = (-3)(-4) = 12
Our solution set is {12}
Checking: (-2/3) (12) + 8 = -24/3 + 8 = -8 + 8 = 0 check
Add/Subt. :
Example 3
Now with x’s elsewhere and +&- *&/
• Solve 3w –8 = 7w
• Group the variable’s
3w –8 –3w = 7w –3w
-8 = 4w
• What’s needed? Get ride of that 4 sticking
to the w!
-8 (1/4) = (1/4) 4w
-8/4 = w
-2 = w Our Solution set = {-2}
Example 4
• Solve ½ b – 8 = 12
• Add 8 to both sides first
½ b – 8 + 8 = 12 + 8
½ b = 20
• THEN multiply both sides by the inverse of ½ .
Which is 2!
2* ½ b = 2 * 20
b = 40
Our solution set is {40}
CHECK it… ½ (40 ) – 8 = 20 – 8 =12 = 12 CHECK!
Example 5 - a tad bit more
complex
•
•
•
•
The form NOW is ax+b=cx+d
No big change…
Addition first and get the x’s together then proceed
Solve 2m-4=4m-10
2m -4m –4 = 4m –4m –10
-2m -4 = -10
-2m -4 +4 = -10 +4
-2m = -6
(- ½ ) –2m = (- ½ ) (-6)
m=3
Our solution set is {3}
Checking it…
•
•
•
•
2m-4=4m-10 and m=3 right?
2(3) –4 = 4(3) –10
6 –4 = 12 –10
2 = 2 YES!
Stepping back in time…
Example 6
• Remember expanding stuff? (Chapter 1)
You MAY need to do it FIRST, then solve for
x.
We’ll work with 2(q-3) +5q = 8(q-1)
On the next slide…
Workin’ on the railroad
2(q-3) +5q = 8(q-1)
First multiply the parenthesis out, then do the normal
stuff…
2q-2(3) + 5q = 8q –1(8)
2q –6 + 5q = 8q –8
Combine the q’s on the right : 7q –6 = 8q –8
Then subtract 7q from both sides
7q –7q –6 = 8q – 7q – 8
-6 = q –8
Then add 8 to both sides -6 +8 = q –8 +8 give us
2 = q Our solution set is {2}
Don’t forget to check it later!
Cook Booking It
1. Remove parentheses and combine like terms on
each side
2. Use addition property to get like terms on the
same side as each other (things with x on one
side, numbers only on the other)
3. Use the multiplication property to get the x
alone
4. If x is negative, use the –1 multiplication trick to
make x positive
5. Check your solution to see if you got it!
Section 2.2 Exercises
• Do the hardest first!
–
–
–
–
–
Definitions Q 1-4
Simple one variable solutions Q 5 – 20
One variable but on both sides Q 21- 44
Multiply out first… Q 45 – 52
Numbers and variables on both sides Q53-90
Section 2.3 Equations with more
than one simple answer (or no
answer)
• Identities = stupid equations in which all
numbers are the answers
x/2 = ½ x
x=x
x+x = 2x
3x + 3 = 3(x+1)
x+1 = x+1
yadda yadda
5/x = 5/x (note x can’t equal 0)
Is it an identity?
• Simplify both sides…
Example 1 7-5(x-6)+4=3-2(x-5)-3x+28
Kill the ()’s 7-5x+30+4=3-2x+10-3x+28
Group like stuff -5x+41 = -5x+41 Hurray!
Another definition
• A Conditional Equation
• Is ANY equation that has at least one real
answer (or more) but is NOT an identity
• Everything we’ve done so far is an example
of a Conditional Equation
• Another example x2=4 2 and –2 both
work. (Solution set = {2,-2} )
And another definition
• Inconsistent Equations
• They have NO answer.
x=x+1 x-x = x-x+1 0 = 1 Woa! Yikes!
0 * x + 6 = 7 0 + 6 = 7 6 = 7 Buzz.
Etc.
Finding an inconsistent equation
• Example 2 Solve 2-3(x-4)=4(x-7)-7x
2- 3x+12 = 4x –28 –7x
-3x + 14 = -3x –28 Hey! That can’t be!
one more step -3x +3x + 14 = -3x +3x –28
14 = -28 Nope, it’s just off.
And now for another
combination… least common
denominators making life easier
• It seems a bit out of place, but let’s combine
what you learned about LCD’s and
simplifying equations… it IS a good thing.
• Example 3 …
A bit of forethought makes things
smoother
• Solve y/2 –1 = y/3 + 1
• We know that we will eventually have to
add the y terms together. But they have
different denominators.
• We know that 2*3 = 6 will give us a
common denominator. So let’s multiply
both sides by 6 first!!!
Common denominators
•
•
•
•
•
•
•
y/2 –1 = y/3 + 1
6(y/2-1) = 6(y/3+1)
Expand (6/2) y –6 = (6/3)y +6
3y –6 = 2y + 6
Next 3y –2y –6 = 2y –2y +6 y-6=6
y-6 + 6 = 6 + 6 y = 12 SS = {12}
Checking: 12/2-1 =? 12/3 + 1 6-1
=?4+1 5=5 Cool!
What if you have decimals?
Break out the calculator.
• Nothing new here, the numbers just look a
bit different.
• Solve 0.3p + 8.04 = 12.6
• 0.3p+ 8.04 –8.04 = 12.6 – 8.04
• 0.3p = 4.56
• (1/0.3) 0.3 p = (1/0.3) 4.56
• p= 15.2
The Solution Set is {15.2}
The same problem multiplying
by 10, 100, 1000 or something
like that
• Solve 0.3p + 8.04 = 12.6
• Note that the greatest number of places to the right
of a decimal place is 2 which can be erased if we
multiply by 100
• So 100(0.3p + 8.04) = 100(12.6)
• 30p + 804 = 1260 subtract 804 from both sides
• 30p = 1260 – 804 = 456 then divide by 30
• (1/30) 30p = (1/30) 456
• p= 15.2 THE SAME ANSER!
Another with helpful factors of 10
•
•
•
•
•
•
•
•
•
Solve 0.5x + 0.4(x+20) = 13.4
Expand 0.5x + 0.4x + 8 = 13.4
Combine 0.9x + 8 = 13.4
X 10 kills all decimals
10(0.9x +8) = 10(13.4)
9x + 80 = 134
9x = 134 – 80 = 54
9x= 54 divide both sides by 9
x= 6
The solution set = {6}
Practice section 2.3!
• Do it do it do it!
– Definitions Q 1-6
– Looking for conditional equations, inconsistent
equations or identities Q 7 – 26
– Killing fractions with LCD’s Q 27- 38
– Decimals Q 39 – 52
– Anything goes mixed bag Q 53- 86
On to Section 2.4 Formulas
• Don’t be fooled, this isn’t any harder except
we sometimes don’t have ANY obvious
numbers… we have letters and we choose
one variable to be OUR variable for
solving.
• You just leave the answer with the letters
however they fall… but the tricks are all the
same as what we have already used.
The trick…
• Pretend all the OTHER variables are just
numbers to get out of the way.
Definition
• A formula or literal equation is an equation
involving two or more variables. We solve
it for a certain variable.
• Making formulae work for us is a main
reason to even worry about solving for any
particular variable! This can be useful!
Example 1
• Solve D=RT for T…
• D/R = (R*T)/R divide both sides by R to
get T alone
• D/R = T
• Swap sides T = D/R done!
Example 2
•
•
•
•
•
•
•
•
The Celsius to Fahrenheit equation…
C = 5/9 ( F –32) for F
We need to get rid of the 5/9 with 9/5
(9/5) C = (9/5) (5/9) (F-32)
(9/5) C = F-32 then add 32 to both sides
9/5 C + 32 = F (-32 + 32)
9/5 C + 32 = F switch sides
F= 9/5 C + 32 done!
Example 3
• Solving for x when it’s on both sides
(you’ve already done this) but now you
have some other letters going along for the
ride like numbers.
Example 3
•
•
•
•
•
•
5x – b = 3x + d subtract 3x from both sides
5x –3x -b = d 2x –b = d
Add b to both sides
2x = d + b
Divide both sides by 2
x= (d+b)/2
done!
Note on speed…
• Note, I’m dropping some steps in solving
equations that you should be getting
smoother at. I’m labeling the steps, but not
showing ever tiny part.
Example 4
•
•
•
•
•
x + 2y = 6 Solve it for y
Subtract x from both sides 2y = 6 – x
Multiply both sides by ½
( ½ ) 2y = ( ½ ) ( 6-x)
y= (6-x)/2 is good BUT you can also do it
thus…
• y= ½(6-x) = 6/2 –x/2 = 3-x/2 = -x/2 + 3
Example 5
• Solve 2x-3y = 9 but make it look like y=mx+b
(the slope of a line, to be used a LOT later!).
m and b are what ever numbers they turn out to
be.
• We want y alone on the left… so subtract 2x
from both sides.
• -3y = 9-2x Then divide both sides by –3
• y = 9/(-3) – 2x/(-3)
• y= -3 + (2/3)x then swap the number and the
x
• y= (2/3)x –3 looks like y= mx+b m=2/3, b=-3
Finding the value once you’ve
solved the equation
• In example 5 we found that 2x-3y-9
becomes y= (2/3)x –3
• If we’re told that x=6, what is y?
• y= (2/3) 6 –3 = 12/3 – 3 = 4 –3 = 1
• That means on this line (more on that later)
if x = 6 then y = 1.
Example 7 The simple interest
formula
Solve I=Prt You know the simple interest
$120 (I), the principle is $400 P) over 2
years (t). What is the rate (r) ?
Prt = I divide both sides by P and t
Prt/(Pt) = I/ (Pt)
r= I/Pt = 120/(400*2) = 0.15 or 15%
fun no?
Example 8
• How about using the perimeter equation for
a rectangle? What is the Length (L) if the
Perimeter (P) is 36 feet and the width (W) is
6 feet?
• P=2L+2W
• P-2W= 2L
• 2L= P-2W divide by 2
• L= (P-2W)/2 = (36-2(6))/2 = 12 feet
Section 2.4 Formula Practice
• Give ‘em a test drive…
–
–
–
–
–
–
Definitions again Q1 – Q 6
Working with formulae Q 7 – 24
Letters instead of numbers in equations Q 25-32
Making things look like y=mx+b Q 33- 50
The same thing but with x=2 Q 51-60
Working with word problems of all the above
• Q 61- 87 USEFUL!
Section 2.5 – Putting this into
words
• This is the last section in Chapter 2 (then we
hop to 3.1-3.3)
• This section expands on the verbal work
you did in 1.6
Verbal Phrases… Math as a
language again… Addition first
• Addition:
–
–
–
–
The sum of a number and 8
Five is added to a number
Two more than a number
A number is increased by 3
x+8
x+5
x+2
x+3
More talk - Subtraction
• Subtraction
–
–
–
–
Four is subracted from a number
x-4
Three is less than a number
x-3
The difference between 7 and a number x-7
A number is decreased by 2
x-2
Multiplication
• Multiplication
–
–
–
–
The product of 5 and a number
Twice a number
One half a number
Five percent a number
5x
2x
½x
0.05x
Division
• Division
– The ratio of a number to 6
– The quotient of 5 and a number
– Three divided by some number
x/6
5/x
3/x
Algebraic Expressions in Words
• Example 1
–
–
–
–
–
The sum of a number and 9
x+9
Eighty percent of a number
0.80w
A number divided by 4
y/4
The result of a number subtracted from 5 5-z
Three less than a number
a-3
Adding wording for pairs of
numbers
• If you sort of know how two numbers are
related to one another, then you can
construct one of those equations we’ve
worked with that has two x’s in it.
• Like addresses… “that house is three
houses down the street from this house.”
And I know the address of this house, so I
can figure out the other house’s number.
I know…
• I have two numbers… one number is 10
less than the other…
• I can write the first number as x
• And the other is 10 more than it, then it is
x+10
Example 1
• Write two numbers that differ by 12
x and x-12
Check x – (x-12) = x-x+12 = 0 +12
• Two numbers with a sum of –8
x and -8-x
Check x+ (-8-x) = x-x-8 = 0 –8 = -8
The trick, write down x. Write down the answer +
the opposite of the variable x (-x). Then show if
you are adding or subtracting the values.
Example 2
A related subject
• If you know the overall angle in some
geometric shape…you can do this same
‘two things added’ verbal trick.
• But now we know the overall angle!
Ex 2 continued
• See page 96… a)
• The right angle has 90 degrees. Fact.
• A smaller angle that is x and is part of the
overall 90 degree angle. The rest of the
stuff in that 90 degree angle is ?. So the
remainder is 90 – x or ? = 90-x
• Nutty simple? If not, you are overthinking!
Ex 2 b and c
• (b) So if you have in (b) 180 degrees and a
smaller part of that called x. Then the rest
of the stuff in the 180 degree angle is 180-x
• (c) The interior angles of all triangles equals
180 degrees. So if you know one angle (30
degrees) and another angle is x, then the rest
of it is: 180 –x –30 or 150 – x
Yet another in the same vein…
•
Example 4 - describing sets of numbers
a) Write three consecutive integers, the smallest
of which is w
w, w+1, w+2
b) Write three consecutive even integers, the
smallest of which is z
z, z+2, z+4
MORE Writing
• How about using known formulae?
– Example 5 a
– The distance if the rate is 30mph and the time is
T hours
– We go find the formula D=RT for
distance=rate times time
– Plug in the known value… R=30mph
– So D=30T
done!
Example 5b
• The discount rate if the rate is 40% and the
original price is p dollars
• We go get the formula
Discount = Rate of discount * Original
Price
• Since the discount is the rate times the
original price, an algebraic expression for
the
discount = 0.40p dollars
Page 97 is your repository of
equations for these problems!
• See this page for many normal, everyday
formulae.
• Use these for the quizzes and all!
Example 6 Words and Formulae
• a) Find two number that have a sum of 14
and a product of 45
• First, x is one of the numbers. Just say it.
• The other number is 14-x (the answer and
the opposite of the first number)
• Their product is 45 : x(14-x) =45 done!
Ex 6b
• The coat is on sale for 25% off the list price. If
the sale price is $87, then what is the list price?
• Our variables. x is the origional price (just say it)
The amount of discount is 0.25x
• Which formula on pg 97?
Original price – discount = selling price (the third
one)
• Plug it in: x –0.25x = 87 done!
Example 6c
• What percent of 8 is 2?
• If x is the percentage, then we want to
know the ratio 2/8
• x=2/8 or 8x = 2
• Don’t forget to multiply the answer by 100
to make it a percent in the end.
Example 6d
• The value of x dimes and x-3 quarters is $2.05
• We’ll say the value of x dimes at 10 cents each is
10x cents.
• The value of x-3 quarters at 25 cents each is 25(x3)
• The sum of them is 10x+25(x-3) = 205
(the $2.05 was turned into cents as well! Unit must
match!)
Work on Section 2.5 Questions
for a bit!
• Go for the hardest first and get help!
–
–
–
–
Definitions Q1 to Q6
Translating words to equations Q 7 to 30
Playing with the same idea but with angles Q31 to 33
Words describing sets of numbers to expressions Q 35 to
42
– Words describing expressions to expressions Q 43-66
– Words describing equations to equations Q67 - 96
CHAPTER 3
All the same things with
inequalities instead of = signs
• It’s a shift in what ‘equals’ means.
• This allows you to practice all the tricks and
games you’ve learned so far.
• Remember the number line?
– Is
–5 greater or less than 4?
• But it starts with some new definitions…
3.1 Inequalities
• The Basics
•
•
•
•
< Is less than
=! Is not equal to
<= Is less than or equal
> Is greater than
>= Is greater than or equal to
We are comparing numbers
(or sides of an expression)
• We are comparing them then asking if it is
true or not (much of the time).
• True or false? -10 < -5
Example 1
•
•
•
•
a)
b)
c)
d)
is
is
is
is
-5 < 3 ? True
-9 > -6 ? False
-3 <= 2 ? True
4 >= 4 ? True
We can mark it on the number
line!
• Remember the solution set? We put the
answer in { }’s
• Any solution set can be written on the
number line
• For instance, All x’s such that x is less than
three… {x|x<3}
Note the “ ) “
Another example
• This is the number line graph all x’s such
that x is greater OR equal to 1.
• {x|x>=1} Note the “ [ “ this time for the
equal
Watch the (‘s and [‘s and the way
they point.
The basic number line again
----|----|----|----|----|----|----|----|----|----|----|----5 -4 -3 -2 -1 0 1 2 3 4 5
Example 2
• a)
• x > -5
----(----|----|----|----|----|----|----|----|----|----|--->
-5 -4 -3 -2 -1 0 1 2 3 4 5
Example 2b
• b)
• x<=2
<---|----|----|----|----|----|----|----]----|----|----|----5 -4 -3 -2 -1 0 1 2 3 4 5
Solving Linear Inequalities
The official properties…
• If you multiply both sides of an inequality by a
negative number you must switch the inequality sign
In SIMPLE terms
• All the rules are the same as you worked
with equalities EXCEPT if you multiply or
divide by a negative number
• Multiply or divide by a negative number
and you switch the > to a < or the reverse.
Example 3 Seeing how it
works…
• a) 2x –7 < -1
2x-7 +7 < -1 + 7
2x < 6
(1/2) 2 x < (1/2) 6
x < 3 or {x|x<3}
Example 3b
•
•
•
•
•
•
5- 3x < 11
5 –5 –3x < 11 –5 -5 both sides
-3x < 6
(-1/3) 3x < (-1/3) 6 * -1/3 both sides
x > -6/3 = -2 SWITCHED < to >
x > -2 or {x|x > -2}
Example 4
• (8+3x)/-5 >= -4 simplify and graph
• So we solve for x again… NOTHING NEW (except
watching for that multiply by –1 thing)
• (-5)*(8+3x)/(-5) <= -4 * (-5) so we do it first!
and switch the inequality
•
•
•
•
•
8+3x <= 20
3x <= 20-8 (subtract 8 from both sides)
3x <= 12
finish the right side
x <= 12/3 divide both sides by 3
x <= 4
graph on next page…
Ex 4 continued
x <= 4
<---|----|----|----|----|----|----|----|----|----]----|----5 -4 -3 -2 -1 0 1 2 3 4 5
•
•
•
•
•
•
•
•
•
•
Example 5 now with fractions for more flavor!
1/2 x – 2/3 <= x+ 4/3
If we multiply the whole thing by the least common
denominator ( 2*3=6) then life will be so so so so much
more easy
And remember, you trained for this moment!
6(1/2x – 2/3) <= 6(x+ 4/3)
6/2 x - 12/3 <= 6x + 24/3 no switch of the <=
3x – 4 <= 6x + 8
3x-6x –4 <= 8 subtract 6x from both sides
-3x <= 8+4 add 4 to both sides
x >= 12/-3 divide by –3 and switch the inequality
x >= -4
Graphing Ex 4
• X >= -4
---|----[----|----|----|----|----|----|----|----|----|--->
-5 -4 -3 -2 -1 0 1 2 3 4 5
We’ll skip the 2nd half of 3.1 and
go right to part of the exercises
•
•
•
•
•
•
•
•
How do you get to Carnegie Hall?
Do Inequalities…
Definitions Q 1 – Q 6
True or False – the Game Q 7 – Q 20
Write and graph it Q 21 – 28
Use that alternate notation pg 123 Q 29-36
Supply the <, <=,>, >= Q37-44
Solve and Graph (like examples) Q 45 -72
Section 3.2 The next step with
inequalities
• We take two simple inequalities (section
3.1) and link them with “and” or “or”.
• We can use simple logic…
• We can defined a range!
Example 1 True or False? AND
• a) 3>2 and 3 < 5
• The first one is true, the second one is true
• True AND true = true
• b) 6> 2 and 6<5
• The first one is true, the second is false
• True AND false = false
Example 2 True or False? OR
•
•
•
•
a) 2 < 3 or 2 > 7
The first is true, the second is false
BUT if ONE is true with an OR, it is true
True OR False = True!
b) 4<3 or 4 >= 7
• The first is false and the second is false
• False OR False = False! (there isn’t any truth here
at all)
Example 3 True or False –
testing a number
• a) x <6 and x < 9 we’ll test 5
• 5 < 6 and 5 < 9
• True and True = True!
•
•
•
•
b) 2x-9 <= 5 or -4x >= -12 plug in 5…
10-9 <= 5 or –20 >= -12
1 <= 5 or -20 >= -12
True or False = True (One true is enough with OR)
Graphing those compound
inequalities
• The trick is to lightly sketch ONE inequality
then the OTHER then , depending on the
AND or OR, combine them to make the
answer…
• Definitions: The intersection of two sets is
the set of all numbers both sets share.
Intersections
• A intersects B is written as
A ‘upside down U’ B
( I can’t reliably make an upside down U here… sorry)
•
•
•
•
A = { 1,2,3} and B = {2,3,4,5}
Then A “upside down U” B = {2,3}
That’s all they share, that’s all that intersects
This is the AND of sets
Ex 4 – Graphing them
• x > 2 and x < 5
----|----|----|----|----|----|----|----(----|----|----|-->
-5 -4 -3 -2 -1 0 1 2 3 4 5
<--|----|----|----|----|----|----|----)----|----|----|----2 -1 0 1 2 3 4 5 6 7 8
----|----|----|----(----|----|----)----|----|----|----|----1 0 1 2 3 4 5 6 7 8 9
The Union
•
•
•
•
•
•
The Union of two sets is the same as OR.
It is the set of all numbers in A OR B
We write A U B
If A = {1,2,3} and B = {2,3,4,5}
Then A U B = {1,2,3,4,5}
It’s ALL of them!
Graphing them… Ex 5
• x > 4 or x < -4
----|----|----|----|----|----|----|----|----|----(----|-->
-5 -4 -3 -2 -1 0 1 2 3 4 5
<--|----)----|----|----|----|----|----|----|----|----|----5 -4 -3 -2 -1 0 1 2 3 4 5
<--|----)----|----|----|----|----|----|----|----(----|-->
-5 -4 -3 -2 -1 0 1 2 3 4 5
Doing it quicker, Ex 6
• a) If we are given x<3 and x < 5 we need
only shade what is less than 3 (where they
overlap)
<--|----|----|----|----)----|----|----|----|----|----|----1 0 1 2 3 4 5 6 7 8 9
Ex 6b
• b) x>4 or x>0 shade everything since it’s OR
----|----|----|----|----|----(----|----|----|----|----|--->
-5 -4 -3 -2 -1 0 1 2 3 4 5
All or nothing
• Sometimes the set just includes every
number on the number line and sometimes
there are NO numbers that satisfy the
intersection
Example 7 a) x< 2 and x >6 No
Intersection
b) x<3 or x> 1 ALL NUMBERS are the
answer
Back to solving first…
• Sometimes you need to solve the inequality
like we did in 3.1 …
• Example 8 x+2 > 3 and x-6 < 7
• Step 1, get x alone x>1 and x<13
subtract 2 from both sides
add 6 to both sides
----|----(----|----|----|----|----|----|----|----|----|----|----|----)----|----|----
0
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15
Ex 9 solving with a Union
•
•
•
•
5-7x >= 12 OR 3x –2 < 7
Solve for x
-7x >= 7 OR 3x < 9
x<= -7 OR x<3 (switched inequality!)
<--|----|----|----|----|----|----|----|----)----|----|----5 -4 -3 -2 -1 0 1 2 3 4 5
Compacting the Trash
• We read these things with the variable first
(the brain likes it that way)
• So 1< x reads “x is greater than 1”
(and is also x>1)
• With intersections (AND) we can compact
things a bit more
• Why write x >1 and x <13 when this is better:
• 1 < x < 13 “Called a compound inequality”
Other legal compounds
• You can use < < and > > and >= >= and <=
<= but not < >
• 4<x<9
• -6 >= x >= -8
• 10 > x > 2
• But NOT: 5 < x < 2 or 5 < x > 7
Ex 10 Compounding your
troubles
•
•
•
•
•
-2 <= 2x –3 < 7
Solve for x
-2 +3 <= 2x < 7 +3 (+3 to all parts)
1 <= 2x < 10
½ <= x < 5
(multiply ½ to all parts)
----|----|----|----|----|----|--[--|----|----|----|----)----5 -4 -3 -2 -1 0 1 2 3 4 5
A fable problem Ex 11
• Fiana is getting a grade from 2 scores in a
class. Her midterm was a 76 and her final is
unknown (x). She can get a B if she is
between 80 and 89 in the end. What scores
can she get to earn a B?
Ex 11 continued
•
•
•
•
80<= (x+76)/2 <= 89
160 <= x+76 <= 178 ( mult. all parts by 2)
84 <= x <= 102 (subt. 76 from all parts)
That’s the range (can she get extra credit for
the 102?). What color was her sweater?
Section 3.2 hoops to jump
through
•
•
•
•
•
•
•
Definitions Q 1 to 6
Compound True or False Q 7 to 18
Graph given compound inequalities Q19-30
Solve THEN graph compound ineq. Q31-52
Working with the short ( ) notation Q53-66
Going from graph to inequality Q67-78
Solve and write in short ( ) notation Q77-82
Section 3.3 All the fun WITH
absolute values now…
• |x|=5 The solution set is {-5,5}
• |0| = 0 which is {0}
• |x| = -7 is an empty set (no answer with real
numbers)
Example 1 positive numbers
•
•
•
•
a) |x-7| =2
First: Take away the | |’s (it gives us 2 answers!)
x-7 = 2 or x-7=-2 (Just like –5, 5 above)
x=9 or x =5 so our solution set is {5,9}
Example 1b
• b) |3x-5| = 7
• First: 3x-5 = 7 or 3x-5 = -7
3x=12
or 3x = -2
x= 4 or x = -2/3 our solution set is {-2/3, 4}
Example 2 Now with 0
• |2(x-6)+7| = 0
• We have only 1 answer, 0
• 2(x-6) + 7 = 0
2x-12+7=0
2x-5=0
2x=5
x=5/2 The solution set is {5/2}
Example 3 now with a negative
answer
• -5|3x-7| + 4 = 14
• -5|3x-7| = 10
• |3x-7| = -2
• Buzzzt. No answer in the Real World.
Example 4 Can we have ||’s on
both sides?
• Sure! We’re just crazy enough!
Example 4
•
•
•
•
•
•
|2x-1| = |x+3|
First, kill the ||’s
2x-1 = x+3 or
2x=x+4
or
2x = x+4
or
x= 4
or
2x –1 = -(x+3)
2x= -x -3 +1
2x = -x –2
3x = -2
x = -2/3 SS {-2/3,4}
Absolute values are HIDDEN
inequalities… believe that?
• |x| > 5
• Is the same as x >5 or x < -5
----|----|----|----)----|----|----|----|----|----|----|----|----|----(----|----|----|----8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
And a < is like an AND
• |x| <= 3
• -3 <= x <= 3
----|----|----|----|----|----[----|----|----|----|----|----]----|----|----|----|----|----8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Example 5
•
•
•
•
|x-9| < 2 (Less than is like AND)
This is like –2 < x –9 < 2
Solve for x -2 +9 < x < 2 + 9 (+9 to all parts)
7 < x < 11
----|----|----|----|----|----|----|----|----|----(----|----|----|----)----|----|----|-----2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Example 6
•
•
•
•
|3x+5| >2
3x+5 > 2
3x> -3
x > -1
(greater than is like OR = Outside)
OR 3x+5 < -2
or 3x < -7
or x < -7/3
<---|----|----|----|----|----|---)-|----(----|----|----|----|----|----|----|----|----|--->
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Example 7 Another < (AND)
• |5 –3x| <= 6
-6 <= 5-3x <= 6
-11 <= -3x <= 1
-11/3 >= x >= -1/3
SS = {-1/3,11/3}
subtract 5
divide by 3
----|----|----|----|----|----|----|----|--[-|----|----|----|--]-|----|----|----|----|----8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Example 8 Special 0 (not K)
• 3+ |7-2x| >= 3
• |7-2x| >= 0
• BUT ALL real numbers you can plug in
work because the ||’s mean everything
inside is made Positive or >= 0
Example 9 And the opposite
• |5x-12| < -2
• But the stuff inside the ||’s is ALWAYS
positive when you are using real numbers,
this cannot happen!
• Impossible.
Section 3.3 Practice
• Definitions Q 1 to 6
• Solving to get solution sets Q 7 to 36
• Going from graph to inequality with an absolute value
Q 37 to 44
• Is the abs. value the same as the inequality True or False
Q 45 to 52
• Solve and graph the abs. value inequality Q 53 to 72
• Solve each inequality write using interval notation ( )’s
Q 73 to 84