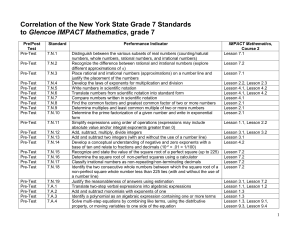
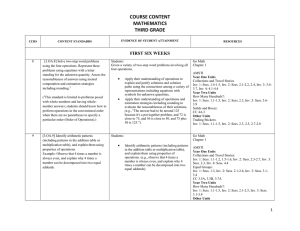
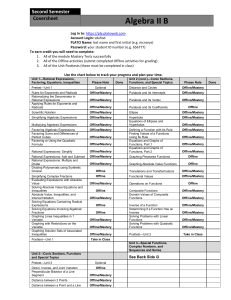
Standard
... Translate numbers from scientific notation into standard form Compare numbers written in scientific notation Find the common factors and greatest common factor of two or more numbers Determine multiples and least common multiple of two or more numbers Determine the prime factorization of a given num ...
... Translate numbers from scientific notation into standard form Compare numbers written in scientific notation Find the common factors and greatest common factor of two or more numbers Determine multiples and least common multiple of two or more numbers Determine the prime factorization of a given num ...
Number Theory & RSA
... Carmichael number: a composite positive integer n which satisfies the equation bn-1 = 1 mod n for all positive integers b which are relatively prime to n Korselt Theorem (1899): A positive odd composite integer n is a Carmichael number if and only if n is square-free, and for all prime divisors p of ...
... Carmichael number: a composite positive integer n which satisfies the equation bn-1 = 1 mod n for all positive integers b which are relatively prime to n Korselt Theorem (1899): A positive odd composite integer n is a Carmichael number if and only if n is square-free, and for all prime divisors p of ...
PPT
... Negative Numbers 32 bits can only represent 232 numbers – if we wish to also represent negative numbers, we can represent 231 positive numbers (incl zero) and 231 negative numbers ...
... Negative Numbers 32 bits can only represent 232 numbers – if we wish to also represent negative numbers, we can represent 231 positive numbers (incl zero) and 231 negative numbers ...
Characterstics of Ternary Semirings
... commutative ternary groups. D. Madhusudhana Rao[8] characterized the primary ideals in ternary semigroups. about T. K. Dutta and S. Kar [4] introduced and studied some properties of ternary semirings which is a generalization of ternary rings. D. Madhusudhana Rao and G. Srinvasa Rao [9, 10] introduc ...
... commutative ternary groups. D. Madhusudhana Rao[8] characterized the primary ideals in ternary semigroups. about T. K. Dutta and S. Kar [4] introduced and studied some properties of ternary semirings which is a generalization of ternary rings. D. Madhusudhana Rao and G. Srinvasa Rao [9, 10] introduc ...
Residue Number Systems
... Simple to Design if mi=2ai or 2ai-1 • Power of 2 Moduli Lead to Simple Design – Standard a-bit Binary Adder – Example: Use 16 Instead of 13 – Exception in Case of Lookup Table Implementation ...
... Simple to Design if mi=2ai or 2ai-1 • Power of 2 Moduli Lead to Simple Design – Standard a-bit Binary Adder – Example: Use 16 Instead of 13 – Exception in Case of Lookup Table Implementation ...
Section2.1notesall
... Solution: 25 11mod 7 since 7 evenly divides 25 – 11 = 14. Because of this, 25 and 11 are in the same congruence class. This is also true since 25 MOD 7 = 11 MOD 7 = 4, that is, they both give the same integer remainder MOD 7. In fact we can say that 32 25 18 11 4 mod 7 , that is, all of th ...
... Solution: 25 11mod 7 since 7 evenly divides 25 – 11 = 14. Because of this, 25 and 11 are in the same congruence class. This is also true since 25 MOD 7 = 11 MOD 7 = 4, that is, they both give the same integer remainder MOD 7. In fact we can say that 32 25 18 11 4 mod 7 , that is, all of th ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.