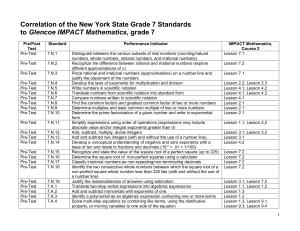
The Fibonacci Numbers
... It looks like the sum of the first few “even” Fibonacci numbers is one less than another Fibonacci number. But which one? F2 + F4 = 1 + 3 = 4 = F5 − 1 F2 + F4 + F6 = 1 + 3 + 8 = 12 = F7 − 1 F2 + F4 + F6 + F8 = 1 + 3 + 8 + 21 = 33 = F9 − 1 F2 + F4 + F6 + F8 + F10 = 1 + 3 + 8 + 21 + 55 = 88 = F11 − 1 ...
... It looks like the sum of the first few “even” Fibonacci numbers is one less than another Fibonacci number. But which one? F2 + F4 = 1 + 3 = 4 = F5 − 1 F2 + F4 + F6 = 1 + 3 + 8 = 12 = F7 − 1 F2 + F4 + F6 + F8 = 1 + 3 + 8 + 21 = 33 = F9 − 1 F2 + F4 + F6 + F8 + F10 = 1 + 3 + 8 + 21 + 55 = 88 = F11 − 1 ...
Representing Numbers Using Fibonacci Variants
... Assume every integer from 1 to n has a Zeckendorf representation. If n + 1 is a Fibonacci number, done. Otherwise, there is some j such that fj < n + 1 < fj+1 . Now n + 1 − fj < n, so has a Zeckendorf representation, and n + 1 − fj < fj+1 − fj = fj−1 , so n + 1 − fj doesn’t contain fj , done. Unique ...
... Assume every integer from 1 to n has a Zeckendorf representation. If n + 1 is a Fibonacci number, done. Otherwise, there is some j such that fj < n + 1 < fj+1 . Now n + 1 − fj < n, so has a Zeckendorf representation, and n + 1 − fj < fj+1 − fj = fj−1 , so n + 1 − fj doesn’t contain fj , done. Unique ...
Floating point numbers in Scilab
... This document is a small introduction to floating point numbers in Scilab. In the first part, we describe the theory of floating point numbers. We present the definition of a floating point system and of a floating point number. Then we present various representation of floating point numbers, inclu ...
... This document is a small introduction to floating point numbers in Scilab. In the first part, we describe the theory of floating point numbers. We present the definition of a floating point system and of a floating point number. Then we present various representation of floating point numbers, inclu ...
Mixed Number & Improper Fraction Notes
... Find the prime factorization of 72. Evaluate: (3 x 2)2 ÷ 4 – 3 ...
... Find the prime factorization of 72. Evaluate: (3 x 2)2 ÷ 4 – 3 ...