The Fibonacci Numbers
... Let’s use this formula: Fn2 = Fn · Fn+1 − Fn · Fn−1 To find out what the sum of the first few SQUARES of Fibonacci numbers is: F12 + F22 + F32 + · · · + Fn2 =???? ...
... Let’s use this formula: Fn2 = Fn · Fn+1 − Fn · Fn−1 To find out what the sum of the first few SQUARES of Fibonacci numbers is: F12 + F22 + F32 + · · · + Fn2 =???? ...
4th ASU 1964 problems
... Collecting the Mathematics tests from the contests choosing the best students is not only my favorite interest but also many different people’s. This selected book is an adequate collection of the Math tests in the Mathematical Olympiads tests from 14 countries, from different regions and from the I ...
... Collecting the Mathematics tests from the contests choosing the best students is not only my favorite interest but also many different people’s. This selected book is an adequate collection of the Math tests in the Mathematical Olympiads tests from 14 countries, from different regions and from the I ...
Grade 7/8 Math Circles Continued Fractions A Fraction of our History
... prices of discounted items. It may be ironic to hear that at one point in history, fractions were not even consider numbers! They were treated as a way to compare whole numbers. In fact, fractions that we use in school today were not used until the 17th century! However, fractions were a crucial fir ...
... prices of discounted items. It may be ironic to hear that at one point in history, fractions were not even consider numbers! They were treated as a way to compare whole numbers. In fact, fractions that we use in school today were not used until the 17th century! However, fractions were a crucial fir ...
“Ciencia Matemática”
... Difficult problems are marked with an asterisk ∗ . Whatever the advertisements inviting people to participate in a Moscow Mathematical Olympiad say, some extra knowledge is essential and taken for granted. The compilers of [Le] and [SCY], not so pressed to save space, earmarked about half the volume ...
... Difficult problems are marked with an asterisk ∗ . Whatever the advertisements inviting people to participate in a Moscow Mathematical Olympiad say, some extra knowledge is essential and taken for granted. The compilers of [Le] and [SCY], not so pressed to save space, earmarked about half the volume ...
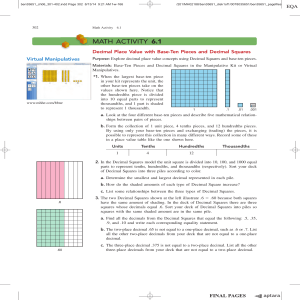
MATH ACTIVITY 6.1
... The person most responsible for our use of decimals is Simon Stevin, a Dutchman. In 1585 Stevin wrote La Disme, the first book on the use of decimals. He not only stated the rules for computing with decimals but also pointed out their practical applications. Stevin showed that business calculations ...
... The person most responsible for our use of decimals is Simon Stevin, a Dutchman. In 1585 Stevin wrote La Disme, the first book on the use of decimals. He not only stated the rules for computing with decimals but also pointed out their practical applications. Stevin showed that business calculations ...
A Transition to Advanced Mathematics
... offer the opportunity for further work in several optional sections: basics of number theory (Section 1.7), combinatorial counting (Section 2.6), order relations and graph theory (Sections 3.4 and 3.5), and image sets and sequences (Sections 4.5 and 4.6). See the diagram on the inside front cover fo ...
... offer the opportunity for further work in several optional sections: basics of number theory (Section 1.7), combinatorial counting (Section 2.6), order relations and graph theory (Sections 3.4 and 3.5), and image sets and sequences (Sections 4.5 and 4.6). See the diagram on the inside front cover fo ...
Infinity

Infinity (symbol: ∞) is an abstract concept describing something without any limit and is relevant in a number of fields, predominantly mathematics and physics.In mathematics, ""infinity"" is often treated as if it were a number (i.e., it counts or measures things: ""an infinite number of terms"") but it is not the same sort of number as natural or real numbers. In number systems incorporating infinitesimals, the reciprocal of an infinitesimal is an infinite number, i.e., a number greater than any real number; see 1/∞.Georg Cantor formalized many ideas related to infinity and infinite sets during the late 19th and early 20th centuries. In the theory he developed, there are infinite sets of different sizes (called cardinalities). For example, the set of integers is countably infinite, while the infinite set of real numbers is uncountable.