Chapter 4 The Group Zoo
... of symmetry groups.” (Hermann Weyl, mathematician) In the previous chapter, we introduced groups (together with subgroups, order of a group, order of an element, abelian and cyclic groups) and saw as examples the group of symmetries of the square and of the rectangle. The concept of group in mathema ...
... of symmetry groups.” (Hermann Weyl, mathematician) In the previous chapter, we introduced groups (together with subgroups, order of a group, order of an element, abelian and cyclic groups) and saw as examples the group of symmetries of the square and of the rectangle. The concept of group in mathema ...
Survey article: Seventy years of Salem numbers
... degree 46.) Further, it was determined by Flammang, Grandcolas and Rhin [43] that the table was complete up to degree 40. This was extended up to degree 44 by Mossinghoff, Rhin and Wu [88] as part of a larger project to find small Mahler measures. Their result shows that if Conjecture 5 is false the ...
... degree 46.) Further, it was determined by Flammang, Grandcolas and Rhin [43] that the table was complete up to degree 40. This was extended up to degree 44 by Mossinghoff, Rhin and Wu [88] as part of a larger project to find small Mahler measures. Their result shows that if Conjecture 5 is false the ...
Mixed Number & Improper Fraction Notes
... that is larger than the denominator. Proper Fraction – a fraction with a numerator that is smaller than the denominator. ...
... that is larger than the denominator. Proper Fraction – a fraction with a numerator that is smaller than the denominator. ...
Book of Proof - people.vcu.edu
... ª set’s elements: If a = 0 0 , b = 10 01 and c = 11 01 , then M = a, b, c . If X is a finite set, its cardinality or size is the number of elements it has, and this number is denoted as | X |. Thus for the sets above, | A | = 4, |B| = 2, |C | = 5, |D | = 4, |E | = 3 and | M | = 3. There is a special ...
... ª set’s elements: If a = 0 0 , b = 10 01 and c = 11 01 , then M = a, b, c . If X is a finite set, its cardinality or size is the number of elements it has, and this number is denoted as | X |. Thus for the sets above, | A | = 4, |B| = 2, |C | = 5, |D | = 4, |E | = 3 and | M | = 3. There is a special ...
Eötvös-Kürschák Competitions
... the memorized knowledge) of the students. The problems have to be solved in a closed room, supervised by impartial observers, within an afternoon. The respect of this competition is created, among others, by the fact that the 10 bests in mathematics and the 10 bests in physics have free admission to ...
... the memorized knowledge) of the students. The problems have to be solved in a closed room, supervised by impartial observers, within an afternoon. The respect of this competition is created, among others, by the fact that the 10 bests in mathematics and the 10 bests in physics have free admission to ...
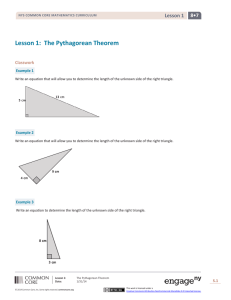
Lesson 1: The Pythagorean Theorem 8•7 Lesson 1
... The number is represented on the number line shown below. Each new line is a magnification of the interval shown above it. For example, the first line is the unit from 0 to 1 divided into 10 equal parts, or tenths. The second line is the interval from 0.8 to 0.9 divided into ten equal parts, or hund ...
... The number is represented on the number line shown below. Each new line is a magnification of the interval shown above it. For example, the first line is the unit from 0 to 1 divided into 10 equal parts, or tenths. The second line is the interval from 0.8 to 0.9 divided into ten equal parts, or hund ...
Book of Proof
... ©ª ©ª empty set is the set that has no elements. We denote it as ;, so ; = . ©ª Whenever you see the symbol ;, it stands for . Observe that |;| = 0. The empty set is the only set whose cardinality is zero. © ª Be very careful how you write the empty set. Don’t write ; when you mean ;. These sets can ...
... ©ª ©ª empty set is the set that has no elements. We denote it as ;, so ; = . ©ª Whenever you see the symbol ;, it stands for . Observe that |;| = 0. The empty set is the only set whose cardinality is zero. © ª Be very careful how you write the empty set. Don’t write ; when you mean ;. These sets can ...
IOSR Journal of Mathematics (IOSR-JM)
... In the context of different proofs, we have a book – the Pythagoras propositions by Prof. Elisha Scott Loomis. There is a collection of 367 proofs Pythagorean Theorem. The author asserts that the number of algebraic proofs is limitless as the number of geometric proofs is. The most popular among all ...
... In the context of different proofs, we have a book – the Pythagoras propositions by Prof. Elisha Scott Loomis. There is a collection of 367 proofs Pythagorean Theorem. The author asserts that the number of algebraic proofs is limitless as the number of geometric proofs is. The most popular among all ...
KENO, KENO BONUS, KENO PATTERN PLAY
... limited to $2,000,000 less the aggregate of all prizes in such draw of $1,000 or less. For draws which include tickets with Keno Doubler, the aggregate amount that may be won in any given draw by all ticket holders whose unadjusted prizes exceeds $1,000 shall be limited to $4,000,000 less the aggreg ...
... limited to $2,000,000 less the aggregate of all prizes in such draw of $1,000 or less. For draws which include tickets with Keno Doubler, the aggregate amount that may be won in any given draw by all ticket holders whose unadjusted prizes exceeds $1,000 shall be limited to $4,000,000 less the aggreg ...
Infinity

Infinity (symbol: ∞) is an abstract concept describing something without any limit and is relevant in a number of fields, predominantly mathematics and physics.In mathematics, ""infinity"" is often treated as if it were a number (i.e., it counts or measures things: ""an infinite number of terms"") but it is not the same sort of number as natural or real numbers. In number systems incorporating infinitesimals, the reciprocal of an infinitesimal is an infinite number, i.e., a number greater than any real number; see 1/∞.Georg Cantor formalized many ideas related to infinity and infinite sets during the late 19th and early 20th centuries. In the theory he developed, there are infinite sets of different sizes (called cardinalities). For example, the set of integers is countably infinite, while the infinite set of real numbers is uncountable.