1 Introduction and Preliminaries
... the Seventeen or Bust project are actually Sierpiński numbers. One can easily check that none of these 8 values is of the form `r where r > 1, and it seems likely to us that the following revision of Conjecture 1 holds. Conjecture 10 . If k is a Sierpiński number that is not of the form `r for som ...
... the Seventeen or Bust project are actually Sierpiński numbers. One can easily check that none of these 8 values is of the form `r where r > 1, and it seems likely to us that the following revision of Conjecture 1 holds. Conjecture 10 . If k is a Sierpiński number that is not of the form `r for som ...
104 Number Theory Problems
... Providing the product of the chosen numbers is equivalent to telling the product of the two unchosen numbers. The only possible products that are achieved by more than one pair of numbers are 12 ({3, 4} and {2, 6}) and 6 ({1, 6} and {2, 3}). But in the second case, the sum of the two (unchosen) numb ...
... Providing the product of the chosen numbers is equivalent to telling the product of the two unchosen numbers. The only possible products that are achieved by more than one pair of numbers are 12 ({3, 4} and {2, 6}) and 6 ({1, 6} and {2, 3}). But in the second case, the sum of the two (unchosen) numb ...
Relevant and Substructural Logics
... I will end with one smaller section Loose Ends, sketching avenues for further work. The major sections, then, are structured thematically, and inside these sections I will endeavour to sketch the core historical lines of development in substructural logics. This, then, will be a conceptual history, ...
... I will end with one smaller section Loose Ends, sketching avenues for further work. The major sections, then, are structured thematically, and inside these sections I will endeavour to sketch the core historical lines of development in substructural logics. This, then, will be a conceptual history, ...
MATH ACTIVITY 6.1
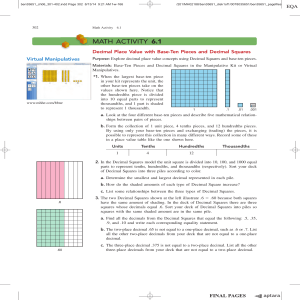
... 3. The two Decimal Squares shown at the left illustrate .6 5 .60 because both squares have the same amount of shading. In the deck of Decimal Squares there are three squares whose decimals equal .6. Sort your deck of Decimal Squares into piles so squares with the same shaded amount are in the same p ...
... 3. The two Decimal Squares shown at the left illustrate .6 5 .60 because both squares have the same amount of shading. In the deck of Decimal Squares there are three squares whose decimals equal .6. Sort your deck of Decimal Squares into piles so squares with the same shaded amount are in the same p ...
Grade 7/8 Math Circles Continued Fractions A Fraction of
... prices of discounted items. It may be ironic to hear that at one point in history, fractions were not even consider numbers! They were treated as a way to compare whole numbers. In fact, fractions that we use in school today were not used until the 17th century! However, fractions were a crucial fir ...
... prices of discounted items. It may be ironic to hear that at one point in history, fractions were not even consider numbers! They were treated as a way to compare whole numbers. In fact, fractions that we use in school today were not used until the 17th century! However, fractions were a crucial fir ...