Sample pages 2 PDF
... 1. One of the oldest mathematical problems concerns perfect numbers. A positive integer N is called perfect, if it equals the sum of its proper divisors, i.e., the equality σ (N) = 2N holds1 . It had been noted already by Euclid that if the numbers 2p − 1 and p are both prime, then 2p−1 (2p − 1) is ...
... 1. One of the oldest mathematical problems concerns perfect numbers. A positive integer N is called perfect, if it equals the sum of its proper divisors, i.e., the equality σ (N) = 2N holds1 . It had been noted already by Euclid that if the numbers 2p − 1 and p are both prime, then 2p−1 (2p − 1) is ...
Ordered and Unordered Factorizations of Integers
... We will also discuss factorizations into distinct parts. In the ordered case, Hd H12L = 5 since we have the factorizations {{2,6}, {3,4}, {4,3}, {6,2}, {12}}. In the unordered case, Pd H12L = 3 since there are three cases, {{4,3}, {6,2}, {12}}. If p is a prime number, then as special cases we have H ...
... We will also discuss factorizations into distinct parts. In the ordered case, Hd H12L = 5 since we have the factorizations {{2,6}, {3,4}, {4,3}, {6,2}, {12}}. In the unordered case, Pd H12L = 3 since there are three cases, {{4,3}, {6,2}, {12}}. If p is a prime number, then as special cases we have H ...
Exam Review Solutions
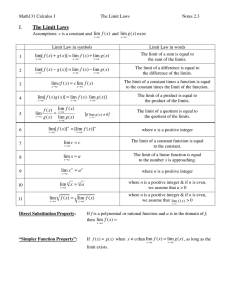
... We must use the first or second derivative test to determine whether this value produces a relative max, min, or neither. The derivative, T ( x) 0 for ...
... We must use the first or second derivative test to determine whether this value produces a relative max, min, or neither. The derivative, T ( x) 0 for ...
mathematics - Target Publications
... the form 6q + r, q is an integer and r = 0, 1, 2, 3, 4, 5 is also of the form 6m+r. Solution: 6q + r is a positive integer, where q is an integer and r = 0, 1, 2, 3, 4, 5 Then, the positive integers are of the form 6q, 6q+1, 6q+2, 6q+3, 6q+4 and 6q+5. Taking cube of each term, we have, (6q)3 = 216 q ...
... the form 6q + r, q is an integer and r = 0, 1, 2, 3, 4, 5 is also of the form 6m+r. Solution: 6q + r is a positive integer, where q is an integer and r = 0, 1, 2, 3, 4, 5 Then, the positive integers are of the form 6q, 6q+1, 6q+2, 6q+3, 6q+4 and 6q+5. Taking cube of each term, we have, (6q)3 = 216 q ...
prob set
... What if we wanted to find the gcd and lcm of a = 12! and b = 1003 . This would be a little more difficult. Listing all the factors would be very bad... I don’t want to even think about writing out the multiples! We need to find another way of doing this. But how? With PRIMES! Prime numbers are the b ...
... What if we wanted to find the gcd and lcm of a = 12! and b = 1003 . This would be a little more difficult. Listing all the factors would be very bad... I don’t want to even think about writing out the multiples! We need to find another way of doing this. But how? With PRIMES! Prime numbers are the b ...
Document
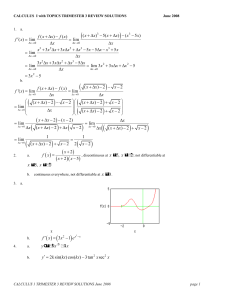
... 7) At how many points do the graphs of y = 3x3 + 1 and y = 3x3 + 6 intersect? _________ 8) For what value of x between π and 3π is 5x y undefined? _________ cos x 1 9) Write the equation of the line with slope 7 that passes through the point (6, -2). _________ ...
... 7) At how many points do the graphs of y = 3x3 + 1 and y = 3x3 + 6 intersect? _________ 8) For what value of x between π and 3π is 5x y undefined? _________ cos x 1 9) Write the equation of the line with slope 7 that passes through the point (6, -2). _________ ...