THE DISTRIBUTION OF PRIME NUMBERS Andrew Granville and K
... It is not easy to find a strategy to prove such a result. Since primes are those integers with no prime factors less than √ or equal to their square-root, one obvious approach to counting the number of primes √ in ( x, x] is to try to estimate the number of integers up to x, with no prime factors ≤ ...
... It is not easy to find a strategy to prove such a result. Since primes are those integers with no prime factors less than √ or equal to their square-root, one obvious approach to counting the number of primes √ in ( x, x] is to try to estimate the number of integers up to x, with no prime factors ≤ ...
The sums of the reciprocals of Fibonacci polynomials and Lucas
... © 2012 Zhengang and Wenpeng; licensee Springer. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original wor ...
... © 2012 Zhengang and Wenpeng; licensee Springer. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original wor ...
Here - UnsolvedProblems.org
... Given this axiom, enough pairs of composites must be formed between the two sequences A-B because the number of free composites of sequence A cannot be greater than the number of primes of sequence B. Conversely, the number of free composites of sequence B cannot be greater than the number of primes ...
... Given this axiom, enough pairs of composites must be formed between the two sequences A-B because the number of free composites of sequence A cannot be greater than the number of primes of sequence B. Conversely, the number of free composites of sequence B cannot be greater than the number of primes ...
SEQUENCES OF PRIMES
... the sequence obtained through the concatenation of the first n positive integers in reverse order). Part Two of this book, “Sequences of primes obtained by the method of concatenation”, brings together 51 articles which aim, using the mentioned method, to highlight sequences of numbers that are rich ...
... the sequence obtained through the concatenation of the first n positive integers in reverse order). Part Two of this book, “Sequences of primes obtained by the method of concatenation”, brings together 51 articles which aim, using the mentioned method, to highlight sequences of numbers that are rich ...
the infinity of the twin primes
... 5 x 3 x 5). It can be the product of a twin primes pair with itself and another prime or primes (e.g., 3 x 5 x 3 x 5 x 23 x 89). It can be the product of a twin primes pair with another twin primes pair or other twin primes pairs (e.g., 11 x 13 x 227 x 229 x 461 x 463) It can be the product of a tw ...
... 5 x 3 x 5). It can be the product of a twin primes pair with itself and another prime or primes (e.g., 3 x 5 x 3 x 5 x 23 x 89). It can be the product of a twin primes pair with another twin primes pair or other twin primes pairs (e.g., 11 x 13 x 227 x 229 x 461 x 463) It can be the product of a tw ...
DIVISIBILITY OF CLASS NUMBERS OF REAL 1. INTRODUCTION
... divisible by 3, Manuscripta Ma th., 111 (2003), no. 2, 262-263. [5] J.H. Evertse and J.H. Silverman : Uniform bounds for the number of solu, Ma th. Proc. Camb. Phil. Soc., 100 (1986), 237-248. tions to [6] Florian Luca: A note on the divisibility of class numbers of real quadratic fields, C. R. Math ...
... divisible by 3, Manuscripta Ma th., 111 (2003), no. 2, 262-263. [5] J.H. Evertse and J.H. Silverman : Uniform bounds for the number of solu, Ma th. Proc. Camb. Phil. Soc., 100 (1986), 237-248. tions to [6] Florian Luca: A note on the divisibility of class numbers of real quadratic fields, C. R. Math ...
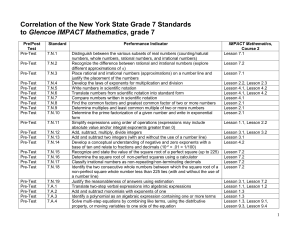
Standard
... Recognize and state the value of the square root of a perfect square (up to 225) Determine the square root of non-perfect squares using a calculator Classify irrational numbers as non-repeating/non-terminating decimals Identify the two consecutive whole numbers between which the square root of a non ...
... Recognize and state the value of the square root of a perfect square (up to 225) Determine the square root of non-perfect squares using a calculator Classify irrational numbers as non-repeating/non-terminating decimals Identify the two consecutive whole numbers between which the square root of a non ...
NORMALITY OF NUMBERS GENERATED BY THE VALUES OF
... is normal in base 10. These examples correspond to the choice f (x) = x in (1.1). Davenport and Erdös [5] considered the case where f (x) is a polynomial whose values at x = 1, 2, . . . are always integers and showed that in this case the numbers θq (f ) and τq (f ) are normal. For f (x) a polynomi ...
... is normal in base 10. These examples correspond to the choice f (x) = x in (1.1). Davenport and Erdös [5] considered the case where f (x) is a polynomial whose values at x = 1, 2, . . . are always integers and showed that in this case the numbers θq (f ) and τq (f ) are normal. For f (x) a polynomi ...
Advanced Problems and Solutions
... Right and left-normal sequences, 5.5(1967)436 Partial Solution, 11.1(1973)77; Another Piece, 11.2(1973)186; Ghost from the Past [Comment], 27.1(1989)95 Sums of series with three Fibonacci coefficients, 6.1(1968)50 Multi-Variable Series, 7.3(1969)278 Recurrence relations for a product of Fibonacci po ...
... Right and left-normal sequences, 5.5(1967)436 Partial Solution, 11.1(1973)77; Another Piece, 11.2(1973)186; Ghost from the Past [Comment], 27.1(1989)95 Sums of series with three Fibonacci coefficients, 6.1(1968)50 Multi-Variable Series, 7.3(1969)278 Recurrence relations for a product of Fibonacci po ...
Grade 7/8 Math Circles Continued Fractions A Fraction of our History
... prices of discounted items. It may be ironic to hear that at one point in history, fractions were not even consider numbers! They were treated as a way to compare whole numbers. In fact, fractions that we use in school today were not used until the 17th century! However, fractions were a crucial fir ...
... prices of discounted items. It may be ironic to hear that at one point in history, fractions were not even consider numbers! They were treated as a way to compare whole numbers. In fact, fractions that we use in school today were not used until the 17th century! However, fractions were a crucial fir ...