List of available projects - HTTrack Website Copier
... Step. 16 : Divide 8 by 2 i.e.,, 0.0526315789473684 ( 4 times, No remainder ) Step. 17 : Divide 4 by 2 i.e.,, 0.05263157894736842 ( 2 times, No remainder ) Step. 18 : Divide 2 by 2 i.e.,, 0.052631578947368421 ( 1 time, No remainder ) Now from step 19, i.e.,, dividing 1 by 2, Step 2 to Step. 18 repeat ...
... Step. 16 : Divide 8 by 2 i.e.,, 0.0526315789473684 ( 4 times, No remainder ) Step. 17 : Divide 4 by 2 i.e.,, 0.05263157894736842 ( 2 times, No remainder ) Step. 18 : Divide 2 by 2 i.e.,, 0.052631578947368421 ( 1 time, No remainder ) Now from step 19, i.e.,, dividing 1 by 2, Step 2 to Step. 18 repeat ...
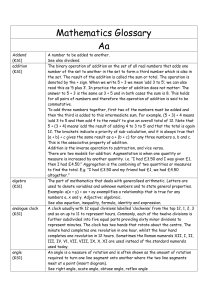
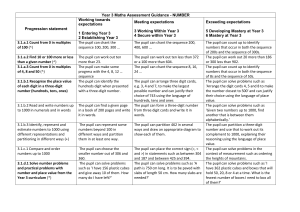
Year 3 Maths Assessment Guidance
... The pupil can readily recall the facts from the 2, 3, 4, 5, 8 and 10 multiplication tables and use them within a calculation, such as 'There are eight apples in a bag. How many are in four such bags?' and solve word problems such as 'There are 96 cupcakes to put into boxes which hold 8 cupcakes each ...
... The pupil can readily recall the facts from the 2, 3, 4, 5, 8 and 10 multiplication tables and use them within a calculation, such as 'There are eight apples in a bag. How many are in four such bags?' and solve word problems such as 'There are 96 cupcakes to put into boxes which hold 8 cupcakes each ...
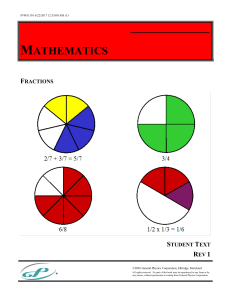
Number Patterns and Fractions
... factored so the factor pairs are written underneath the 6. Each number is continued to be factored until the factors are all prime numbers. Note that 36 is written as a product of its primes at the bottom of the factor tree. Write the 2s together and the 3s together. Grouping like factors will help ...
... factored so the factor pairs are written underneath the 6. Each number is continued to be factored until the factors are all prime numbers. Note that 36 is written as a product of its primes at the bottom of the factor tree. Write the 2s together and the 3s together. Grouping like factors will help ...
Intermediate Math Circles November 25, 2009 Diophantine
... The next two are harder, but if you can, find a rule for. . . (6) When a number is divisible by 8. (7) When a number is divisible by 7. (Hint: the rule has something to do with breaking the number down into the ones digit, and then the number made up of all the other digits: 1031 = 103 and 1: Now, c ...
... The next two are harder, but if you can, find a rule for. . . (6) When a number is divisible by 8. (7) When a number is divisible by 7. (Hint: the rule has something to do with breaking the number down into the ones digit, and then the number made up of all the other digits: 1031 = 103 and 1: Now, c ...
Review Problem 1
... cout >> “Enter another number: ;” cin >> number 2, number1 + number2 = sum; cout << ‘The sum of the two numbers is ” << sum; ...
... cout >> “Enter another number: ;” cin >> number 2, number1 + number2 = sum; cout << ‘The sum of the two numbers is ” << sum; ...
Experimental Error 3
... You should write one of the three numbers above, instead of 92 500, to indicate how many figures are actually known. Zeros are significant when they occur (1) in the middle of a number or (2) at the end of a number on the right-hand side of a decimal point. The last significant digit (farthest to th ...
... You should write one of the three numbers above, instead of 92 500, to indicate how many figures are actually known. Zeros are significant when they occur (1) in the middle of a number or (2) at the end of a number on the right-hand side of a decimal point. The last significant digit (farthest to th ...
3810-08
... Consider the sum of 1 and -2 …. we get -1 Consider the sum of 2 and -1 …. we get +1 This format can directly undergo addition without any conversions! Each number represents the quantity x31 -231 + x30 230 + x29 229 + … + x1 21 + x0 20 ...
... Consider the sum of 1 and -2 …. we get -1 Consider the sum of 2 and -1 …. we get +1 This format can directly undergo addition without any conversions! Each number represents the quantity x31 -231 + x30 230 + x29 229 + … + x1 21 + x0 20 ...
Unit 3 Expressions and Equations: Equivalent
... In the exercises below, students can signal their answers by pointing to the correct word. Exercises: What property is the equation an example of, commutative (A) or associative (B)? a) 3 × 7 = 7 × 3 b) (3 + 4) + 5 = 3 + (4 + 5) c) 2 + 43 = 43 + 2 d) 2 × (5 × 11) = (2 × 5) × 11 Answers: a) A, b) B, ...
... In the exercises below, students can signal their answers by pointing to the correct word. Exercises: What property is the equation an example of, commutative (A) or associative (B)? a) 3 × 7 = 7 × 3 b) (3 + 4) + 5 = 3 + (4 + 5) c) 2 + 43 = 43 + 2 d) 2 × (5 × 11) = (2 × 5) × 11 Answers: a) A, b) B, ...
Lesson 7: Six different symbols for fractions
... “Your days are numbered” really means: There is a whole number that is the same as (or is greater than) the number of days you will remain alive. When used as a verb, the word “number” can mean either to count or simply to find a name for the size of a collection. For example, the statement in (Gene ...
... “Your days are numbered” really means: There is a whole number that is the same as (or is greater than) the number of days you will remain alive. When used as a verb, the word “number” can mean either to count or simply to find a name for the size of a collection. For example, the statement in (Gene ...
Elementary arithmetic
Elementary arithmetic is the simplified portion of arithmetic that includes the operations of addition, subtraction, multiplication, and division. It should not be confused with elementary function arithmetic.Elementary arithmetic starts with the natural numbers and the written symbols (digits) that represent them. The process for combining a pair of these numbers with the four basic operations traditionally relies on memorized results for small values of numbers, including the contents of a multiplication table to assist with multiplication and division.Elementary arithmetic also includes fractions and negative numbers, which can be represented on a number line.