* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Rational and Irrational Numbers
Foundations of mathematics wikipedia , lookup
Positional notation wikipedia , lookup
Law of large numbers wikipedia , lookup
Location arithmetic wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Infinitesimal wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Non-standard analysis wikipedia , lookup
Proofs of Fermat's little theorem wikipedia , lookup
Surreal number wikipedia , lookup
Large numbers wikipedia , lookup
Hyperreal number wikipedia , lookup
Division by zero wikipedia , lookup
P-adic number wikipedia , lookup
Real number wikipedia , lookup
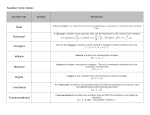
The Set of Real Numbers Honors Math – Grade 8 KEY CONCEPT The Real Numbers The Real Numbers consist of all rational and irrational numbers. The Venn Diagram below shows the relationships among the sets of numbers. Real Numbers Rational Numbers Integers Whole Numbers Natural Numbers Irrational Numbers Classify the following real numbers. To decide to which set of numbers a real number belongs, you may need to rename the number in a different form. 0.54 This is a repeating decimal. Rational number 44 4 11 Whole number Integer Rational number This is a natural number. KEY CONCEPT The Completeness Property for Points on the Number Line Every real number corresponds to exactly one point on a number line and every point on the number line corresponds to exactly one real number. The origin of a number line is zero. Positive and negative numbers are often called signed numbers. Points to the left of zero correspond to negative numbers. Points to the right of zero correspond to positive numbers. Zero is neither positive nor negative. A number line can help compare and order real numbers. Graph the following real numbers. 4 2 , 3 , , 2, and 1.7 5 The farther to the right a number is on the number line, the greater it is. Order the real numbers from least to greatest. 4 3 , 1.7, 2 , 2, 5 The absolute value of a real number, n, is the distance from 0 to n on a number line. n Since distance is always positive, the absolute value of a nonzero number is always positive. 3.5 3.5 3.5 3.5 Two real numbers are opposites (or additive inverses) if they are on opposite sides of 0 and they have the same absolute value. KEY CONCEPT For any real number a, a + (–a) = 0 (5.6) 5.6 Read “the opposite of 5.6.” Additive Inverse Property and –a + a = 0 (5.6) 5.6 Read “the opposite of -5.6.” Find the value of each expression. (30) (12) What is the opposite of -30? What is the opposite of -12? First find the opposite of each factor. Then evaluate the expression. 30 12 360 Find the value of each expression. 6.9 2.9 What is the absolute value of 6.9? What is the absolute value of 2.9? First find the absolute value of each number. Then evaluate the expression. 6.9 2.9 4 Find the value of each expression. 9 75 675 (675) 675 Find the opposite of the absolute value of the product of 9 and 75. First multiply. Find the opposite. Find the absolute value. Find the opposite of the absolute value of the sum of 3.9 and 5.2. First add. 3.9 5.2 9.1 (9.1) 9.1 When you apply an operation (for example addition) to any numbers in a set and the result is also a number in that set, the set is said to be closed under the operation. This is called the Closure Property. Determine if each set of numbers is closed under the indicated operation. The set of real numbers under addition. 2 1 3 8 8 8 4 3 7 This means to check whether the sum of any two real numbers will result in another real number. The set of real numbers is closed under addition. The set of integers under division. 82 4 2 8 0.25 A counterexample shows that a set of numbers is not closed under an operation. This means to check whether the quotient of any two integers will result in another integer. The set of integers is not closed under division.