Elementary Problems and Solutions
... Edited by A.P. Hillman To:Even subscripted Fibonacci and Lucas reciprocals, 5.1(1967)108 So: Another Series Equality, 5.5(1967)470 To:Generalized Fibonacci-Lucas identity, 5.2(1967)201 So: Generalization of Fn Ln = F2n-1 + F2n-2, 6.1(1968)90 To:Fractional parts of powers of the golden number, 5.2(19 ...
... Edited by A.P. Hillman To:Even subscripted Fibonacci and Lucas reciprocals, 5.1(1967)108 So: Another Series Equality, 5.5(1967)470 To:Generalized Fibonacci-Lucas identity, 5.2(1967)201 So: Generalization of Fn Ln = F2n-1 + F2n-2, 6.1(1968)90 To:Fractional parts of powers of the golden number, 5.2(19 ...
Standard
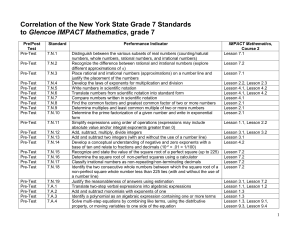
... Distinguish between the various subsets of real numbers (counting/natural numbers, whole numbers, rational numbers, and irrational numbers) Recognize the difference between rational and irrational numbers (explore different approximations of ) Place rational and irrational numbers (approximations) ...
... Distinguish between the various subsets of real numbers (counting/natural numbers, whole numbers, rational numbers, and irrational numbers) Recognize the difference between rational and irrational numbers (explore different approximations of ) Place rational and irrational numbers (approximations) ...
Characterstics of Ternary Semirings
... multiplication of complex numbers being the two ternary semiring compositions. NOTE II.14 : The set M of all n × n matrices with their elements as real numbers (rational numbers, complex numbers, integers) is a non-commutative ternary semiring, with respect to addition and ternary multiplication of ...
... multiplication of complex numbers being the two ternary semiring compositions. NOTE II.14 : The set M of all n × n matrices with their elements as real numbers (rational numbers, complex numbers, integers) is a non-commutative ternary semiring, with respect to addition and ternary multiplication of ...
Section2.2notesall
... 2. Frequency analysis. Quicker way which involves matching to highly frequently occurring ciphertext letters with two highly frequently occurring plaintext letters. Involves solving a system of equations MOD 26. The next example illustrates method 2. Example 16: Suppose we receive a ciphertext that ...
... 2. Frequency analysis. Quicker way which involves matching to highly frequently occurring ciphertext letters with two highly frequently occurring plaintext letters. Involves solving a system of equations MOD 26. The next example illustrates method 2. Example 16: Suppose we receive a ciphertext that ...
Characterization of Transition Edge Sensors for the Millimeter Bolometer Array Camera on the Atacama Cosmology Telescope
... The Thevenin voltage and the equivalent impedance constructed from the transfer function measurements. The figure on the left shows both the real part (blue), the imaginary part (red), and the amplitude (dashed blue) of the Thevenin voltage, up to the factor C(f )/Vbias (f ) described in the text. T ...
... The Thevenin voltage and the equivalent impedance constructed from the transfer function measurements. The figure on the left shows both the real part (blue), the imaginary part (red), and the amplitude (dashed blue) of the Thevenin voltage, up to the factor C(f )/Vbias (f ) described in the text. T ...
MATHEMATICS
... Elem./MS: D.RE.e4.SI.EG01a, D.RE.m7.SI.EG01a HS: EHSCE.SI.L1.2.4a Elem: Gather and/or organize data using pictures or concrete objects that can be collected and sorted (maximum of 10 objects and 1 attribute). MS/HS: Gather and/or organize data using pictures or concrete objects to represent real lif ...
... Elem./MS: D.RE.e4.SI.EG01a, D.RE.m7.SI.EG01a HS: EHSCE.SI.L1.2.4a Elem: Gather and/or organize data using pictures or concrete objects that can be collected and sorted (maximum of 10 objects and 1 attribute). MS/HS: Gather and/or organize data using pictures or concrete objects to represent real lif ...
Mathematics of radio engineering

The mathematics of radio engineering is the mathematical description by complex analysis of the electromagnetic theory applied to radio. Waves have been studied since ancient times and many different techniques have developed of which the most useful idea is the superposition principle which apply to radio waves. The Huygen's principle, which says that each wavefront creates an infinite number of new wavefronts that can be added, is the base for this analysis.