Die Grundlagen der Arithmetik §§82–83
... Frege observes that it has not yet been stated that every number immediately follows or is followed by another. He then states: 6. Every number except 0 immediately follows a number in the natural sequence of numbers. It is clear from §44 of Grundgesetze6 that Frege did not take (6) to imply that 0 ...
... Frege observes that it has not yet been stated that every number immediately follows or is followed by another. He then states: 6. Every number except 0 immediately follows a number in the natural sequence of numbers. It is clear from §44 of Grundgesetze6 that Frege did not take (6) to imply that 0 ...
Section 3.3 Equivalence Relation
... Classifying objects and placing similar objects into groups provides a way to organize information and focus attention on the similarities of like objects and not on the dissimilarities of dislike objects. Mathematicians have been classifying objects for millennia. Lines in the plane can be subdivid ...
... Classifying objects and placing similar objects into groups provides a way to organize information and focus attention on the similarities of like objects and not on the dissimilarities of dislike objects. Mathematicians have been classifying objects for millennia. Lines in the plane can be subdivid ...
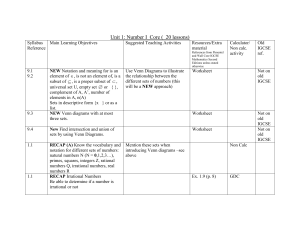
Unit 3 Introduction to Rational Number Class - VII - CBSE
... making the educational content and methodology more sensitive and responsive to the global needs. It signifies the emergence of a fresh thought process in imparting a curriculum which would restore the independence of the learner to pursue the learning process in harmony with the existing personal, ...
... making the educational content and methodology more sensitive and responsive to the global needs. It signifies the emergence of a fresh thought process in imparting a curriculum which would restore the independence of the learner to pursue the learning process in harmony with the existing personal, ...
Principle of Mathematical Induction
... used to prove that a proposition is true for all natural numbers 1,2,3,… , although there are many variations of the basic method. The method is particularly important in discrete mathematics, and one often sees theorems proven by induction in areas like computer science. The technique is so intuiti ...
... used to prove that a proposition is true for all natural numbers 1,2,3,… , although there are many variations of the basic method. The method is particularly important in discrete mathematics, and one often sees theorems proven by induction in areas like computer science. The technique is so intuiti ...
Document
... • Let A be a set with k + 1 elements, and let a be any element of A (there is one, since k + 1 ≥ 1) • Then A - {a} has k elements, and 2A-{a} has 2k elements by the induction hypothesis; therefore, A has 2k subsets that do not contain a and 2k subsets that do contain a, for a total of 2k+1 subsets ...
... • Let A be a set with k + 1 elements, and let a be any element of A (there is one, since k + 1 ≥ 1) • Then A - {a} has k elements, and 2A-{a} has 2k elements by the induction hypothesis; therefore, A has 2k subsets that do not contain a and 2k subsets that do contain a, for a total of 2k+1 subsets ...
Rational Numbers
... At the beginning of June, the Frosty Snow Blower Company was $235.46 in debt. By the end of August, the company had increased its debt by $156.71. a) Use a rational number to represent each amount. b) Calculate how much the company owed at the end of August. 씰A Solution A debt of $235.46 can be repr ...
... At the beginning of June, the Frosty Snow Blower Company was $235.46 in debt. By the end of August, the company had increased its debt by $156.71. a) Use a rational number to represent each amount. b) Calculate how much the company owed at the end of August. 씰A Solution A debt of $235.46 can be repr ...
Peano`s Arithmetic
... on the natural numbers; sometimes they even refer to them as Dedekind-Peano axioms. This is because in the year prior to the publication of Arithmetices principia, Dedekind published Was sind und was sollen die Zahlen, a book which contained very similar results. Peano was completely unaware of its ...
... on the natural numbers; sometimes they even refer to them as Dedekind-Peano axioms. This is because in the year prior to the publication of Arithmetices principia, Dedekind published Was sind und was sollen die Zahlen, a book which contained very similar results. Peano was completely unaware of its ...
Surreal number
In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number. The surreals share many properties with the reals, including a total order ≤ and the usual arithmetic operations (addition, subtraction, multiplication, and division); as such, they form an ordered field. (Strictly speaking, the surreals are not a set, but a proper class.) If formulated in Von Neumann–Bernays–Gödel set theory, the surreal numbers are the largest possible ordered field; all other ordered fields, such as the rationals, the reals, the rational functions, the Levi-Civita field, the superreal numbers, and the hyperreal numbers, can be realized as subfields of the surreals. It has also been shown (in Von Neumann–Bernays–Gödel set theory) that the maximal class hyperreal field is isomorphic to the maximal class surreal field; in theories without the axiom of global choice, this need not be the case, and in such theories it is not necessarily true that the surreals are the largest ordered field. The surreals also contain all transfinite ordinal numbers; the arithmetic on them is given by the natural operations.In 1907 Hahn introduced Hahn series as a generalization of formal power series, and Hausdorff introduced certain ordered sets called ηα-sets for ordinals α and asked if it was possible to find a compatible ordered group or field structure. In 1962 Alling used a modified form of Hahn series to construct such ordered fields associated to certain ordinals α, and taking α to be the class of all ordinals in his construction gives a class that is an ordered field isomorphic to the surreal numbers.Research on the go endgame by John Horton Conway led to a simpler definition and construction of the surreal numbers. Conway's construction was introduced in Donald Knuth's 1974 book Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness. In his book, which takes the form of a dialogue, Knuth coined the term surreal numbers for what Conway had called simply numbers. Conway later adopted Knuth's term, and used surreals for analyzing games in his 1976 book On Numbers and Games.