Theory of Logic Circuits Laboratory manual Exercise 6
... then we should use at least 9 positions for integer and 5 positions for fraction, so (A)2=(011010011.01101)2 1. Using sign-magnitude representation: (-A)2=(111010011.01101)2 2. Using 1's complement representation: (-A)2=(100101100.10010)2 3. Using 2s complement representation: (-A)2=(100101100.10011 ...
... then we should use at least 9 positions for integer and 5 positions for fraction, so (A)2=(011010011.01101)2 1. Using sign-magnitude representation: (-A)2=(111010011.01101)2 2. Using 1's complement representation: (-A)2=(100101100.10010)2 3. Using 2s complement representation: (-A)2=(100101100.10011 ...
Elementary number theory in nine chapters
... polyhedra, introduced the term polygonal number to denote those natural numbers that were oblong, triangular, square, and so forth. Earlier, the fourth century BC philosopher Plato, continuing the Pythagorean tradition, founded a school of philosophy near Athens in an area that had been dedicated to ...
... polyhedra, introduced the term polygonal number to denote those natural numbers that were oblong, triangular, square, and so forth. Earlier, the fourth century BC philosopher Plato, continuing the Pythagorean tradition, founded a school of philosophy near Athens in an area that had been dedicated to ...
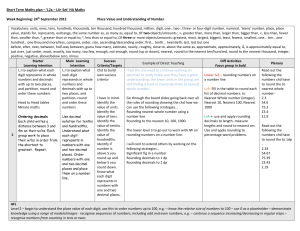
Maths Calculation Policy 2016
... Addition and subtraction: Children are taught to use place value and number facts to add and subtract numbers mentally and they will develop a range of strategies to enable them to discard the ‘counting in 1s’ or fingers-based methods of Key Stage 1. In particular, children will learn to add and sub ...
... Addition and subtraction: Children are taught to use place value and number facts to add and subtract numbers mentally and they will develop a range of strategies to enable them to discard the ‘counting in 1s’ or fingers-based methods of Key Stage 1. In particular, children will learn to add and sub ...
On the expression of a number in the form ax2 + by + cz + du
... In neither of these cases is N − du2 of the form 4λ (8µ + 7), and therefore in either case it can be expressed in the form x2 + y 2 + z 2 . Finally, let d = 7. If µ is equal to 0,1, or 2, take u = 2λ . Then N − du2 is equal to 0, 2 · 4λ+1 , or 4λ+2 . If µ ≥ 3, take u = 2λ+1 . Then N − du2 = 4λ (8µ − ...
... In neither of these cases is N − du2 of the form 4λ (8µ + 7), and therefore in either case it can be expressed in the form x2 + y 2 + z 2 . Finally, let d = 7. If µ is equal to 0,1, or 2, take u = 2λ . Then N − du2 is equal to 0, 2 · 4λ+1 , or 4λ+2 . If µ ≥ 3, take u = 2λ+1 . Then N − du2 = 4λ (8µ − ...
Sample - University of Utah Math Department
... 9. Determine which amounts of postage can be formed using just 4 cent and 7 cent stamps. We solved the Diophantine Equation before, and checked whether any solutions are pairs of nonnegative integers. This time we use strong induction. The first step is to try some sums and guess which values are po ...
... 9. Determine which amounts of postage can be formed using just 4 cent and 7 cent stamps. We solved the Diophantine Equation before, and checked whether any solutions are pairs of nonnegative integers. This time we use strong induction. The first step is to try some sums and guess which values are po ...
Solution Set 1 - MIT Mathematics
... since each open interval (a, b) in S is contained in Sn,m when n > 1/(b − a) and m ≥ max(|a|, |b|). Thus, S is a countable union of finite sets and hence countable. 4. There is an uncountable set of nested subsets of N. Because Q is in one-to-one correspondence with N, it suffices to find subsets of ...
... since each open interval (a, b) in S is contained in Sn,m when n > 1/(b − a) and m ≥ max(|a|, |b|). Thus, S is a countable union of finite sets and hence countable. 4. There is an uncountable set of nested subsets of N. Because Q is in one-to-one correspondence with N, it suffices to find subsets of ...
Chapter 1
... intervals I n are bounded but not closed. (b) The nested intervals I n x R:n x have no point that is common to all of them since this number, x, would then have to satisfy x n for all n. This would contradict theorem 1.4.The nested interval theorem is not violated by this example since the intervals ...
... intervals I n are bounded but not closed. (b) The nested intervals I n x R:n x have no point that is common to all of them since this number, x, would then have to satisfy x n for all n. This would contradict theorem 1.4.The nested interval theorem is not violated by this example since the intervals ...
Session 1 What Is a Number System?
... Tip C3(a). You may notice that by taking two numbers on the number line—1 and 3, for example—and dividing the smaller by the larger, it will be necessary to add fractions between the integers already on the number line. Tip C3(b). The multiplicative inverse of a number is the number by which you mus ...
... Tip C3(a). You may notice that by taking two numbers on the number line—1 and 3, for example—and dividing the smaller by the larger, it will be necessary to add fractions between the integers already on the number line. Tip C3(b). The multiplicative inverse of a number is the number by which you mus ...
Surreal number
In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number. The surreals share many properties with the reals, including a total order ≤ and the usual arithmetic operations (addition, subtraction, multiplication, and division); as such, they form an ordered field. (Strictly speaking, the surreals are not a set, but a proper class.) If formulated in Von Neumann–Bernays–Gödel set theory, the surreal numbers are the largest possible ordered field; all other ordered fields, such as the rationals, the reals, the rational functions, the Levi-Civita field, the superreal numbers, and the hyperreal numbers, can be realized as subfields of the surreals. It has also been shown (in Von Neumann–Bernays–Gödel set theory) that the maximal class hyperreal field is isomorphic to the maximal class surreal field; in theories without the axiom of global choice, this need not be the case, and in such theories it is not necessarily true that the surreals are the largest ordered field. The surreals also contain all transfinite ordinal numbers; the arithmetic on them is given by the natural operations.In 1907 Hahn introduced Hahn series as a generalization of formal power series, and Hausdorff introduced certain ordered sets called ηα-sets for ordinals α and asked if it was possible to find a compatible ordered group or field structure. In 1962 Alling used a modified form of Hahn series to construct such ordered fields associated to certain ordinals α, and taking α to be the class of all ordinals in his construction gives a class that is an ordered field isomorphic to the surreal numbers.Research on the go endgame by John Horton Conway led to a simpler definition and construction of the surreal numbers. Conway's construction was introduced in Donald Knuth's 1974 book Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness. In his book, which takes the form of a dialogue, Knuth coined the term surreal numbers for what Conway had called simply numbers. Conway later adopted Knuth's term, and used surreals for analyzing games in his 1976 book On Numbers and Games.