Rational Numbers
... A composite number is a natural number which has more than two factors. For example, 26 is a composite number since it has more than two factors: 1, 2, 13 and 26. Notice that these definitions indicate that one (1) is neither prime nor composite. Every composite number can be factorised as a product ...
... A composite number is a natural number which has more than two factors. For example, 26 is a composite number since it has more than two factors: 1, 2, 13 and 26. Notice that these definitions indicate that one (1) is neither prime nor composite. Every composite number can be factorised as a product ...
15_cardinality
... A to set B, but not from B to A, we say |A| < |B| Cantor–Schröder–Bernstein theorem: If |A| ≤ |B| and |B| ≤ |A|, then |A| = |B| ...
... A to set B, but not from B to A, we say |A| < |B| Cantor–Schröder–Bernstein theorem: If |A| ≤ |B| and |B| ≤ |A|, then |A| = |B| ...
Transfinite Chomp
... Each component box has each side length ωe, for non-negative integer e Discard any box contained within another to form S’ If Y is reachable from X, size(Y) < size(X) Chomp terminates after finitely many moves ...
... Each component box has each side length ωe, for non-negative integer e Discard any box contained within another to form S’ If Y is reachable from X, size(Y) < size(X) Chomp terminates after finitely many moves ...
Applications of imaginary numbers
... number was viewed as being a pretend number invented for convenience sake. (But then, when you think about it, aren't all numbers inventions? It's not like numbers grow on trees! They live in our heads. We made them all up! Why not invent a new one, as long as it works okay with what we already have ...
... number was viewed as being a pretend number invented for convenience sake. (But then, when you think about it, aren't all numbers inventions? It's not like numbers grow on trees! They live in our heads. We made them all up! Why not invent a new one, as long as it works okay with what we already have ...
THE INTEGERS
... The multiplication rule is a little trickier. To see what the correct definition should be, we recall that (a, b) and (c, d) can be thought of as a – b and c – d, so expanding the product (a – b)(c – d), we obtain ac + bd – ad – bc = ac + bd – (ad + bc). Hence we define multiplication of the ordered ...
... The multiplication rule is a little trickier. To see what the correct definition should be, we recall that (a, b) and (c, d) can be thought of as a – b and c – d, so expanding the product (a – b)(c – d), we obtain ac + bd – ad – bc = ac + bd – (ad + bc). Hence we define multiplication of the ordered ...
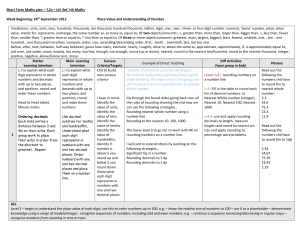
Enfield LA Mental Calculation Guidance
... their fluency. e.g. 90 ÷ 13 = 6 12⁄13 90 ÷ 13 = 6.92 (rounded to two decimal places). Understand that multiplication and division are inverse operations, and use this to check result, Recall and use equivalences between simple fractions, e.g. 6783 ÷ 19 = 357 appears to be about right because 350 x 2 ...
... their fluency. e.g. 90 ÷ 13 = 6 12⁄13 90 ÷ 13 = 6.92 (rounded to two decimal places). Understand that multiplication and division are inverse operations, and use this to check result, Recall and use equivalences between simple fractions, e.g. 6783 ÷ 19 = 357 appears to be about right because 350 x 2 ...
Comparing Infinite Sets - University of Arizona Math
... keep going forever on the number of elements in the finite set. In an infinite set, you still have the first element, second element, and so on. However there is no last element because the infinite set will contain a kth element and there will always be a (k+1)th element because there is no limit t ...
... keep going forever on the number of elements in the finite set. In an infinite set, you still have the first element, second element, and so on. However there is no last element because the infinite set will contain a kth element and there will always be a (k+1)th element because there is no limit t ...
example
... Example 4 Stock Price Change. Tell which integers correspond to this situation: Hal owns another stock whose price increases $2 per share over the same period. The integer 2 corresponds to the increase in the stock value. ...
... Example 4 Stock Price Change. Tell which integers correspond to this situation: Hal owns another stock whose price increases $2 per share over the same period. The integer 2 corresponds to the increase in the stock value. ...
Chapter 4, Mathematics
... Just defining addition and multiplication like this is not sufficient to establish integer arithmetic. We need to show also that the definitions are consistent and correspond to the operations of addition and multiplication for integers. We have defined integers as equivalence classes of pairs of na ...
... Just defining addition and multiplication like this is not sufficient to establish integer arithmetic. We need to show also that the definitions are consistent and correspond to the operations of addition and multiplication for integers. We have defined integers as equivalence classes of pairs of na ...
Surreal number
In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number. The surreals share many properties with the reals, including a total order ≤ and the usual arithmetic operations (addition, subtraction, multiplication, and division); as such, they form an ordered field. (Strictly speaking, the surreals are not a set, but a proper class.) If formulated in Von Neumann–Bernays–Gödel set theory, the surreal numbers are the largest possible ordered field; all other ordered fields, such as the rationals, the reals, the rational functions, the Levi-Civita field, the superreal numbers, and the hyperreal numbers, can be realized as subfields of the surreals. It has also been shown (in Von Neumann–Bernays–Gödel set theory) that the maximal class hyperreal field is isomorphic to the maximal class surreal field; in theories without the axiom of global choice, this need not be the case, and in such theories it is not necessarily true that the surreals are the largest ordered field. The surreals also contain all transfinite ordinal numbers; the arithmetic on them is given by the natural operations.In 1907 Hahn introduced Hahn series as a generalization of formal power series, and Hausdorff introduced certain ordered sets called ηα-sets for ordinals α and asked if it was possible to find a compatible ordered group or field structure. In 1962 Alling used a modified form of Hahn series to construct such ordered fields associated to certain ordinals α, and taking α to be the class of all ordinals in his construction gives a class that is an ordered field isomorphic to the surreal numbers.Research on the go endgame by John Horton Conway led to a simpler definition and construction of the surreal numbers. Conway's construction was introduced in Donald Knuth's 1974 book Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness. In his book, which takes the form of a dialogue, Knuth coined the term surreal numbers for what Conway had called simply numbers. Conway later adopted Knuth's term, and used surreals for analyzing games in his 1976 book On Numbers and Games.