Download The Real Number System

Warm UP
Round to the indicated place value.
1. 782 to the nearest tens
2. 3, 251 to the nearest hundred
3. 28, 341 round to the nearest ten
thousand
4. 719, 219 round to the largest place
5. 732 to the nearest tens
6. 36 to the largest place
Lesson 1.1
Real Number Sets
S1.C1.PO1
SWBAT: Recognize, provide examples
of and create a hierarchy for all of
the real number sets.
Natural Numbers
(Counting Numbers)
•start at 1, 2, 3,…
Whole Numbers
•start at 0, 1, 2, 3 …
Integers
•Positive and negative
whole numbers.
… -3, -2, -1, 0, 1, 2, 3, …
Rational Numbers
• Any number that can be
written as a fraction.
This includes all
terminating and
repeating decimals.
( 1 ½ , 8.19, 5, -2, 8. 3)
Irrational Numbers
•Any decimal that
does not repeat or
terminate.
 , 7, 5, 217
Real Numbers
•All rational and
irrational numbers.
Lesson 1.1B
Finite, Infinite, & Empty Sets
• OBJ: SWBAT determine the difference
between finite and infinite sets.
• Standard: S1C1PO2
What is a set?
A set is a group of objects.
Usually in a math class we will deal
with sets of NUMBERS!
A set could be “the number of
people in the room wearing white
shoes.” Or, “all objects in the
room that are black.”
But wait!
Just how many types of sets are
there?
There are three different types of sets:
1. First type is: A finite set.
2. Second type is: An infinite set.
3. Third type is: An empty set
Finite Sets
Finite sets have an exact number of
elements in the set.
Examples:
{5,6,7,8} or { whole numbers less than 14}
In other words, the set has a stopping point…a
last value…a final number…doesn’t keep
going…finishes…no mas!
Note: The curly braces {} simply represent a set
of numbers…this is called “set notation.”
Infinite Sets
Infinite Sets have unlimited elements in their
set.
Examples:
{ 0, 1, 2, 3…} or {integers less than -3}
You can tell the difference between a finite and infinite
set based on whether the set keeps going, or whether
the set has a specific number of elements in it.
Always ask yourself: “Self, does this set keep going?”
If it does…then it’s infinite!
Cool huh?!
Empty Set
• The Empty Set is the set
that contains nothing. It
is called the null set.
• It is represented by
either
a { } or ø.
Venn Diagram
Real numbers
Rational Numbers
Integers
Whole
Irrational Numbers
Natural
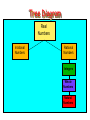
Tree Diagram
Real
Numbers
Irrational
Numbers
Rational
Numbers
Integers
Whole
Numbers
Natural
Numbers
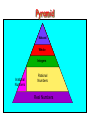
Pyramid
Natural
Whole
Integers
Irrational
Numbers
Rational
Numbers
Real Numbers
Nesting Boxes
Natural
Whole
Integers
Irrational
Numbers
Rational Numbers
Real Numbers
Summary
• Describe in your own words the
difference between rational and
irrational numbers
Homework: Worksheet