* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lesson 1: Classifying Real Numbers
Ethnomathematics wikipedia , lookup
History of logarithms wikipedia , lookup
Foundations of mathematics wikipedia , lookup
Law of large numbers wikipedia , lookup
Location arithmetic wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Infinitesimal wikipedia , lookup
Positional notation wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Bernoulli number wikipedia , lookup
Proofs of Fermat's little theorem wikipedia , lookup
Non-standard analysis wikipedia , lookup
Large numbers wikipedia , lookup
Surreal number wikipedia , lookup
Hyperreal number wikipedia , lookup
Real number wikipedia , lookup
Order theory wikipedia , lookup
Lesson 1: Classifying Real
Numbers
THE NUMBER SYSTEM
Warm up
1) A ______________ (Venn diagram, line plot) shows the relationship
between sets.
Write each fraction as a decimal.
2) 9
Write each decimal as a fraction in simplest form.
4) 0.6
2
3
3) 4 8
5) 5.75
New stuff: sets
A set is a collection of things.
In math when we talk about sets, we are talking about collections of
numbers.
Our number system is made up of these sets.
We name sets using a capital letter.
New stuff: sets
The things contained in sets are called elements
We use braces {} to denote sets.
There are three kinds of sets: finite sets, infinite sets, and the empty set.
Finite sets contain a finite number of elements: (e.g. A= {1, 2, 3, 6}
Infinite sets contain an infinite number of elements: (e.g. N={1, 2, 3, 4, 5, …}
The empty set contains no elements: { } or ∅
Subsets
For now, we are going to be working with a subset of the complex
numbers called the Real Numbers.
A subset is a set of numbers that is part of a larger set.
The next page shows the subsets of the Real Numbers.
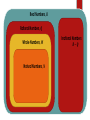
Subsets of Real Numbers
Natural Numbers 𝑁
The numbers we use to count things (these are also called the
counting numbers): 𝑁 = {1, 2, 3, 4, … }
Whole numbers 𝑊
All the natural numbers and zero: 𝑊 = {0, 1, 2, 3, … }
Integers 𝑍
The whole numbers and the opposites of the natural numbers:
𝑍 = {… , −3, −2, −1, 0, 1, 2, 3, … }
Rational numbers 𝑄
Numbers that can be written in the form 𝑏, where 𝑎 and 𝑏 are
integers and 𝑏 ≠ 0. In decimal form, rational numbers either
1
2
terminate or repeat. Examples: 2 , 0. 3, − 3 , 0.125
Irrational numbers 𝑅 − 𝑄
Numbers that can’t be written as the quotient of two integers.
Irrational numbers do NOT terminate or repeat in decimal form.
3
Examples: 5, 2, − 7, 3 3, 𝜋, 3𝜋, 𝑒
Real numbers 𝑅
The set including all rational and irrational numbers.
𝑎
Real Numbers, 𝑹
Rational Numbers, 𝑸
Whole Numbers, 𝑾
Natural Numbers, 𝑵
Irrational Numbers
𝑹−𝑸
Example 1: Identifying sets
For each number, identify the subset(s) of real numbers to which it belongs
A. 2
B. 5
C. 3 2
1
Example 2: Identifying sets for RealWorld Situations
Identify the set of numbers that best describes each situation. Explain your
choice.
A. the value of the bills in a person’s wallet
B. the balance of a checking account
C. the circumference of a circular table when the diameter is a rational
number
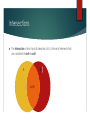
Intersections
The intersection of sets A and B, denoted 𝐴 ∩ 𝐵, is the set of elements that
are contained in both A and B
A
B
B
𝐴∩𝐵
Unions
The union of sets A and B, denoted 𝐴 ∪ 𝐵, is the set of all elements that are
in either A or B.
A
B
Example 3: Intersections and Unions of
Sets
Find 𝐴 ∩ 𝐵 and 𝐴 ∪ 𝐵.
a) 𝐴 = {2, 4, 6, 8, 10, 12}; 𝐵 = {3, 6, 9, 12}
b) 𝐴 = 11, 13, 15, 17 ; 𝐵 = {12, 14, 16, 18}
Closure
A set of numbers is closed, or has closure, under a given operation if the
outcome of the operation on any two members of the set is also a
member of the set.
For example, the sum of any two natural numbers is also a natural number.
Therefore, the set of natural numbers is closed under addition.
To prove a statement false, we just need to find one example. This is called
a counterexample.
Identifying a Closed Set Under a Given
Operation
Determine whether the statement is true of false. Give a counterexample
for false statements.
a) The set of whole numbers is closed under addition.
b) The set of whole numbers is closed under subtraction.
Lesson Practice
Let’s work a few more examples together. Be sure to put these in your
notebook.
Find 𝐶 ∩ 𝐷 and 𝐶 ∪ 𝐷.
g) 𝐶 = 4, 8, 12, 16, 20 ; D = {5, 10, 15, 20}
h) 𝐶 = 6, 12, 18, 24 ; 𝐷 = {7, 14, 21, 28}
Lesson Practice
Determine whether each statement is true or false. Provide a
counterexample for false statements.
i) The set of whole numbers is closed under multiplication.
j) the set of natural numbers is closed under division.
Homework
Start with the problems you think will be hardest. If you need help, put your
help card in the corner of the desk.
Pg. 5-6, #1-30.
Make sure you show any necessary work. You homework needs to be
neat. If you can’t fit all your work into the box, put it on a separate sheet of
paper and just put your answers in the box.
Remember, if I can’t hear the music, it’s too loud. This is an individual
activity. If you must communicate, you should be whispering.
We will be correcting this tomorrow. Make sure you have your red
correcting pens!