* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download pps (recommended)
List of types of proteins wikipedia , lookup
G protein–coupled receptor wikipedia , lookup
Magnesium transporter wikipedia , lookup
Protein phosphorylation wikipedia , lookup
Protein moonlighting wikipedia , lookup
Protein design wikipedia , lookup
Protein domain wikipedia , lookup
Protein (nutrient) wikipedia , lookup
Intrinsically disordered proteins wikipedia , lookup
Protein folding wikipedia , lookup
Circular dichroism wikipedia , lookup
Homology modeling wikipedia , lookup
Protein–protein interaction wikipedia , lookup
Structural alignment wikipedia , lookup
Proteolysis wikipedia , lookup
Nuclear magnetic resonance spectroscopy of proteins wikipedia , lookup
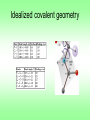
Protein Planes Bob Fraser CSCBC 2007 Overview • Motivation • Points to examine • Results • Further work Cα trace problem • Given: only approximate positions of the Cα atoms of a protein • Aim: Construct the entire backbone of the protein – This is an open problem! Cα trace problem • Why do it? • Some PDB files contain only Cα atoms. • Refinement of X-ray or NMR skeletons. • More importantly, many predictive approaches are incremental, and begin by producing the Cα trace. Cα trace problem • Possible solutions: – De novo, CHARMM fields (Correa 90) – Fragment matching (Levitt 92) – Maximize hydrogen bonding (Scheraga et al. 93) • Idealized covalent geometry – Used by Engh & Huber (91) for X-ray crystallography refinement – Supplemented by including additional information (Payne 93, Blundell 03) • All methods achieve <1Å rmsd, ~0.5Å rmsd is good. • Perhaps including more information about the plane could further improve results. Idealized covalent geometry The task • Survey the structures in the PDB, and determine how close the known structures adhere to these values. • Next look at the relationship between the planes and secondary structures – Is this information useful? – If so, could it be used in refinement? Length of plane (Cα – Cα distance) • The so-called bond distance when given a Cα trace. • If all bond angles and lengths are fixed, this distance should also be constant. • Let’s check this distance in the PDB, and determine the average, standard deviation, maximum and minimum values found. cis vs. trans Secondary Structure Angle between helix axis and plane • It is assumed that the planar regions for amino acids in a helix are parallel to the axis of the helix. • Let’s put this to the test! • How do we measure the axis of helix? – It is a subjective measure – We’ll use the method of Walther et al. (96), it provides a local helix axis Plane-axis angle • Now we have a peptide plane and the helix axis, so we can find the angle between them easily. • This same method could be applied to beta strands and 3-10 helices. • We should expect that some pattern should arise since beta strands are have regular patterns, particularly when in beta sheets. Data Analysis • Use the entire PDB database as a source • Compare the results obtained to the expected values for the plane lengths and alpha helices • Determine whether a preferential orientation exists for beta strands and 3-10 helices Plane length • trans and cis cases need to be distinguished because they are different inherently • Plane length is composed of 5 elements of idealized covalent geometry α-helix 3-10 Helix β-strand Results Future Work • Develop algorithm for using secondary structure to solve trace problem. • Test it on proteins with perfect Cα traces to verify the accuracy of reconstruction. • Test on randomized Cα traces. • Integrate this information with refinement Thanks! Selected References – M.A. DePristo, P.I.W. de Bakker, R.P. Shetty, and T.L. Blundell. Discrete restraint-based protein modeling and the C -trace problem. Protein Science, 12:2032-2046, 2003. – A. Liwo, M.R. Pincus, R.J. Wawak, S. Rackovsky, and H.A. Scheraga. Calculation of protein backbone geometry from alphacarbon coordinates based on peptide-group dipole alignment. Protein Sci., 2(10):1697-1714, 1993. – G.A. Petsko and D. Ringe. Protein Structure and Function. New Science Press Ltd, London, 2004. – D. Walther, F. Eisenhaber, and P. Argos. Principles of helix-helix packing in proteins: the helical lattice superimposition model. J.Mol.Biol., 255: 536-553, 1996. Walther axis calculation