Download Number Set Review #1 File

Numbers and Sets
A set is a collection of objects.
So, any collection of things, such as numbers, can be called a set.
To show that we have a set, we use brackets
To name a set we use capital letters.
{ }
A few others things to know about sets:



means is an element of.
means is NOT an element of.
or { } means the empty set and contains no elements.
For example:
Given the set A = {1, 2, 3, 4, 5, 6, 7}
we can say that
but
9 A
4 A
we would read this as “4 is an element of A”.
we would read this as “9 is not an element of A”.
A subset:
A set is a subset of another if every element in one set is also an element in
the other set.
To write this, we use the notation

For example:
Given P = {2, 3, 5} and Q = {1, 2, 3, 4, 5, 6}, then we can say that
PQ
this is read “P is a subset of Q.”
Intersection:
The intersection of two sets, or groups is the elements that both groups
have in common.
Here are two groups. What would the intersection of these groups
be?
A = {apples, oranges, pears}
B = {apples, plums, pears}
Answer: The intersection is {apples, pears}
The word AND is used to mean an intersection. You can also use the
symbol:
Union:
The union of two sets, or groups is the combination of the elements in
both groups. It doesn’t matter if they are in common or not.
Here are two groups. What would the union of these groups be?
A = {apples, oranges, pears}
B = {apples, plums, pears}
Answer: The union is {apples, oranges, pears, plums}
The word OR is used to mean a union. You can also use the symbol:
For example:
If P = {1, 3, 4} and Q = {2, 3, 5}, then:
P  Q  {1, 2, 3, 4, 5}
this is read “the union of P and Q is the
set 1, 2, 3, 4, 5.
P  Q  {3}
this is read “the intersection of P and Q
is the set 3.”
If P = {3, 5, 7} and Q = {1, 2, 3, 4, 5}, then:
P  Q  {1, 2, 3, 4, 5, 7}
this is read “the union of P and Q is the
set 1, 2, 3, 4, 5, 7.
P  Q {3, 5}
this is read “the intersection of P and Q
is the set 3 and 5.”
Given that M = {2, 3, 5, 7, 8, 9} and N = {3, 4, 6, 9, 10}:
Are the following true or false?
a) 4  M
b) 6  M
Answers:
a) False
b) True
Given that M = {2, 3, 5, 7, 8, 9} and N = {3, 4, 6, 9, 10}:
Give a list of the following.
Answers:
a) M  N
b) M  N
a) {3, 9}
b) {2, 3, 4, 5, 6, 7, 8, 9, 10}
Given that M = {2, 3, 5, 7, 8, 9} and N = {3, 4, 6, 9, 10}:
Are the following true or false?
Answers:
a) M  N
b) {9, 6, 3}  N
a) False
b) True
Number Sets
*
{1, 2, 3, 4, 5,...}  N
The set of all
Counting Numbers is
The set of all
Natural Numbers is {0, 1, 2, 3, 4, 5,...}  N
The set of all
Integers is {..., 3,  2,  1, 0, 1, 2, 3,...}  Z
The set of all
Positive Integers is
{1, 2, 3, 4, 5,...}  Z 
The set of all
Negative Integers is {1,  2,  3,  4,  5,...}  Z 
Rational Numbers -
Rational numbers can be written as the quotient
of integers.
Rational numbers can be written as decimals
that either repeat or end.
What does quotient mean?
What do we mean when we say that decimals either repeat or end?
{ qp where p and q are integers and q  0}  Q
Irrational numbers CANNOT be written as
quotients of integers.
Irrational Numbers Irrational numbers are decimals that continue forever
but do NOT repeat.
 Q'
Can you write down an example of an irrational number?
Some examples of irrational numbers are:
2,  ,  11
Real numbers are ALL of the different types of numbers
that you probably know right now.
Real Numbers There are other types of numbers but we will learn
about these later.
R
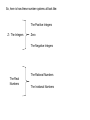
So, here is how these number systems all look like:
The Positive Integers
Z: The Integers
Zero
The Negative Integers
The Rational Numbers
The Real
Numbers
The Irrational Numbers
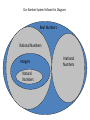
Our Number System Follows this Diagram:
Real Numbers
Rational Numbers
Integers
Natural
Numbers
Irrational
Numbers