Download Section 1.3 The Real Numbers

Math 123 Section 1.3 – The Real Numbers - Page 1
Section 1.3
The Real Numbers
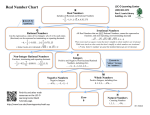
I. Sets and Set Notation
A. A set is a collection of objects.
B. The objects of a set are called the elements.
C. When a set is written in braces { }, with every element listed, it is written in roster
form.
D. Examples
1. A = {horses, pigs, cows}
2. B = {5, 10, 15}
a. We say that 5 is an element of set B and write it:
5∈ B
b. We say that 12 is not an element of set B and write it:
12 ∉ B
E. Definitions
1. A finite set is a set that has a definite number of elements.
2. An infinite set has an indefinite number of elements.
a. From above, A and B are finite sets.
b. C = {2, 4, 6, 8, . . .} is an infinite set.
3. The Natural Numbers or Counting Numbers is the set {1, 2, 3, . . .}
4. Note that if we wanted to write the set of the first 100 counting numbers, we
could write it as: {1, 2, 3, . . ., 100}.
5. The null set or empty set is the set with no elements. It is written:
∅
6. A set is written in set builder notation when it is written as a collection of
elements that must meet some rule to belong to the set. For example:
a. The set of all natural numbers greater than 4 would be written:
E = {x| x is a natural number > 4}
b. The set of natural numbers between 2 and 200 would be written:
F = {x| x is a natural number, 2 < x < 200}
7. A set G is a subset of a set H if every element of G is also in H. This is written:
G⊆H
8. The set of Whole Numbers is the set {0, 1, 2, 3, 4, . . .}
Note that the Natural Numbers are a subset of the Whole Numbers.
9. The Integers is the set {. . ., -3, -2, -1, 0, 1, 2, 3, . . .}. Note that both the Natural
Numbers and the Whole Numbers are a subset of the Integers.
10. The Rational Numbers is the set:
p

 | p, q ∈ Integers, q ≠ 0 
q


In other words, the rationals are the terminating and repeating decimals. Note that to
change a fraction to a decimal, you must divide the numerator by the denominator.
11. The Irrational Numbers are the set of all non-terminating, non-repeating decimals.
12. The Real Numbers is the union of the set of Rational and Irrational Numbers.
13. The number line is a line in which each point corresponds to a real number.
14. If a number m lies to the left of a number n on the number line, then we say that m < n,
which is read “m is less than n”.
15. If a number m lies to the right of a number n on the number line, then we say that m >
n, which is read “m is greater than n”.
16. The origin is 0.
17. The positive real numbers is the set {x: x > 0}. These are the numbers to the right of
the origin.
© Copyright 2009 by John Fetcho. All rights reserved
Math 123 Section 1.3 – The Real Numbers - Page 2
18. The negative real numbers is the set {x: x < 0}. These are the numbers to the left of
the origin.
19. The additive inverse or opposite of a real number is that number on the opposite side
of 0 as the number, but the same distance from 0. We write the opposite of a number p as
–p.
20. If x is a real number, then –(-x) = x . i.e. – A double negative gives a positive.
21. The absolute value of a number is the distance the number is from the origin.
F.
Examples - Graph each real number on a number line.
1.
5
Answer:
−5
−4
−3
−2
−1
0
1
2
3
4
5
−5
−4
−3
−2
−1
0
1
2
3
4
5
−1
0
1
2
3
4
5
3
4
5
3
4
5
2.
−2
Answer:
3.
Now you try one:
3
1
2
Answer:
−5
−4
−3
−2
1
3
2
7
3
Answer:
4.
−5
−4
−3
−2
−1
0
1
2
7
3
5.
Now you try one:
Answer:
−5
−4
−3
−1.8
−2
−1
0
1
2
−1.8
G. Examples – Simplify the following.
1. –(−35)
Answer: 35
2.
− − 11 = −(11)
Answer: −11
3. Now you try this one:
−8
Answer: −8
© Copyright 2009 by John Fetcho. All rights reserved
Math 123 Section 1.3 – The Real Numbers - Page 3
H. Examples – List the elements of the set.
1. A = {x: x is an integer divisible by 5}
Answer: A = {. . ., -10, -5, 0, 5, 10, . . .}
2. Now you try: B = {x: x is a natural number less than 10}
Answer: B = {1, 2, 3, 4, 5, 6, 7, 8, 9}
I. Examples – Write the set in set builder notation.
1. A = {3, 4, 5, 6, 7, 8}
Answer: A = {x|x is a natural number between 2 and 9}
2. Now you try: B = {2, 4, 6, . . . }
Answer: B = {x| x is a positive even integer}
J.
List all numbers from the set
{
}
1
−5.3, −5, − 3, −1, − ,0,1.2,1.8,3, 11
9
that are:
1.
2.
3.
Natural Numbers: {3}
Whole Numbers: {0, 3}
Integers: {−5, −1, 0, 3}
4.
Rational Numbers: {−5.3, −5, −1,
5.
Irrational Numbers:
{
B.
C.
D.
E.
}
9
3, 11
}
1
Real Numbers: −5.3, −5, − 3, −1, − ,0,1.2,1.8,3, 11
9
Inequalities
Not Equal
1.
The symbol that we use for not equal is ≠ .
2.
For example, 3 + 5 ≠ 10.
Less Than
1.
The symbol that we use for less than is <.
2.
For example, 3 + 5 < 10.
Greater Than
1.
The symbol that we use for greater than is >.
2.
For example, 10 > 3 + 5.
For both B & C, we could also have stated that the expression was < or >.
Examples - Insert either < or > in the blank between each pair of numbers to make a true
statement.
1.
2 _____ −4
The main thing to remember is that the larger number is always farther to the right on
the number line. Since any positive number is to the right of a negative number, we
have:
6.
II.
A.
{−
1
− , 0, 1.2, 1.8, 3}
Answer:
2 > −4
© Copyright 2009 by John Fetcho. All rights reserved
Math 123 Section 1.3 – The Real Numbers - Page 4
2.
3 _____ 2
On this one, we are getting a preview of coming attractions in this class!
What is the opposite of square root? Squaring of course! So if we square a square
root, we "undo" the square root. So squaring both sides, we get:
3 _____ 4
Since 3 is less than 4, we need to use the "<" sign.
Answer:
3.
3 <2
Now you try one:
Answer:
−π _____ −3.5
−π > −3.5
© Copyright 2009 by John Fetcho. All rights reserved