Download The Solar Radiation Budget, and High

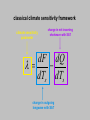
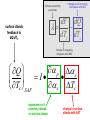
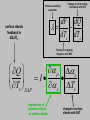
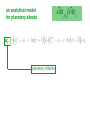
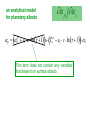
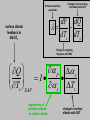
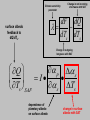
Narrowing the Divergence in
Simulations of Climate
Feedbacks
Alex Hall and Xin Qu
UCLA Department of Atmospheric and Oceanic
Sciences
Berkeley Atmospheric Science Symposium
October 14, 2005
Divergence in future climate simulations: This
plot shows the upper and lower limits of the
warming over the coming century predicted by
current GCM simulations.
This range is due to
two factors: (1)
uncertainty in
emissions scenarios
and (2) different
model sensitivities
(i.e. different
simulations of
climate feedbacks).
Equilibrium annual-mean response of a coarse resolution
climate model when surface albedo feedbacks are removed
all feedbacks present
no snow or ice albedo
feedback
Hall 2004
Simulated reduction in
reflected solar radiation
due to CO2 doubling
---Snow and sea ice albedo
feedbacks each account for
roughly half the total surface
albedo
feedback
in
the
northern hemisphere.
---Most of the snow albedo
feedback
comes
in
springtime, when both snow
cover and insolation are large.
(Hall, 2004)
---As we will see, there is a
factor of three divergence in
the overall strength of snow
albedo feedback in current
GCMs used in the IPCC AR4.
classical climate sensitivity framework
climate sensitivity
parameter
change in net incoming
shortwave with SAT
dF dQ


dTs dTs
change in outgoing
longwave with SAT
Climate sensitivity
parameter
Change in net incoming
shortwave with SAT
dF dQ


dTs dTs
surface albedo
feedback to
dQ/dTs.
Change in outgoing
longwave with SAT
Q 
 p  s


  I 
 s Ts
Ts SAF
dependence of
planetary albedo
on surface albedo
change in surface
albedo with SAT
In this talk, we explore a strategy
to reduce the divergence in IPCC
AR4 simulations of snow albedo
feedback. The idea is to split the
feedback
into
its
two
components and assess the
divergence in each separately.
The focus is on springtime, when
most of the snow albedo
feedback effect is concentrated.
Climate sensitivity
parameter
Change in net incoming
shortwave with SAT
dF dQ


dTs dTs
Change in outgoing
longwave with SAT
Q 
 p  s


  I 
 s Ts
Ts SAF
dependence of
planetary albedo
on surface albedo
change in surface
albedo with SAT
Climate sensitivity
parameter
Change in net incoming
shortwave with SAT
dF dQ


dTs dTs
surface albedo
feedback to
dQ/dTs.
Change in outgoing
longwave with SAT
Q 
 p  s


  I 
 s Ts
Ts SAF
dependence of
planetary albedo
on surface albedo
change in surface
albedo with SAT
THE ROLE OF CLOUD
To what extent do
clouds attenuate surface
albedo anomalies, and
hence weaken the
positive feedbacks
associated with the
cryosphere?
And how relevant are
cloud changes
associated with
anthropogenic climate
change in altering snow
and sea ice albedo
feedback?
How to estimate  p
 s?
Generating accurate estimates of p/s
from model output or from satellite data is
not straightforward, because of the
possibility that surface and cloud
variations could be correlated. This rules
out simply regressing planetary albedo
onto surface albedo.

 p  s
an analytical model
for planetary albedo
 p    1  c  ln  1 T  2  c  ln  1  s
cr
a
cr
a

The analytical model for planetary albedo gives
planetary albedo as a function of common
model output, such as cloud cover, cloud
optical thickness, and surface albedo. The
idea is to come up with an accurate analytical
expression for planetary albedo that can be
used to calculate a true partial derivative with
respect to surface albedo for any simulation or
satellite-derived data set.
Qu and Hall 2005
 p  s
an analytical model
for planetary albedo
 p    1  c  ln  1 T  2  c  ln  1  s
cr
a
cr
a

planetary albedo
 p  s
an analytical model
for planetary albedo
 p    1  c  ln  1 T  2  c  ln  1  s
cr
a
cr
a

contribution from atmosphere, composed
of a contribution from the clear-sky
atmosphere (effective albedo of the clearsky atmosphere), and a contribution from
cloud, proportional to the product of cloud
cover and the logarithm of cloud optical
thickness.
 p  s
an analytical model
for planetary albedo
 p    1  c  ln  1 T  2  c  ln  1  s
cr
a
cr
a

contribution from the surface, which is the surface
albedo modulated by two components: (1) the clearsky transmissivity of the atmosphere, and (2) the
cloudy sky transmissivity of the atmosphere,
proportional to the product of cloud cover and the
logarithm of cloud optical thickness
 p  s
The performance
analytical model…

of
the
…is extremely good. These
scatterplots show predicted
geographical and temporal
variability
in
springtime
planetary albedo values based
on input values required by
the analytical model (cloud
cover, cloud optical thickness, surface albedo, etc.)
against
actual
planetary
albedo variations in North
American and Eurasian land
masses. The analytical model
nearly
perfectly
captures
planetary albedo variability in
ISCCP as well as two current
simulations.
 p  s
an analytical model
for planetary albedo
 p    1  c  ln  1 T  2  c  ln  1  s
cr
a
cr
a

Because it captures observed and
simulated planetary albedo variations so
well, we can use the analytical model to
calculate a true partial derivative of
planetary albedo with respect to surface
albedo.
 p  s
an analytical model
for planetary albedo
 p    1  c  ln  1 T  2  c  ln  1  s
cr
a
cr
a

This term does not contain any variables
that depend on surface albedo.
 p  s
an analytical model
for planetary albedo
 p    1  c  ln  1 T  2  c  ln  1  s
cr
a
cr
a
 p cr
 Ta  2  c  ln   1
 s

attenuation effect of the clear-sky atmosphere on
surface albedo, represented by the clear-sky
atmospheric transmissivity
 p  s
an analytical model
for planetary albedo
 p    1  c  ln  1 T  2  c  ln  1  s
cr
a
cr
a
 p cr
 Ta  2  c  ln   1
 s

attenuation effect of clouds on surface albedo
anomalies, proportional to the product of cloud cover
and the logarithm of cloud optical thickness
Here is the contribution of the clear-sky atmosphere over both Eurasia
and North America in the transient climate change experiments with
current generation of models used in the IPCC AR4 assessment for
springtime. The calculation was done for the present climate (dark
green) and the climate 100 years from now (light green). The models
agree in this quantity to within a few percent. In a clear-sky
atmosphere, surface albedo anomalies typically result in planetary
albedo anomalies about 75% as large.
 p  s
 p
cr
 Ta  2  c  ln   1
 s
Here is the contribution of clouds
in springtime in the
same experiments.
There is substantially more intermodel
variability
than in the clear-sky
case,
with
the
models agreeing to
within about 20%.
 p  s
 p
cr
 Ta  2  c  ln   1
 s
Here is the sum of
the clear and cloud
sky contributions.
These also largely
converge,
mainly
because the clearsky component is
more than three
times as large as
the
cloudy-sky
component.
In
North America and
Eurasia, planetary
albedo
anomalies
are typically about
half as large as
associated surface
albedo anomalies.
 p  s
Climate sensitivity
parameter
Change in net incoming
shortwave with SAT
dF dQ


dTs dTs
surface albedo
feedback to
dQ/dTs.
Change in outgoing
longwave with SAT
Q 
 p  s


  I 
 s Ts
Ts SAF
dependence of
planetary albedo
on surface albedo
change in surface
albedo with SAT
Climate sensitivity
parameter
Change in net incoming
shortwave with SAT
dF dQ


dTs dTs
surface albedo
feedback to
dQ/dTs.
Change in outgoing
longwave with SAT
Q 
 p  s


  I 
 s Ts
Ts SAF
dependence of
planetary albedo
on surface albedo
change in surface
albedo with SAT
We can easily calculate
s/Ts
in
models by averaging
surface albedo and
surface
air
temperature values from
the beginning and end
of transient climate
change experiments.
Here is the evolution
of springtime Ts, snow
extent, and s in one
rep-resentative
experiment used in the
AR4 assessment.
 s Ts
Hall and Qu 2005
We can easily calculate
s/Ts
in
models by averaging
surface albedo and
surface
air
temperature values from
the beginning and end
of transient climate
change experiments.
Here is the evolution
of springtime Ts, snow
extent, and s in one
rep-resentative
experiment used in the
AR4 assessment.
 s Ts
Ts
s
 p  s

While
there
is
convergence for the
most
part
in
simulations of the dependence of planetary
albedo on surface
albedo, the sensitivity
of surface albedo to
surface
air
temperature
exhibits
a
three-fold spread in
the current generation
of climate models.
This is likely due to
differing
surface
albedo
parameterizations.
 s Ts
HOW TO REDUCE THIS DIVERGENCE?
The work of Tsushima et al. (2005) and Knutti and
Meehl (2005) suggests the seasonal cycle of
temperature may be subject to the same climate
feedbacks as anthropogenic warming. Therefore
comparing simulated feedbacks in the context of
the seasonal cycle to observations may offer a
means of circumventing a central difficulty of
future climate research: It is impossible
to
evaluate future climate feedbacks against
observations that do not exist.
 s Ts
calendar month
In the case of snow albedo feedback, the seasonal cycle may be a particularly
appropriate analog for climate change because the interactions of northern
hemisphere continental temperature, snow cover, and broadband surface albedo in
the context of the seasonal variation of insolation are strikingly similar to the
interactions of these variables in the context of anthropogenic forcing.
 s Ts
April Ts
April s
calendar month
 s Ts
May Ts
May s
calendar month
 s Ts
Ts
s
calendar month
So we can calculate springtime values of s/Ts for
climate change and the current seasonal cycle.
What is the relationship between this feedback
parameter in these two contexts?
Intermodel
variations
in
s/Ts in the seasonal cycle
context are highly correlated
with s/Ts in the climate
change
context,
so
that
models exhibiting a strong
springtime
SAF
in
the
seasonal cycle context also
exhibit a strong SAF in
anthropogenic climate change.
Moreover, the slope of the
best-fit regression line is
nearly one, so values of
s/Ts based on the presentday seasonal cycle are also
excellent predictors of the
absolute magnitude of s/Ts
in the climate change context.
 s Ts
observational
estimate based
on ISCCP
 s Ts
It’s possible to calculate an
observed value of s/Ts in
the seasonal cycle context
based on the ISCCP data set
(1984-2000) and the ERA40
reanalysis.
This value falls
near the center of the model
distribution.
observational
estimate based
on ISCCP
95%
confidence
interval
 s Ts
It’s also possible to calculate
an estimate of the statistical
error in the observations,
based on the length of the
ISCCP
time
series.
Comparison to the simulated
values shows that most
models
fall
outside
the
observed range.
However, the observed error
range may not be large enough
because of measurement error
in the observations.
Conclusions, Part I
 p  s
To within 10%, surface albedo anomalies over the NH land masses
result in planetary albedo anomalies about half as large in climate
simulations and in the satellite-based ISCCP data set.
This
component of snow albedo feedback is therefore not a main source
of divergence in climate simulations.
Conclusions, Part II
 s Ts
On the other hand the sensitivity of surface albedo to surface
temperature in NH land masses exhibits a factor-of-three spread
in transient climate change experiments. This spread may be
dramatically reduced by exploiting the northern hemisphere
springtime warming and simultaneous snow retreat as an analog
for anthropogenic climate change. Large intermodel variations in
snow albedo feedback's strength in human-induced climate
change are nearly perfectly correlated with comparably large
intermodel variations in its strength in the context of the presentday seasonal cycle.
Conclusions, Part III
We compared snow albedo feedback's strength in the real
seasonal cycle to simulated values. They mostly fall well
outside the range of the observed estimate, suggesting many
models have an unrealistic snow albedo feedback. Though
this comparison may put the models in an unduly harsh light
because of uncertainties in the observed estimate that are
difficult to quantify, these results map out a clear strategy for
targeted climate system observation and analysis to reduce
divergence in climate sensitivity.
Identifying and correcting model biases in simulations of
snow albedo feedback in the current seasonal cycle will lead
directly to a reduction in the spread of simulations of snow
albedo feedback in anthropogenic climate change.