Download Alg1_1.6_Rational Part 1

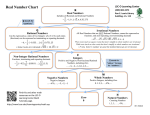
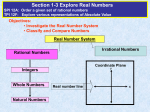
Rational Numbers: Part 1
Section 1.6
Types of numbers:
•
•
•
•
•
Natural = The numbers you naturally count.
Whole = Natural numbers and zero
Integers = Positive and negative whole numbers
Rational = Numbers that can be written as a ratio
Irrational = Numbers than cannot be written as a
ratio (fraction between integers)
• Real numbers = All rational & irrational numbers
• Imaginary numbers = Signified by “i”
Square root of a negative number
2
Decimals
• Some decimals are rational numbers.
• Decimals that are “terminating” or
“repeating” are rational numbers.
• Terminating = A decimal that has an end
.4 .88 .125
• Repeating = A decimal that repeats the
same sequence of numbers forever.
Comparing Rational Numbers
Same denominator: put the numerators in order:
⅛ ⅜ ⅝ ⅞
Smallest
Largest
•Convert fractions into decimals, if they do
not have the same denominator.
4
Greater than or Less than?
Remember negative
whole numbers:
4 > 2 but -4 < -2
>
Convert to decimal if you aren’t sure:
-.125
-.500
Put fractions in order,
least to greatest
A larger numerator or denominator does not
necessarily mean the fraction is larger.
In notebook:
1) Put the following fractions in order
from least to greatest:
2) Put the following in order from least
to greatest:
-3.3, -3⅓, -3.09
3) Which is greater, 4⅜ or 4.35?
7
Homework: pg 32-34
(1-8 all, 25-28 all, 35, 42-45 all)
8