Download Bell Ringer

Bell Ringer
Replace each ___ with <, >, or = to make a true
sentence.
#1.
#2.
#3.
#4.
Things I Need to Give You

New Homework Sheet
 Make
sure you picked this up. We are starting over new this
9 weeks so even if you still have the bottom half of the last
week’s, use this one – brand new – starting at the top!

Bathroom Passes
 Each
person should have 6. MAKE SURE YOU WRITE YOUR
NAME ON THEM NOW!!!

Fraction – Decimal Equivalent Chart
 This
was from yesterday’s lesson. It needs to be memorized
for quizzes.
NOTICE

First quiz will be on THURSDAY, OCT 16.
 It
will cover Sections 3.1, 3.2, and 10.1
Homework Check from Last Night
Homework Check from Last Night
Section 3.2
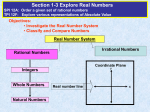
Rational Numbers
R drive > Key > Week 10 > Tuesday >
3.2 PowerPoint
File > Save As > P Drive > Math > Week 10 >
3.2 PowerPoint
Vocabulary





Natural Numbers – Numbers in the set {1, 2, 3, …}.
Represented by N.
Whole Numbers – The set of natural numbers plus zero
{0, 1, 2, 3,…}. Represented by W.
Integers – Whole numbers and their opposites
{… -3, -2, -1, 0, 1, 2, 3,…}. Represented by Z.
Rational Numbers – Any number that can be
written as a fraction. Represented by Q.
Irrational Numbers – Decimals that neither
terminate or repeat.
Notes





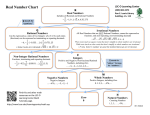
Numbers like 1, 0, -3, and 1½ can be organized into
sets.
When you first learned to count using the numbers
1,2,3,… you were using members of the set of natural
numbers, N = {1, 2, 3, …}
If you add zero to the set of natural numbers, the result
is the set of whole numbers, W = {0, 1, 2, 3…}
Whole numbers and their opposites make up the set of
integers, Z = {…-3, -2, -1, 0, 1, 2, 3, …}
Any number that can be written as a fraction is part of
the set of rational numbers, Q. Some examples of
rational numbers are 0.87, -23, 2/3, -2.56, 1½
Notes
Fractions, mixed numbers, and integers
are all rational numbers. Terminating
decimals are also rational numbers
because they can be written as fractions
with a denominator of 10, 100, 1000,
and so on. Any repeating decimal can
be written as a fraction, so repeating
decimals are rational numbers.
Notes
Example 1
Write Mixed Numbers and Integers as Fractions
Example 2
Write Mixed Numbers and Integers as Fractions
Write each rational number as a fraction.
a.
b. 10
Your Turn
Practice Writing Mixed Numbers and Integers as Fractions
Example 3
Write Terminating Decimals as Fractions
Example 4
Write Terminating Decimals as Fractions
a.
b.
Write 0.26 as a fraction in simplest form.
The shipping weight of a package is 2.875
pounds. Write this decimal as a mixed number in
simplest form.
Your Turn
Practice Writing Terminating Decimals as Fractions
Example 5
Write Repeating Decimals as Fractions
Example 6
Write Repeating Decimals as Fractions
Write 0.39 as a fraction in simplest form.
Your Turn
Practice Writing Repeating Decimals as Fractions
Example 7
Classify Numbers
Example 8
Classify Numbers
Identify all sets to which each number belongs.
a.
b. 1.414213562…
c. 15
Homework
Section 3.2 #1-10