Download Prezentacja programu PowerPoint

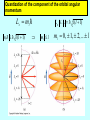
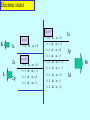
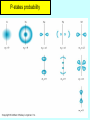
Lecture V
Hydrogen Atom
dr hab. Ewa Popko
Niels Bohr
1885 - 1962
Bohr Model of the Atom
• Bohr made three assumptions (postulates)
• 1. The electrons move only in certain circular orbits, called
STATIONARY STATES. This motion can be described
classically
• 2. Radiation only occurs when an electron goes from one
allowed state to another of lower energy.
• The radiated frequency is given by
hf = Em - En
where Em and En are the energies of the two states
• 3. The angular momentum of the electron is restricted to
integer multiples of h/ (2p) = 
mevr = n  (1)
The hydrogen atom
The Schrödinger equation
Hˆ  x, y, z  = E x, y, z 


2
 2 
 2   2









V
x
,
y
,
z

  x, y, z  = E  x, y, z 
2
2
2 

y
z 


 2m  x

Partial differential equation with three independent variables
The potential energy in
spherical coordinates
(The potential energy
function is spherically
symmetric.)
1 e2
V (r ) = 
4p 0 r
The spherical
coordinates
(alternative to
rectangular coordinates)
The hydrogen atom
For all spherically symmetric potential-energy functions:
( the solutions are obtained by a method called separation of variables)
 ( x, y, z )   r , ,  = Rnl r Ylm  ,  = Rnl r  l ,m ( ) m ( )
l
Radial function
Angular function of  and 
Thus the partial differential equation with three independent variables
three separate ordinary differential equations
The functions  and  are the same for every spherically
symmetric potential-energy function.
l
The solution
The solution is determined by boundary conditions:
- R(r) must approach zero at large r (bound state electron localized near the nucleus);
  and  must be periodic:
(r,, and (r,,2p describe the same point, so
=2p;
  and  must be finite.
Quantum numbers:
n - principal
l – orbital
ml - magnetic
Principal quantum number: n
The energy En is determined by n = 1,2,3,4,5,…;
Ionized atom
 e4
1
En = 
 2
2 2 2
32p  0  n
n=3
- 3.4 eV
1
En = 13.6eV  2
n
  reduced mass
me mN
=
me  m N
E = - 13.6 eV
n=2
n=1
Quantization of the orbital angular momentum.
The possible values of the magnitude L of the orbital angular
momentum L are determined by the requirement, that the  function
must be finite at =0 and =p.
L =  l (l  1) l = 0, 1, 2, ... Orbital quantum number

There are n different possible values of L for the n th energy level!
Quantization of the component of the orbital angular
momentum
Lz = ml 
ml    l (l  1)

Lz  L =  l (l  1)
ml  l
ml = 0,  1,  2, ... l
Quantum numbers: n, l, m
n – principal quantum number
n – determines permitted values of the energy
n = 1,2,3,4...
l – orbital quantum number
l - determines permitted values of the orbital
angular momentum
l = 0,1,2,…n-1;
ml - magnetic quantum number
ml – determines permitted values of the z-component
of the orbital angular momentum
ml = 0,  1,  2, ...  l
Wave functions
n=1
l=0
n,l,m
n=2
 r , ,  = Rnl r  l ,m ( ) m ( )
l
l
l = 0,1
R( r ) ~ e
r
  polynomial
 ~
e

 i
l = 1 m = ±1
n=3
l = 0,1,2
Quantum number notation
Degeneracy : one energy level En has different
quantum numbers l and ml
l = 0 : s states
n=1 K shell
l = 1 : p states
n=2 L shell
l = 2 : d states
n=3 M shell
l = 3 : f states
n=4 N shell
l = 4 : g states
n=5 O shell
.
.
.
.
Electron states
K
1s
2s
L
n =1
l = 0 & ml = 0
n=2
l = 0 & ml = 0
l = 1 & ml =  1
2p
l = 1 & ml = 0
l = 1 & ml = 1
n=3
l = 0 & ml = 0
3s
l = 1 & ml =  1
l = 1 & ml = 0
l = 1 & ml = 1
3p
l = 2 & ml =  2
M
l = 2 & ml =  1
l = 2 & ml = 0
l = 2 & ml = 1
l = 2 & ml = 2
3d
S-states probability
P-states probability
Spin angular momentum and
magnetic moment
Electron posseses spin angular momentum Ls. With this momentum
magnetic momentum is connected:
e 
 s =  Ls
me

e 
s =  ge
Ls
2me

where ge is the gyromagnetic ratio
For free electron ge=2
Spin
angular
Własny
momentmomentum
pędu - spin and
magnetic moment
Allowed values of the spin angular momentum are quantized :
Ls =  s( s  1)
spin quantum number s = ½
Ls = 
3
2
The z – component of the spin angular momentum:
Lsz = ms 
 1
 2
ms = 
 1
 2
To label completely the state of the electron in a
hydrogen atom, 4 quantum numbers are need:
name
label
magnitude
Principal
quantum
number
Orbital
quantum
number
magnetic
quantum
number
Spin
quantum
number
n
1, 2, 3, ...
l
0, 1, 2, ... n-1
ml
ms
od –l do +l
± 1/2
Many – electron atoms and the exclusion
principle

Central field approximation:
- Electron is moving in the total electric field due to the nucleus and
averaged – out cloud of all the other electrons.
- There is a corresponding spherically symmetric potential – energy
function U( r).
Solving the Schrodinger equation the same 4 quantum numbers are
obtained. However wave functions are different. Energy levels depend
on both n and l.
• In the ground state of a complex atom the electrons cannot all be in
the lowest energy state.
Pauli’s exclusion principle states that no two electrons can
occupy the same quantum – mechanical state. That is, no
two electrons in an atom can have the same values of all four
quantum numbers (n, l, ml and ms )
Shells and orbitals
n
1
shell
K
l
orbital
0
s
2
L
0
s
L
1
p
M
M
M
N
N
N
N
0
1
2
0
1
2
3
s
p
d
s
p
3
4
d
f
Nmax - maximum number of electrons occupying given orbital
Nmax
2
2
6
2
6
10
2
6
10
14
Shells K, L, M
n
1
2
l
0
0
ml
0
0
3
1
-1
0
0
1
0
1
-1
0
2
1
-2
-1
0
1
2
ms
N
2
8
18
N : number of allowed states
state with ms = +1/2
state with ms = -1/2
Hund’s rule - electrons occupying given shell initially set up
their spins paralelly
carbon


oxygen


1s22s22p2

1s22s22p4
The periodic table of elements
Atoms of helium, lithium and sodium
n =3, l = 0
3s
n =2, l = 1
n =2, l = 1
2p
n =2, l = 0
n =2, l = 0
n =2, l = 0
2s
n =1, l = 0
n =1, l = 0
n =1, l = 0
1s
Helium (Z = 2)
Lithium(Z = 3)
Sodium (Z= 11)
Electron configuration – the occupying of orbitals
1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2 4f14
5d10 6p6 7s2 6d10 5f14
K : 1s 2  3 p 6 4 s1
Ca :
3 p 6 4s 2
Sc :
3d 1 4 s 2
Ti :
3d 2 4 s 2
V:
3d 3 4 s 2
Cr :
3d 5 4 s1
Mn:
3d 5 4 s 2
Cu :
3d 10 4 s1
Total angular momentum - J
  
J = L  LS

J =
j  j  1
Possible two magnitudes of j :
J z = m j ,
j = l  s or j = l-s
m j =  j, j  1,, j  1, j
Example: l = 1, s = ½
j = 1  12 =
3
2
lub
j = 1  12 =
1
2
m j =  23 , 12 , 12 , 23 lub m j =  12 , 12
j = 3/2
j = 1/2
NMR ( nuclear magnetic resonance)
Like electrons, protons also posses magnetic moment due to
orbital angular momentum and spin ( they are also spin-1/2
particles) angular momentum.
Spin flip experiment:
Protons, the nuclei of hydrogen atoms in the tissue under study,
normally have random spin orientations. In the presence of a
strong magnetic field, they become aligned with a component
paralell to the field. A brief radio signal flips the spins; as their
components reorient paralell to the field, they emit signals that
are picked up by sensitive detectors. The differing magnetic
environment in various regions permits reconstruction of an
image showing the types of tissue present.