GPS semester review
... a. electrons, protons, and nuclei c. protons, neutrons, and nuclei b. elements, protons, and electrons d. protons, neutrons, and electrons ____ 137. In an atom, electrons ____. a. are located in the nucleus c. travel outside the nucleus b. are paired with neutrons d. are always in the same place in ...
... a. electrons, protons, and nuclei c. protons, neutrons, and nuclei b. elements, protons, and electrons d. protons, neutrons, and electrons ____ 137. In an atom, electrons ____. a. are located in the nucleus c. travel outside the nucleus b. are paired with neutrons d. are always in the same place in ...
Chapter 5 | Molecular Orbitals
... l inear combinations of atomic orbitals (LCAO) , the sums and differences of the atomic wave functions. For diatomic molecules such as H2, such wave functions have the form = caca + cbcb here is the molecular wave function, ca and cb are atomic wave functions for atoms w a an ...
... l inear combinations of atomic orbitals (LCAO) , the sums and differences of the atomic wave functions. For diatomic molecules such as H2, such wave functions have the form = caca + cbcb here is the molecular wave function, ca and cb are atomic wave functions for atoms w a an ...
AP Chemistry-midterm review
... ____ 51. Heating MgSO4•7H2O at 150 C produces MgSO4•xH2O. If heating 24.4 g of pure MgSO4•7H2O at 150 C were to give 13.7 g of pure MgSO4•xH2O, calculate the value for x. a. 5 b. 4 c. 3 d. 2 e. 1 ____ 52. An ore of lead is 45.0% pure lead sulfide, PbS, and 55.0% impurities in which no other lead com ...
... ____ 51. Heating MgSO4•7H2O at 150 C produces MgSO4•xH2O. If heating 24.4 g of pure MgSO4•7H2O at 150 C were to give 13.7 g of pure MgSO4•xH2O, calculate the value for x. a. 5 b. 4 c. 3 d. 2 e. 1 ____ 52. An ore of lead is 45.0% pure lead sulfide, PbS, and 55.0% impurities in which no other lead com ...
Entanglement Theory and the Quantum
... problems. We then present a negative result on the usefulness of quantum computers in determining the ground-state energy of local Hamiltonians: Even under the promise that the spectral gap of the Hamiltonian is larger than an inverse polynomial in the number of sites, already for one-dimensional Ha ...
... problems. We then present a negative result on the usefulness of quantum computers in determining the ground-state energy of local Hamiltonians: Even under the promise that the spectral gap of the Hamiltonian is larger than an inverse polynomial in the number of sites, already for one-dimensional Ha ...
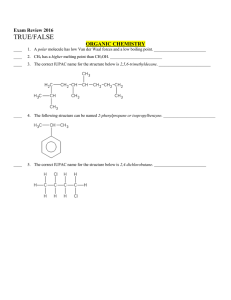
Multiple Choice Exam Review June 2016
... ____ 12. The shape of SO2 is trigonal planar. ____________________ ____ 13. The valence p orbitals in phosphorus, P, are half-filled. ____________________ ____ 14. All of the valence electrons in Fe2+ must have the same spin. _________________________ ____ 15. The shape of boron trifluoride, BF3, is ...
... ____ 12. The shape of SO2 is trigonal planar. ____________________ ____ 13. The valence p orbitals in phosphorus, P, are half-filled. ____________________ ____ 14. All of the valence electrons in Fe2+ must have the same spin. _________________________ ____ 15. The shape of boron trifluoride, BF3, is ...
The electronic properties of graphene
... efit of hindsight, no experimental tools existed to search for one-atom-thick flakes among the pencil debris covering macroscopic areas 共Geim and MacDonald, 2007兲. Graphene was eventually spotted due to the subtle optical effect it creates on top of a chosen SiO2 substrate 共Novoselov et al., 2004兲 t ...
... efit of hindsight, no experimental tools existed to search for one-atom-thick flakes among the pencil debris covering macroscopic areas 共Geim and MacDonald, 2007兲. Graphene was eventually spotted due to the subtle optical effect it creates on top of a chosen SiO2 substrate 共Novoselov et al., 2004兲 t ...
physical setting chemistry
... carefully, tear off your answer sheet and fill in the heading. Your answer booklet for Part B–2 and Part C is stapled in the center of this examination booklet. Open the examination booklet, carefully remove your answer booklet, and close the examination booklet. Then fill in the heading of your ans ...
... carefully, tear off your answer sheet and fill in the heading. Your answer booklet for Part B–2 and Part C is stapled in the center of this examination booklet. Open the examination booklet, carefully remove your answer booklet, and close the examination booklet. Then fill in the heading of your ans ...
Lecture 04 10 Sep 13 - MSU Engineering
... Count carriers nS available for current – Pr. 1.3 (1-DEG) How nS influences scattering in unexpected ways – Pr 1.1 (2-DEG) One dimensional electron gas (1-DEG) Special Schrödinger eqn (Con E) that accommodates: Electronic confinement: band bending due to space charge Useful external B-field ...
... Count carriers nS available for current – Pr. 1.3 (1-DEG) How nS influences scattering in unexpected ways – Pr 1.1 (2-DEG) One dimensional electron gas (1-DEG) Special Schrödinger eqn (Con E) that accommodates: Electronic confinement: band bending due to space charge Useful external B-field ...
Perspective: Fifty years of density-functional theory in chemical physics
... somehow contained in the total electron density alone, is so compelling it can drive one mad. I attended my first DFT conference in 1983, a two week NATO workshop in Alcabideche, Portugal.1 The intensity of the debates and the level of scientific excitement at the meeting were impressive. I was hook ...
... somehow contained in the total electron density alone, is so compelling it can drive one mad. I attended my first DFT conference in 1983, a two week NATO workshop in Alcabideche, Portugal.1 The intensity of the debates and the level of scientific excitement at the meeting were impressive. I was hook ...