PDF
... umbrella of the correspondence principle or postulate. The latter states that a correspondence exists between certain classical and quantum operators, (such as the Hamiltonian operators) or algebras (such as Lie or Poisson (brackets)), with the classical ones being in the real (R) domain, and the qu ...
... umbrella of the correspondence principle or postulate. The latter states that a correspondence exists between certain classical and quantum operators, (such as the Hamiltonian operators) or algebras (such as Lie or Poisson (brackets)), with the classical ones being in the real (R) domain, and the qu ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI-600034 M.Sc. Part-A NOVEMBER 2015
... zero point energy of H79Br. Use the method of separation of variables to break up Schrodinger equation for a rigid rotor into ordinary angular equations and write the solutions for each. Show that for a 1s orbital of a hydrogen like ion, the most probable distance from the nucleus to electron is ao/ ...
... zero point energy of H79Br. Use the method of separation of variables to break up Schrodinger equation for a rigid rotor into ordinary angular equations and write the solutions for each. Show that for a 1s orbital of a hydrogen like ion, the most probable distance from the nucleus to electron is ao/ ...
Lecture #3
... A moving “particle” is described by a superposition of a great many sin and cos waves which constructively interfere to give a Gaussian probability near a certain point but destructively interfere everywhere else. The Gaussian “wave packet” moves according to the kinetic energy given by the average ...
... A moving “particle” is described by a superposition of a great many sin and cos waves which constructively interfere to give a Gaussian probability near a certain point but destructively interfere everywhere else. The Gaussian “wave packet” moves according to the kinetic energy given by the average ...
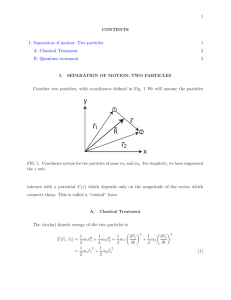
Physical Chemistry The hydrogen atom Center of mass
... One incorporates spin as a separate coordinate Wave function is a product n ,l ,m , I ,mI (r , , ) ...
... One incorporates spin as a separate coordinate Wave function is a product n ,l ,m , I ,mI (r , , ) ...
E3570: A particle on a disc with a homogeneous magnetic... levels
... E3570: A particle on a disc with a homogeneous magnetic field - Landau levels Submitted by: Roee Enbar & Gil Sharon The problem: A particle is bound to move on the XY plane in the presence of a homogeneous magnetic field perpendicular to the plane. (1) Write the Hamiltonian in Cartesian coordinates. ...
... E3570: A particle on a disc with a homogeneous magnetic field - Landau levels Submitted by: Roee Enbar & Gil Sharon The problem: A particle is bound to move on the XY plane in the presence of a homogeneous magnetic field perpendicular to the plane. (1) Write the Hamiltonian in Cartesian coordinates. ...
Homework No. 01 (Spring 2016) PHYS 530A: Quantum Mechanics II
... where v = dx/dt is the velocity in the x direction. (a) Find the Lagrangian for this system that implies the equation of motion of Eq. (1) using Hamilton’s principle of stationary action. (b) Determine the canonical momentum for this system (c) Determine the Hamilton H(p, x) for this system. 2. (10 ...
... where v = dx/dt is the velocity in the x direction. (a) Find the Lagrangian for this system that implies the equation of motion of Eq. (1) using Hamilton’s principle of stationary action. (b) Determine the canonical momentum for this system (c) Determine the Hamilton H(p, x) for this system. 2. (10 ...
Nonlincourse13
... The similarity to the classical case is reassuring. Only off-diagonal ("nonresonant") terms can be eliminated by a nonsingular transformation. The resulting Hamiltonian is diagonal, but nonlinear. The generator of the transformation is determined up to a diagonal ("resonant") term. This procedure ca ...
... The similarity to the classical case is reassuring. Only off-diagonal ("nonresonant") terms can be eliminated by a nonsingular transformation. The resulting Hamiltonian is diagonal, but nonlinear. The generator of the transformation is determined up to a diagonal ("resonant") term. This procedure ca ...
Lecture 2 Hamiltonian operators for molecules CHEM6085: Density
... • The Born-Oppenheimer approximation is based on the fact that nuclei have much larger masses than the electrons • To a good approximation, one can solve the Schrödinger equation only for the electrons and assume the nuclei are frozen • We will use this approximation from now on • As a result, our w ...
... • The Born-Oppenheimer approximation is based on the fact that nuclei have much larger masses than the electrons • To a good approximation, one can solve the Schrödinger equation only for the electrons and assume the nuclei are frozen • We will use this approximation from now on • As a result, our w ...
4.4 The Hamiltonian and its symmetry operations
... This is the adequate description of the state of a system described by the Hamiltonian H. This representation allows to calculate the time evolution easily. REMARK: This is just one example in natural science where discussing the symmetries serve fundamental information on the system. The search for ...
... This is the adequate description of the state of a system described by the Hamiltonian H. This representation allows to calculate the time evolution easily. REMARK: This is just one example in natural science where discussing the symmetries serve fundamental information on the system. The search for ...
another Exam2
... n = 2 states due to this electric field. (Give your answers in terms of e , E0 , a0 , etc.) (b) (10) Calculate the 4 energy eigenstates as superpositions of the original unperturbed states 200 , 210 , 211 , and 21, !1 . (I.e., if the new states are labeled 1 , 2 , 3 , 4 , you might obtain solutions ...
... n = 2 states due to this electric field. (Give your answers in terms of e , E0 , a0 , etc.) (b) (10) Calculate the 4 energy eigenstates as superpositions of the original unperturbed states 200 , 210 , 211 , and 21, !1 . (I.e., if the new states are labeled 1 , 2 , 3 , 4 , you might obtain solutions ...
3.5 Why does a quantum mechanic state change?
... REMARK: Principally you do not need superconductivity to find zero ohmic resistance; once a current flow started (described by the k-distribution of electrons, which are Eigenstates of the Hamiltonian) it would be stable for infinite time. You need defects within the crystal or phonons to reduce the ...
... REMARK: Principally you do not need superconductivity to find zero ohmic resistance; once a current flow started (described by the k-distribution of electrons, which are Eigenstates of the Hamiltonian) it would be stable for infinite time. You need defects within the crystal or phonons to reduce the ...
3.2 Conserved Properties/Constants of Motion
... only the phase changes as a function of time. A successive measurement will find always the same Eigenvalue. The energy and the expectation value of the operator A are thus always measurable at the same time. The state of as system is defined completely if all expectation values of those operators a ...
... only the phase changes as a function of time. A successive measurement will find always the same Eigenvalue. The energy and the expectation value of the operator A are thus always measurable at the same time. The state of as system is defined completely if all expectation values of those operators a ...