* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Prezentacja programu PowerPoint
Quantum computing wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Probability amplitude wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Scalar field theory wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
Nitrogen-vacancy center wikipedia , lookup
Tight binding wikipedia , lookup
Quantum machine learning wikipedia , lookup
Quantum teleportation wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Renormalization wikipedia , lookup
Quantum key distribution wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Matter wave wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Quantum group wikipedia , lookup
Wave function wikipedia , lookup
Bell's theorem wikipedia , lookup
Electron scattering wikipedia , lookup
Renormalization group wikipedia , lookup
Wave–particle duality wikipedia , lookup
Hidden variable theory wikipedia , lookup
History of quantum field theory wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Particle in a box wikipedia , lookup
EPR paradox wikipedia , lookup
Canonical quantization wikipedia , lookup
Spin (physics) wikipedia , lookup
Quantum state wikipedia , lookup
Ferromagnetism wikipedia , lookup
Atomic theory wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Atomic orbital wikipedia , lookup
Electron configuration wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
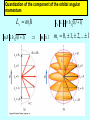
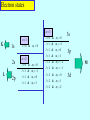
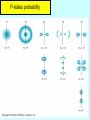
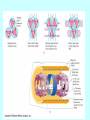
Lecture V Hydrogen Atom dr hab. Ewa Popko Niels Bohr 1885 - 1962 Bohr Model of the Atom • Bohr made three assumptions (postulates) • 1. The electrons move only in certain circular orbits, called STATIONARY STATES. This motion can be described classically • 2. Radiation only occurs when an electron goes from one allowed state to another of lower energy. • The radiated frequency is given by hf = Em - En where Em and En are the energies of the two states • 3. The angular momentum of the electron is restricted to integer multiples of h/ (2p) = mevr = n (1) The hydrogen atom The Schrödinger equation Hˆ x, y, z = E x, y, z 2 2 2 2 V x , y , z x, y, z = E x, y, z 2 2 2 y z 2m x Partial differential equation with three independent variables The potential energy in spherical coordinates (The potential energy function is spherically symmetric.) 1 e2 V (r ) = 4p 0 r The spherical coordinates (alternative to rectangular coordinates) The hydrogen atom For all spherically symmetric potential-energy functions: ( the solutions are obtained by a method called separation of variables) ( x, y, z ) r , , = Rnl r Ylm , = Rnl r l ,m ( ) m ( ) l Radial function Angular function of and Thus the partial differential equation with three independent variables three separate ordinary differential equations The functions and are the same for every spherically symmetric potential-energy function. l The solution The solution is determined by boundary conditions: - R(r) must approach zero at large r (bound state electron localized near the nucleus); and must be periodic: (r,, and (r,,2p describe the same point, so =2p; and must be finite. Quantum numbers: n - principal l – orbital ml - magnetic Principal quantum number: n The energy En is determined by n = 1,2,3,4,5,…; Ionized atom e4 1 En = 2 2 2 2 32p 0 n n=3 - 3.4 eV 1 En = 13.6eV 2 n reduced mass me mN = me m N E = - 13.6 eV n=2 n=1 Quantization of the orbital angular momentum. The possible values of the magnitude L of the orbital angular momentum L are determined by the requirement, that the function must be finite at =0 and =p. L = l (l 1) l = 0, 1, 2, ... Orbital quantum number There are n different possible values of L for the n th energy level! Quantization of the component of the orbital angular momentum Lz = ml ml l (l 1) Lz L = l (l 1) ml l ml = 0, 1, 2, ... l Quantum numbers: n, l, m n – principal quantum number n – determines permitted values of the energy n = 1,2,3,4... l – orbital quantum number l - determines permitted values of the orbital angular momentum l = 0,1,2,…n-1; ml - magnetic quantum number ml – determines permitted values of the z-component of the orbital angular momentum ml = 0, 1, 2, ... l Wave functions n=1 l=0 n,l,m n=2 r , , = Rnl r l ,m ( ) m ( ) l l l = 0,1 R( r ) ~ e r polynomial ~ e i l = 1 m = ±1 n=3 l = 0,1,2 Quantum number notation Degeneracy : one energy level En has different quantum numbers l and ml l = 0 : s states n=1 K shell l = 1 : p states n=2 L shell l = 2 : d states n=3 M shell l = 3 : f states n=4 N shell l = 4 : g states n=5 O shell . . . . Electron states K 1s 2s L n =1 l = 0 & ml = 0 n=2 l = 0 & ml = 0 l = 1 & ml = 1 2p l = 1 & ml = 0 l = 1 & ml = 1 n=3 l = 0 & ml = 0 3s l = 1 & ml = 1 l = 1 & ml = 0 l = 1 & ml = 1 3p l = 2 & ml = 2 M l = 2 & ml = 1 l = 2 & ml = 0 l = 2 & ml = 1 l = 2 & ml = 2 3d S-states probability P-states probability Spin angular momentum and magnetic moment Electron posseses spin angular momentum Ls. With this momentum magnetic momentum is connected: e s = Ls me e s = ge Ls 2me where ge is the gyromagnetic ratio For free electron ge=2 Spin angular Własny momentmomentum pędu - spin and magnetic moment Allowed values of the spin angular momentum are quantized : Ls = s( s 1) spin quantum number s = ½ Ls = 3 2 The z – component of the spin angular momentum: Lsz = ms 1 2 ms = 1 2 To label completely the state of the electron in a hydrogen atom, 4 quantum numbers are need: name label magnitude Principal quantum number Orbital quantum number magnetic quantum number Spin quantum number n 1, 2, 3, ... l 0, 1, 2, ... n-1 ml ms od –l do +l ± 1/2 Many – electron atoms and the exclusion principle Central field approximation: - Electron is moving in the total electric field due to the nucleus and averaged – out cloud of all the other electrons. - There is a corresponding spherically symmetric potential – energy function U( r). Solving the Schrodinger equation the same 4 quantum numbers are obtained. However wave functions are different. Energy levels depend on both n and l. • In the ground state of a complex atom the electrons cannot all be in the lowest energy state. Pauli’s exclusion principle states that no two electrons can occupy the same quantum – mechanical state. That is, no two electrons in an atom can have the same values of all four quantum numbers (n, l, ml and ms ) Shells and orbitals n 1 shell K l orbital 0 s 2 L 0 s L 1 p M M M N N N N 0 1 2 0 1 2 3 s p d s p 3 4 d f Nmax - maximum number of electrons occupying given orbital Nmax 2 2 6 2 6 10 2 6 10 14 Shells K, L, M n 1 2 l 0 0 ml 0 0 3 1 -1 0 0 1 0 1 -1 0 2 1 -2 -1 0 1 2 ms N 2 8 18 N : number of allowed states state with ms = +1/2 state with ms = -1/2 Hund’s rule - electrons occupying given shell initially set up their spins paralelly carbon oxygen 1s22s22p2 1s22s22p4 The periodic table of elements Atoms of helium, lithium and sodium n =3, l = 0 3s n =2, l = 1 n =2, l = 1 2p n =2, l = 0 n =2, l = 0 n =2, l = 0 2s n =1, l = 0 n =1, l = 0 n =1, l = 0 1s Helium (Z = 2) Lithium(Z = 3) Sodium (Z= 11) Electron configuration – the occupying of orbitals 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2 4f14 5d10 6p6 7s2 6d10 5f14 K : 1s 2 3 p 6 4 s1 Ca : 3 p 6 4s 2 Sc : 3d 1 4 s 2 Ti : 3d 2 4 s 2 V: 3d 3 4 s 2 Cr : 3d 5 4 s1 Mn: 3d 5 4 s 2 Cu : 3d 10 4 s1 Total angular momentum - J J = L LS J = j j 1 Possible two magnitudes of j : J z = m j , j = l s or j = l-s m j = j, j 1,, j 1, j Example: l = 1, s = ½ j = 1 12 = 3 2 lub j = 1 12 = 1 2 m j = 23 , 12 , 12 , 23 lub m j = 12 , 12 j = 3/2 j = 1/2 NMR ( nuclear magnetic resonance) Like electrons, protons also posses magnetic moment due to orbital angular momentum and spin ( they are also spin-1/2 particles) angular momentum. Spin flip experiment: Protons, the nuclei of hydrogen atoms in the tissue under study, normally have random spin orientations. In the presence of a strong magnetic field, they become aligned with a component paralell to the field. A brief radio signal flips the spins; as their components reorient paralell to the field, they emit signals that are picked up by sensitive detectors. The differing magnetic environment in various regions permits reconstruction of an image showing the types of tissue present.