Download Lesson 104: Review of Complex Numbers, Subsets of the Real

Lesson 104:
Review of Complex Numbers,
Subsets of the Real Numbers,
Representing Repeating
Decimals as Fractions
We review complex numbers by remember
that this number
4/7 + √2i
Is a complex number written in standard form.
The real part is 4/7 and is written first. The
imaginary part is √2i and is written after the
real part. We often use the letters a and b to
designate the standard form of a complex
number by writing
a + bi
And say that a and b can be any real numbers.
Since zero is a real number, either a or b can
be zero. If b is 0, then only a is left, and thus,
4
¾
-5√2
-19/3
Are all complex numbers whose imaginary
parts are zero. If a is zero, then only the
imaginary part b remains. Thus, the
imaginary numbers
-√2i
4√2/3i
-3i
i
Are all complex numbers whose real part
equal zero.
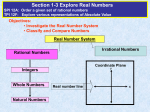
The set of real numbers has an infinite
number of members, and these can be used
to form an infinite number of subsets.
Normally, however, we restrict our attention
to five major subsets of the set of real
numbers.
The first three are:
 The counting (natural) numbers
 {1, 2, 3, …}
 The whole numbers
 {0, 1, 2, 3…}
 The integers
 {…-3, -2, -1, 0, 1, 2, 3…}
These three sets account for the numbers
that are designated when the number line is
drawn, because we usually designate the
location of the integers below a number line.
All integers can be written as fractions of
other integers. For example, -4, 0, and 13
can be written as fractions as shown here.
-4 = 12/-3
0 = 0/2
13 = -39/-3
We say that a number that can be written as
a fraction of integers is a rational number,
because ratio is another name for fraction.
The rest of the set of real numbers I made
up of all the positive numbers or arithmetic
and their negative counterparts. Some of
these numbers can be written as fractions of
integers and thus are rational numbers. The
rest cannot be written as fractions of integers
and are irrational numbers.
Irrational numbers cannot be
represented exactly with decimal
numerals that contain a finite number
of digits. The square root of 2 is an
irrational number and thus can only
be approximated with a decimal
numeral. A calculator gives an
approximation of the square root of 2
as
√2 = 1.4142136
The complete representation of this
number would require a numeral with an
infinite number of digits, and the digits
would occur in a nonrepeating pattern.
1. If the digits in a decimal numeral
terminate, the number is a rational
number.
2. If the digits in a nonterminating
decimal numeral repeat in a pattern,
the number is a rational number.
Example:
Show that 0.00314 is a rational
number by writing it as a fraction
of integers.
Answer:
314/100,000
Example:
Show that 0.00000623 is a rational
number by writing it as a fraction
of integers.
Answer:
623/100,000,000
We indicate that digits in a decimal
fraction repeat by drawing a bar over the
repeating digits. Thus, in the following
numerals, the digits under the bars
repeat in an endless pattern.
_____
 0.01623 = 0.01623232323…
_______
 1.0031543 = 1.0031543543543…
Each of these numerals represents a
rational number, and any rational
number can be written as a quotient of
integers. To write the first numeral as a
quotient of integers, we must get rid of
the repeating digits. We can eliminate
these repeating digits by subtracting the
number from the product of the number
and 100. this product has the same
repeating digits that the number has.
100N = 1.623 23 23 23
N = 0.016 23 23 23
99N = 1.607
(repeating digits eliminated)
The equation with 100N is the same as
the equation with N except that each
side has been multiplied by 100. we
multiplied by 100 because there were
two repeating digits. Three repeating
digits would require a multiplier of 1000,
four repeating digits would require a
multiplier of 10,000 etc. We will
investigate this procedure in the next
three examples.
Example:
____
Show that 0.01623 is a rational
number by writing it as a fraction
of integers.
Answer:
1607/99,000
Example:
_______
Show that 1.0031543 is a rational
number by writing it as a quotient
of integers.
Answer:
10,021,512/9,990,000
Example:
__
Show that 13.012 is a rational
number by writing it as a fraction
of integers.
Answer:
11,711/900
HW: Lesson 104 #1-30