Download 1.3 Exploring Real Numbers

1.3 Exploring Real Numbers
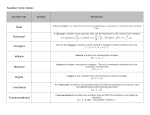
REAL NUMBERS
Rational Numbers (Q)
Integers (Z)
Whole Numbers (W)
Natural Numbers (N)
Irrational Numbers
Natural Numbers(N):
** counting numbers from 1,2,3,4,5,................
N = {1,2,3,4,5,................}
Whole Numbers (W):
** natural numbers including zero. They are 0,1,2,3,4,5,...............
W = {0,1,2,3,4,5,..............}
Integers (Z):
** Whole Numbers together with negative numbers.
** the positive numbers, 1, 2, 3, 4, ...., and negative
numbers,............-3, -2, -1, together with zero.
** Zero is neither positive nor negative, but is both.
Z = {..., -3, -2, -1, 0, 1, 2, 3, .....}
Rational Numbers (Q):
· All numbers of the form , where a and b are integers (but b
cannot be zero)
** numbers that can be written as a fraction and/or a
decimal that repeats or terminates
examples: 2, ½, - ¾, 0.5, 0.33
Irrational Numbers:
· Cannot be expressed as a fraction.
· As decimals they never repeat or terminate (rationals
always do one or the other)
** They go on forever
examples: √3, π, √5
Real Numbers (R):
** every number, irrational or rational.
REAL NUMBERS
0.45
Rational Numbers (Q)
4.5
2/3
-9
5.12
5/4
Integers (Z)
0
5
√9
3.1415926535...
π
Whole Numbers (W)
Natural Numbers (N)
Irrational Numbers
√7
Circle the set(s) of numbers that each example falls into:
1 Ra%onal Integers Whole Natural Irra%onal
½ Ra%onal Integers Whole Natural Irra%onal
0.4567893486…. Ra%onal Integers Whole Natural Irra%onal
-­‐4.5 Ra%onal Integers Whole Natural Irra%onal
√4 Ra%onal Integers Whole Natural Irra%onal
∏ Ra%onal Integers Whole Natural Irra%onal
-­‐3 Ra%onal Integers Whole Natural Irra%onal
√10 Ra%onal Integers Whole Natural Irra%onal
Name the set(s) of numbers to which each given number belongs.
1. -13
2. 3.28
3. 42
4.
5.
6.
Which set of numbers (natural, whole, integer, rational, irrational, or real)
is most appropriate for the given situations?
1. temperatures in Alaska
2. homework grades
3. shoe sizes
4. tablespoons of sugar used in recipes
5. pounds of sugar bought at the store
It is the number of units (distance) from zero.
There are different ways to order rational
numbers ...
one way is to change all the numbers to decimals to find the
least to greatest numbers:
OR...
You can compare the rational numbers using cross
multiplication...
Comparison Property
for
Rational Numbers:
a
c
For any rational numbers
/ b and
/ d, with b > 0 and d > 0:
a
c
1. if / b < / d, then ad < bc
and
a
c
b
2. if ad< bc, then / < / d.
this property holds true for all signs:
<, >, <, >, or =.
What does that mean???
if you cross multiply your denominator on the left with your
numerator on your right, and vice versa... the larger product is
the larger rational number.
3
Use the property to compare
Cross Multiply:
3 4
?
8 1
3(11) ? 8(4)
33 ? 32
33 > 32
therefore...
3
4
/ 8 > / 11
/8
4
and / 11
1.3 p20: 1-10, 14-23, 28-41e, 57 - 73e,